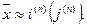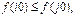Известно, что мировой объем выпуска персональных компьютеров за последние двадцать лет с достаточной степенью точности описывается обыкновенным дифференциальным уравнением первого порядка

Y¢(t) = 2tY(t)

Требуется найти численное решение данного дифференциального уравнения с заданными начальными условиями (задача Коши) Y_t=0 = 1 млн. шт.

Задачу решить:

· методом Эйлера Y1(t);

· методом Эйлера-Коши Y2(t);

· с использованием формулы Тейлора второго порядка точности Y3(t).

Сравнить полученные решения с точным (аналитическим) Y(t)=exp(t²) графическим способом и с помощью полученных числовых значений для значений tот0 до 2 (за единицу измерения времени t принято 10 лет).

4.2. Расчетные формулы

Метод Эйлера

Расчетная формула

Y_i+1 = Y_i + h × f(t_i,Y_i),

где h – шаг численного решения (h=0.01),

а f(t_i,Y_i) = Y¢ = 2tY.

Метод Эйлера-Коши

Расчетная формула

Y_i+1 = Y_i + h/2 × (f(t_i,Y_i) + f(t_i+1, Y_i + h × f(t_i,Y_i))).

где h – шаг численного решения (h=0.01),

Использование формулы Тейлора второго порядка точности

Расчетная формула

Y_i+1 = Y_i + h × Y¢(t) + h²/2× Y¢¢(t),

где h – шаг численного решения (h=0.01).

Дифференцируя исходное уравнение по t, получим следующее выражение для второй производной:

Y¢¢ = 2Y + 2t Y¢ = 2(1 + 2t²) Y

И окончательно расчетная формула примет вид

Y_i+1 = Y_i + h2t_iY_i + h²/2× 2(1 + 2t_i²) Y_i =

= (1 + 2t_i h + (1 + 2t_i²) h²) Y_i.

4.3. Результаты расчета

В результате выполнения работы должны быть представлены графики трех кривых численного решения (разными методами) данного дифференциального уравнения и кривая аналитического решения;

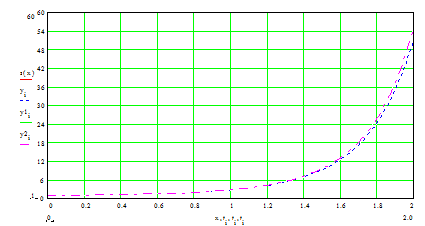
Рис. 4.1

4.4. Исследование значения величины шага на точность численного решения

На примере численного решения методом Эйлера провести анализ влияния уменьшения шага h = 0.1, 0.01, 0.001 на значение абсолютной погрешности, сделать выводы по работе.

В результате выполнения данного пункта должны быть представлены три кривых численного решения с разным шагом, иллюстрирующие точность численного решения в зависимости от величины шага.

Рис. 4.2

4.5. Сделать выводы по работе

Лабораторная работа 5

МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ.

МЕТОД ЗОЛОТОГО СЕЧЕНИЯ

Цель работы:

Практическая реализация алгоритма одномерной оптимизации (минимизации) с использованием правила золотого сечения. Знакомство с основными принципами минимизации.

Время выполнения работы 4 часа.

5.1. Индивидуальное задание

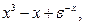Для заданной функции y(x)

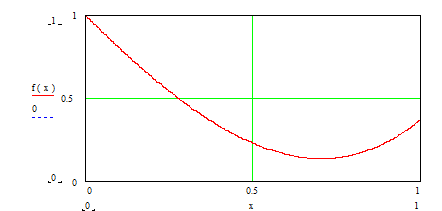
c точностью до 0.1 найти точку x локального минимума функции, локализованной на отрезке [0,1].

Рис. 5.1

Проверить найденное решение графическим способом и через нахождение экстремума с вычислением первой производной.

Принцип золотого сечения

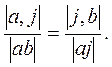Основной принцип золотого сечения отражен в следующемсоотношении:

Рис.5.2

Это правило положено в основу уменьшения отрезка локализации.

Рис.5.3

Исходный отрезок [a0,b0], на котором ищется решение, разбивается двумя точками i0 и j0 по правилу золотого сечения:

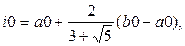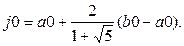Правило локализации (уменьшения отрезка) следующее:

если		то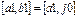
если		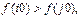то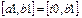

В MathCADе данное правило записывается следующим образом:

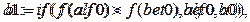
Это иллюстрирует следующий рисунок.

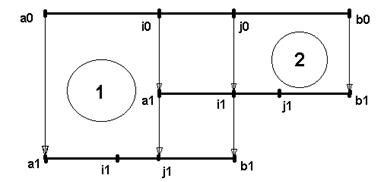
Рис.5.4

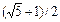Для нахождения точки локального минимума x с заданной точностью необходимо проделать n итераций. Каждая итерация сокращает длину отрезка локализации в раз. Поэтому

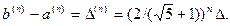Оценка погрешности определяется:

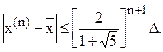При достижении заданной точности (e<0.1) итерации следует прекратить и положить