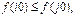Выполнение расчетов с использованием пакета программ mathcad

ВЫПОЛНЕНИЕ РАСЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПАКЕТА ПРОГРАММ MATHCAD

Цель работы:

Приобретение практических навыков решения трансцендентных уравне­ний, операций над матрицами, вычисления определенных интегралов, пошаговых значений функций, производных и построение графиков в среде па­кета MathCAD.

Индивидуальное задание

p1 – последняя цифра в зачетной книжке студента;

р2– предпоследняя цифра в зачетной книжке студента;

р3 – число букв в фамилии студента.

Постановка задачи

На лесной опытной станции были произведены 20 измерений диаметра дерева D на высоте груди (1.3м) и высоты H. Результаты измерений сведены в таблицуТребуется решить задачу интерполяции – для любого значения из интервала от Dmin до Dmax найти значение высоты H.

Интерполяция кубическими сплайнами

Интерполяция кубическими сплайнами состоит в сглаживании кривой так, что первая и вторая производные сглаживаемой кривой являются непрерывными. Искомая кривая определяется рядом соединенных отрезков кубических функций. Интерполяция осуществляется в 3 этапа:

1. Исходные данные требуется представить в виде матрицы, где каждый из двух столбцов - это вектор значений D_i и H_i. Затем, используя функцию V=csort(M,N),отсортировать значения матрицы по столбцу Di в порядке возрастания. В данном формате функции csort(M,N) M– обозначение матрицы, N– номер столбца, по которому производится сортировка.

1. 
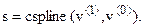
   Использование функции s=cspline(x,y) на векторах x и y возвращает вектор s, содержащий значения вторых производных сглаживаемой кривой в заданных точках. В качестве векторов x и yследует задатьзначения D_i и H_i, что соответствует столбцам V<0>и V<1>:

1. Использование функции interpпозволяет найти значения функции q(z) для промежуточных значений zиз интервала от Dmin до Dmax:

q(z)=interp(s,x,y,z)

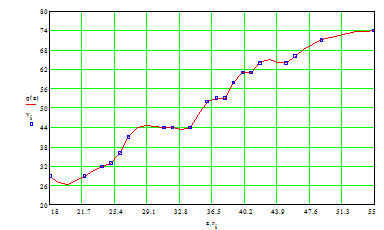
Рис. 3.1

В результате интерполяции кубическими сплайнами должен быть представлен интерполяционный график, состоящий из точечного графика исходных значений диаметра и высоты дерева и гладкой интерполяционной кривой, проходящей через данные точки.

Приближение функции с использованием метода наименьших квадратов

Время выполнения работы 4 часа.

4.1. Индивидуальное задание

Известно, что мировой объем выпуска персональных компьютеров за последние двадцать лет с достаточной степенью точности описывается обыкновенным дифференциальным уравнением первого порядка

Y¢(t) = 2tY(t)

Требуется найти численное решение данного дифференциального уравнения с заданными начальными условиями (задача Коши) Y_t=0 = 1 млн. шт.

Задачу решить:

· методом Эйлера Y1(t);

· методом Эйлера-Коши Y2(t);

· с использованием формулы Тейлора второго порядка точности Y3(t).

Сравнить полученные решения с точным (аналитическим) Y(t)=exp(t²) графическим способом и с помощью полученных числовых значений для значений tот0 до 2 (за единицу измерения времени t принято 10 лет).

4.2. Расчетные формулы

Метод Эйлера

Расчетная формула

Y_i+1 = Y_i + h × f(t_i,Y_i),

где h – шаг численного решения (h=0.01),

а f(t_i,Y_i) = Y¢ = 2tY.

Метод Эйлера-Коши

Расчетная формула

Y_i+1 = Y_i + h/2 × (f(t_i,Y_i) + f(t_i+1, Y_i + h × f(t_i,Y_i))).

где h – шаг численного решения (h=0.01),

Использование формулы Тейлора второго порядка точности

Расчетная формула

Y_i+1 = Y_i + h × Y¢(t) + h²/2× Y¢¢(t),

где h – шаг численного решения (h=0.01).

Дифференцируя исходное уравнение по t, получим следующее выражение для второй производной:

Y¢¢ = 2Y + 2t Y¢ = 2(1 + 2t²) Y

Принцип золотого сечения

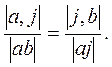Основной принцип золотого сечения отражен в следующемсоотношении:

Рис.5.2

Это правило положено в основу уменьшения отрезка локализации.

Рис.5.3

Исходный отрезок [a0,b0], на котором ищется решение, разбивается двумя точками i0 и j0 по правилу золотого сечения:

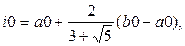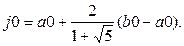Правило локализации (уменьшения отрезка) следующее:

если		то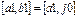
если		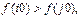то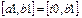

В MathCADе данное правило записывается следующим образом:

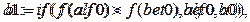
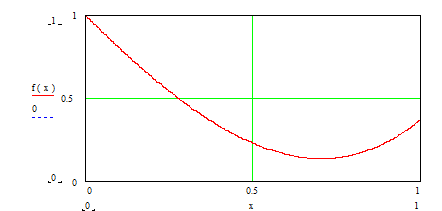
Это иллюстрирует следующий рисунок.

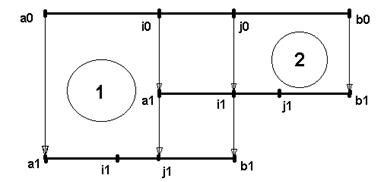
Рис.5.4

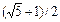Для нахождения точки локального минимума x с заданной точностью необходимо проделать n итераций. Каждая итерация сокращает длину отрезка локализации в раз. Поэтому

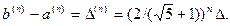Оценка погрешности определяется:

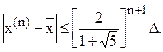При достижении заданной точности (e<0.1) итерации следует прекратить и положить

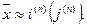
ВЫПОЛНЕНИЕ РАСЧЕТОВ С ИСПОЛЬЗОВАНИЕМ ПАКЕТА ПРОГРАММ MATHCAD

Цель работы:

Приобретение практических навыков решения трансцендентных уравне­ний, операций над матрицами, вычисления определенных интегралов, пошаговых значений функций, производных и построение графиков в среде па­кета MathCAD.

Индивидуальное задание

p1 – последняя цифра в зачетной книжке студента;

р2– предпоследняя цифра в зачетной книжке студента;

р3 – число букв в фамилии студента.