Определение приведенного момента движущих сил

Работа сил сопротивления известна, рассмотрим режим установившегося движения, т. е. работа движущих сил и работа сил сопротивления в начале и в конце цикла одинаковы. Полученную ординату в 16-м положении У_д =У_с откладываем вверх. Условно принимаем, что М_д =const, значит работа движущих сил представляет собой наклонную прямую, соединяющую начало цикла с У_с .

Графически проинтегрируем А_С , получим М_С.

М_С =У_д = 95,16 Нм

3.7. Приведенный момент инерции механизма

Вычислим приведенный момент инерции механизма по равенству кинетических энергий приведенного момента и приводных масс и моментов инерции звеньев механизма. Построим график , приняв масштабные коэффициенты и .

Вычислим приведенный момент инерции для одного оборота начального звена, поскольку для второго оборота значения будут такими же:

откуда

Вычисление для всех положений показаны в табл. 3.5.

Таблица 3.5.

Приведенные моменты инерции звеньев

Параметры	Номера положений
0,8	1,9	2,1	3,11	4,12	5,13	6,14	7,15	8,16
S s2, мм	0,0236603	0,030337	0,03381	0,028064	0,02366	0,028049	0,03381	0,030351	0,02366
m2, кг	1,4	1,4	1,4	1,4	1,4	1,4	1,4	1,4	1,4
	0,0007837	0,001288	0,0016	0,001103	0,000784	0,001101	0,0016	0,00129	0,000784
Ψ2	0,2632376	0,189652		0,189729	0,263238	0,189652		0,189729	0,263238
J2, кгм2	0,08	0,08	0,08	0,08	0,08	0,08	0,08	0,08	0,08
	0,0055435	0,002877		0,00288	0,005544	0,002877		0,00288	0,005544
S s3, м/с		0,028566	0,03381	0,019257		0,019247	0,03381	0,02858
m3, кг	0,95	0,95	0,95	0,95	0,95	0,95	0,95	0,95	0,95
		0,000775	0,001086	0,000352		0,000352	0,001086	0,000776
S s4, м/с	0,0236603	0,028049	0,03381	0,030356	0,02366	0,030337	0,03381	0,028064	0,02366
m4, кг	1,4	1,4	1,4	1,4	1,4	1,4	1,4	1,4	1,4
	0,0007837	0,001101	0,0016	0,00129	0,000784	0,001288	0,0016	0,001103	0,000784
ψ4	0,2632376	0,189652		0,189729	0,263238	0,189652		0,189729	0,263238
J4, кгм2	0,08	0,08	0,08	0,08	0,08	0,08	0,08	0,08	0,08
	0,0055435	0,002877		0,00288	0,005544	0,002877		0,00288	0,005544
S s5, м/с		0,019247	0,03381	0,02858		0,028566	0,03381	0,019257
m5, кг	0,95	0,95	0,95	0,95	0,95	0,95	0,95	0,95	0,95
		0,000352	0,001086	0,000776		0,000775	0,001086	0,000352
Jпр, кгм2	0,0126545	0,009272	0,005373	0,009281	0,012655	0,009272	0,005373	0,00928	0,012655
ΔJпр	0,0072818	0,003899		0,003908	0,007282	0,003899		0,003907	0,007282
YΔJпр, мм	66,866759	35,80482		35,88419	66,86676	35,80482		35,88035	66,86676

Построим график = , предварительно определив масштабные коэффициенты:

3.8. Определение момента инерции маховика

Построим диаграмму Витенбауэра , исключив параметр из графиков и . К кривой Витенбауэра проведем касательные под углами и к оси , которые определяются из уравнений:

Для удобства построения диаграммы графики и = разместим так, как показано на листе приложения 1.

Теперь легко графически исключить параметр .

Вычислим углы и

где - допустимое значение коэффициенту неравномерности движения механизма.

Момент инерции маховика вычислим по формуле:

где |ab| - отрезок на оси ординат , которые отсекают касательные к кривой Витенбауєра.

Проведем касательные к кривої и замерим отрезок .

Получим = 130,41 мм.

Вычислим по зависимости:

Маховики изготовляются из стали или чугуна в виде диска или в виде обода со спицами и ступицей (рис. 3.1).

Диаметр маховика в виде диска определяется зависимостью:

где - плотность материала, кг/м ; - отношение ширины маховика B к его диаметру D. Выберем маховик в виде диска и вычислим его размеры:

где - плотность стали, 0,2.

Масса маховика:

Динамический анализ механизма

Определение закона движения начального звена

Для определения угловой скорости начального звена воспользуемся кривой 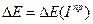и формулой:

,

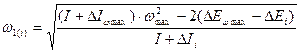где: I = 0,1949 кг*м² – момент инерции на начальном звене;

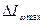- момент инерции в точке, в которой угловая скорость максимальна;

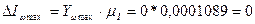кг*м².

.

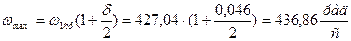Определим постоянные величины.

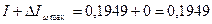кг*м²

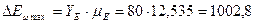Дж.

Определим угловую скорость для положения 1’

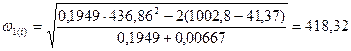рад/с.

Значения угловой скорости представлены в таблице 4.1.

Угловое ускорение начального звена определяется по формуле:

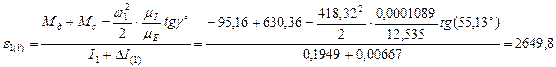рад/с².

Проверим 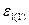по формуле:

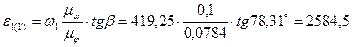рад/с².