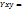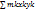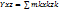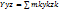Методика решения задач статики

Целью большенства задач статики является нахождение неизвестных сил приложенных к уравновешенной конструкции этим силам обычно являются реакции связей:

1,Выбираем тело равновесия которого будем рассматривать

2,Изображаем силы приложенные к телу

3,Классификации систему сил и определяем число уравнений равновесия

4,Сопоставляем число неизвестных сил и число уравнений равновесия, делаем вывод по статической определимости системы. В случае статической неопределимости разбиваем конструкцию на части и рассматриваем равновесие отдельных частей.

5,Вводим систему координат

6,Записываем уравнения равновесия

7,Находим не известные силы.

Равновесие системы тел.

Определение внутренних сил.

Системой тел называется совокупность нескольких тел соединенных между собой шарнирами, нитями и т.д.

(РИСУНОК)

Рассмотри равновесие конструкций состоящих из 2-ух частей соединенных шарниром через шарниром правая часть конструкции воздействует на левую часть силой Rс по аксиоме действия и противодействия, левая часть конструкции воздействует на правую часть с силой Rc’. Если рассматривать равновесие конструкции в целом то внутренние силы Rс и Rc’ не могут быть найдены из уравнения равновесия. Соответствующие слогаемые сокращаются и число внешних сил Rax, Ray, Rbx , Кин превышает число уравнений равновесия левой части конструкций с учетом от брошенной правой части.

(РИСУНОК)

Затем рассмотрим равновесие правой части конструкции с учетом воздействия отброшенной левой части.

(РИСУНОК)

Внутренние силы при этом в уравнениях не сокращаются и при этом смогут быть определенны число уравнений возрастает до 6, что соответствует числу не известных сил, система становится статически определенной.

Центр тяжести

(РИСУНОК)

Пусть тело находиться в гравитационном поле земли, разобьем его на несколько частей и приложим к каждой части соответствующую силу тяжести силы Р1,Р2,Рn образуют пространственную систему перпендикулярных сил. Найдем равнодействующую этих системы сил т.е. модуль этой силы и точку приложения. Модуль равнодействующей определяется по формуле:

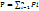(1)

Модуль силы определяется по формуле называется весом тела. Положение точки приложения силы определяется по формуле:

rc= 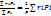(2)

Положение точки С относительно к телу не зависит от ориентации тела в гравитационном поле. Геометрическая связь с телом т.е. точкой через которую проходит равнодействующая силы тяжести частиц тела при любой его ориентации в любом поле называется центром тяжести тела. Проецируя уравнения 2 на оси координат получим координаты центра тяжести:

Xc=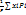

yc= 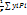(3)

zc=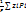

Тело называется однородным если его плоскость по всему объему тела постоянна:

Pi=ρ*Vi (4)

ρ-удельный вес

Vi-Объем I частицы весом Pi

Для однородных тел ρ=const (5)

Преобразуем формулу (3)

Xc=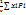

yc= 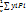(6), Где V=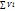

zc=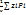

Из уравнения (6) следует, что положение центра тяжести не зависит от материала из которого изготовленно тело, а определяется лишь формой тела. Поэтому точку определяемую по уравнениям (6) называют центром тяжести объема. Для пластины постоянной толщины получим:

Xc=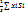

yc= 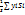(7)S- площадь всей пластины.

Точку определяемую по формуле (7) называют центром тяжести площади.

Способы определения положения центра тяжести.

Существует следующие способы: 1) использование симметрии

2) разбиение 3) экспериментальный

Способы используются для однородных тел.

1,Использование симметрии : если тело имеет плоскость, ось или центр симметрии то центр тяжести находиться в плоскости на оси или в центре симметрии. (РИСУНОК)

2,Разбиение: если тело удастся разбить на части положения, центров тяжести которых заранее известны то можно использовать формулы:

Xc= 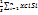, (8), N-число частей на которое разбито тело.

yc= 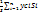, yci- координаты центров тяжести

Способ разбития можно распространить на тела имеющие вырезы, при этом площадь вырезом условно считается отрицательной.(РИСУНКИ)

Трение-скольжение

При стремлении передвинуть тело по шероховатости поверхности возникает трение скольжения.(РИСУНОК)

Предельная сила трения скольжения определяется по формуле :

Fпр=f*N

Величина этого коэфицента зависит от материала и состояния соприкасающихся частей. Если тело начало передвигаться по шероховатой поверхности то величина силы трения скольжения определяется

Fтр=f*N

Его величина зависит от материала, состояния соприкасающихся частей и в малой степени зависит от скорости тела.(РИСУНОК)

При решении задач с четом трения скольжения обычно рассматривают предельный случай равновесия. В этом случае сила трения скольжения достигает своего предельного значения.

Сила трения-качения

Трение качение называется сопротивление возникающие при качании одного тела по поверхности другого. Рассмотрим круглый цилиндрический каток радиусом R и весом P лежащий на горизонтальной шероховатой поверхности(РИСУНОК)

На рис 91) изображен идиальный случай, когда каток не деформирует поверхность качения обеспечивается парой сил F и Fтр. При любой какой угодно малой силе F. На рис (2) изображен реальный случай когда поверхность деформируется. При этом сила N смещается относительно осей симметрии на величину К. Возникает пара сил P и N. Препятствующая качению катка. Плечо этой пары называется коэфициентом трения-качения. Условием при котором обеспечивается качением катка записывается следующим образом(РИСУНОК)

Теорема Гюгенса

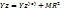Момент инерции тела относительно оси равен моменту инерции тела оси параллельной данной оси и проходящих через центр масс тела сложенной с произведением массы тела на квадрат расстояния между осями. Ось проходящая через центр масс называется центральной. Центробежные моменты системы определяются: