При плоском косом изгибе направление полного прогиба перпендикулярно к нулевой линии.

7. Три типа задач расчета конструкций на прочность |при косом изгибе.

8.

1. Поверочный расчет - проверка прочности;

2. Проектный расчет или проектировочный расчет - подбор сечения [определить W_x(размеры сечения), при заданном отношении W_x/W_y];

3. Определение грузоподъемности - проверка по несущей способности (определить M).

Порядок проверки прочности балки, работающей в условиях косого или пространственного изгиба, тот же, что и для балки, работающей при плоском поперечном изгибе.

Для этого необходимо:

- построить эпюры внутренних усилий (изгибающих моментов).

Для построения эпюр внутренних усилий раскладываем нагрузки на вертикальную и горизонтальную составляющие.

- выбрать опасные сечения – это сечения, где имеет место наиболее неблагоприятное сочетание изгибающих моментов;

- в опасных сечениях найти опасные точки – точки с максимальными нормальными напряжениями;

- записать условие прочности в этих точках.

Из условия прочности либо подобрать размеры поперечного сечения, либо найти допускаемую нагрузку, либо просто сделать вывод о возможности безопасной эксплуатации конструкции.

Пример 1.

Подобрать прямоугольное сечение балки при условии, что h = 2b,[σ]= 160 МПа P= 60кН, α =30 ͦ, ℓ=2,8 м..

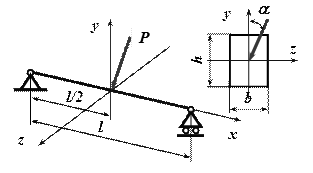
Решение:

Разложив силу P на две составляющие, действующие по нап­равлению главных осей поперечного сечения балки, определяем опорные реакции и строим эпюры изгибающих моментов M_z и M_y . Наибольшие моменты действуют в среднем сечении, где

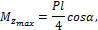
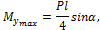
следовательно, это сечение является опасным.

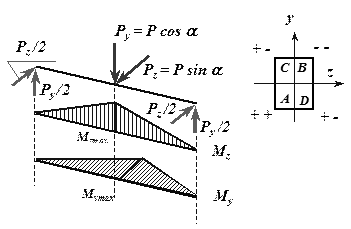
Эпюры изгибающих моментов к примеру 1

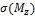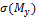Для определения положения опасной точки расставим знаки от и в угловых точках поперечного сечения балки. При действии момента 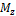в точках A и D будут иметь место положительные (растя­гивающие) напряжения, а в точках C и B - отрицательные (сжимающие) напряжения. При действии момента 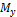в точках A и C будут иметь место положительные 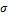, а в точках B и D - отрицательные. Точки поперечного сечения A и B, в которых действуют нормальные напряжения одного знака, являются опасными; для них и должны составляться условия прочности.

Судя по условию задачи, материал, из которого изготовлена балка, является пластичным ( 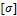=160 МПа) и, следовательно, одинаково сопротивляется деформации растяжения и деформации сжатия. Таким образом, точки A и B являются равноопасными, и для них используется одно условие прочности

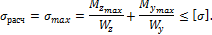
Вычислим моменты сопротивления сечения при заданном соотношении высоты и ширины

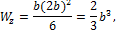
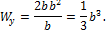
Подставляя в условие прочности выражения для изгибающих моментов и моментов сопротивления, получим:

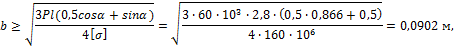
тогда h = 2b = 18,04 см.

Пример 2.

При установке на опоры двутавровой балки (№ 60: 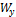=182 см³, 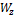=2560 см³), предназначенной для работы на изгиб в верти­кальной плоскости, совпадающей с плоскостью стенки, была допущена ошибка и стенка двутавра отклонилась от вертикали на угол 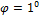. Определить связанное с этим увеличение наибольших нормальных напряжений.

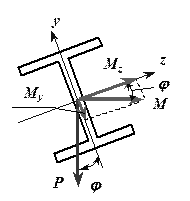
Появление внутренних изгибающих моментов

при косом изгибе.

Решение:

Отклонение оси двутавра (ось y) от вертикали привело к возникновению косого изгиба и появлению изгибающих моментов 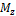и .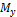

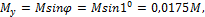
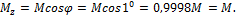
Максимальные напряжения при косом изгибе

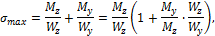
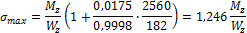
так как 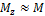, то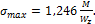

В случае правильной установки балки, сила P совпадала бы с вертикальной осью балки y, и имел бы место прямой изгиб, изгибающий момент был бы равен M , а напряжения

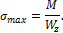
Таким образом, максимальные напряжения при косом изгибе за счет такого незначительного отклонения от вертикали возрастут на 24,6 %.