Алгоритм геометрического метода решения задач ЛП.

Решение задач ЛП геометрическим методом осуществляется по следующему алгоритму:

1.Строим координатные оси Х1ОХ2 и с учетом коэффициентов математической модели выбираем масштаб.

2.Находим область допустимых решений (ОДР) системы ограничений математической модели

3.Строим прямую целевой функции и показываем направление наискорейшего ее изменения (нормаль-gradL).

4.Линию целевой функции (линия уровня) перемещаем по направлению нормали для задач на максимум целевой функции и в противоположном направлении - для задач на минимум ЦФ.

Перемещение линии уровня через ОДР производится до тех пор, пока у нее окажется только одна общая точка с областью допустимых решений. Эта точка будет точкой экстремума, и будет определять единственное решение задачи ЛП.

Если окажется, что линия уровня совпадает с одной из сторон ОДР, то задача ЛП будет иметь бесчисленное множество решений.

Если ОДР представляет неограниченную область, то целевая функция – неограниченна.

Задача ЛП может быть неразрешима ,когда определяющие ее ограничения окажутся противоречивыми.

5.Находим координаты точки экстремума и значение ЦФ в ней.

Пример:

Торговая фирма для продажи товара трех видов использует ресурсы: время и площадь торговых залов. Затраты ресурсов на продажу одной партии товаров каждого вида даны в таблице. Прибыль получаемая от реализации одной парии товаров 1 вида – 5 у.е. 2 вида – 8 у.е.

Определить оптимальную структуру товарооборота, обеспечивающую фирме максимальную прибыль.

Решение задачи.

Математическая модель прямой задачи

Max Z= 5x₁+8x₂

0,5 x₁+0,7x₂ £ 370

0,1 x₁+0,3x₂ £ 90

x_1,2 ³ 0

Математическая модель двойственной задачи

Min Z’= 370y₁+90y₂

0,5y₁+0,1y₂ ³ 5

0,7у₁+0,3у₂ ³ 8

y₁,₂ ³ 0

Разберем экономический смысл переменных, входящих в модели и ограничений, составленных на основе условия задачи.

x₁ – количество товара первого вида, которое необходимо продавать согласно оптимальному плану.

х₂ – количество товара второго вида, которое необходимо продавать согласно оптимальному плану.

0,5 x₁+0,7x₂ – это условие показывает, сколько времени всего будет потрачено на продажу товаров первого и второго вида.

0,1 x₁+0,3x₂ – это условие показывает, сколько площади будет потрачено на продажу товаров первого и второго вида.

5x₁+8x₂ – выручка, полученная при продаже оптимального количества товаров первого и второго вида.

у₁ – цена одной единицы первого ресурса (1 часа работы продавца)

у₂ – цена одной единицы второго ресурса (1 м² площади торгового зала).

0,5y₁+0,1y₂ – это условие показывает, сколько всего денежных единиц будет потрачено на продажу изделий первого вида.

0,7у₁+0,3у₂ это условие показывает, сколько всего денежных единиц будет потрачено на продажу изделий второго вида.

370y₁+90y₂ – это условие показывает, сколько всего денежных единиц будет потрачено на продажу изделий первого и второго вида.

Непосредственное решение состоит из построения нескольких прямых на плоскости XOY. Построение неравенств на плоскости состоит из построения соответствующих прямых и выбора нужной полуплоскости. Для выбора полуплоскости необходимо подставить какую-нибудь точку плоскости (чаще всего точку (0,0)) в соответствующее неравенство и о выполнении или невыполнении этого неравенства сделать вывод о том, какая именно полуплоскость соответствует неравенству.

Для построения прямых достаточно взять две точки.

Целевая функция приравнивается к 0 для возможности ее построения. Потом с помощью параллельного переноса функция цели двигается так, чтобы из положения секущей она стала касательной. В точке, где целевая функция становится касательной области допустимых значений и будет точка оптимального решения.

Построение системы ограничений для данной задачи дает следующую область ограничений.

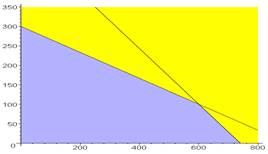
Темным цветом показана область допустимых значений. Теперь, если построить целевую функцию на этом же графике, то видно, что при параллельном переносе из точки (0,0) она становится касательной в точке (600,100).

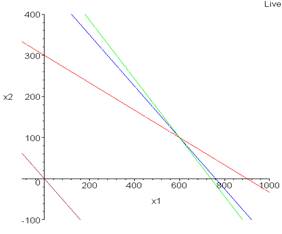
Аналитически найдем координаты точки пересечения двух прямых системы ограничений.

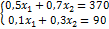
Решая эту систему, получаем, что для получения максимальной прибыли необходимо продавать 600 единиц товара первого вида и 100 товара второго вида. При этом максимальная выручка от продажи составит 600*5+100*8=3800 ден. ед.

Решение задачи ЛП в MathCAD

В Mathcad к классу задач линейного программирования относятся задачи, в которых требуется оптимизировать (определить максимум или минимум) целевую функцию вида:

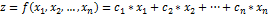
при следующих ограничениях:

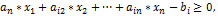
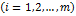
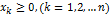
Одним из способов решение подобных задач в Mathcad является использование блока given с функциями minimize и maximize .

Функции Minimize и Maximize, которые могут быть использованы как сами по себе, так и совместно с блоком given. Аргументы функций: имя функции, экстремум которой ищется, и список ее аргументов.

- Minimize (y,x) - для отыскания значения х, соответствующего локальному минимуму функции у(х);

- Maximize (y,x) - для отыскания значения х, соответствующего локальному максимуму функции у(х).

Так как у(х) может иметь несколько локальных экстремумов, а функции Minimize (y,x) и Maximize (y,x) позволяет найти только одно значение, то в Mathcad дополнительно задается начальное приближение переменной х. В результате находится значение экстремума функции y(x), ближайшее к заданному начальному приближению переменной х.

В качестве примера рассмотрим задачу планирования производства красок.

Суть задачи в следующем. Фабрика выпускает два типа красок - I и Е. Для производства красок используются два компонента - А и В. Максимальные суточные запасы этих компонентов: компонент А - 6 тонн; компонент В – 8 тонн. Расходы компонентов А и В на производство 1 тонны краски следующие: для краски I - A/B= 2/1; для краски Е - А/В = 1/2. Суточный спрос на краску I никогда не превышает спрос на краску Е более, чем на 1 тонну. Спрос на краску I никогда не превышает 2 тонн в сутки. Оптовые цены на краску I – 2000 рублей за тонну, а на краску Е – 3000 рублей за тонну. Определить максимальный доход фабрики от продажи краски. Обозначив суточный объем выпуска краски I за x1, а суточный объем выпуска краски Е за х2, получаем экономико - математическую модель задачи, вид которой представлен ниже:

Решение задачи ЛП в MatLAB

В среде MATLAB задачи линейного программирования решаются с помощью функции linprog.

Функция linprog решает задачу линейного программирования в форме:

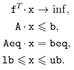
Основными входными данными linprog являются: вектор коэффициентов целевой функции f, матрица ограничений-неравенств A, вектор правых частей ограничений-неравенств b, матрица ограничений-равенств Aeq, вектор правых частей ограничений-равенств beq, вектор lb, ограничивающий план x снизу, вектор ub, ограничивающий план x сверху. На выходе функция linprog даёт оптимальный план x задачи (1) и экстремальное значение целевой функции fval.

Пример: Решим в MATLAB задачу линейного программирования:

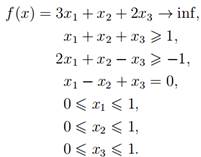
Соответствующая программа (m-файл)∗ выглядит так:

clear all

close all

clc % удаляются все текущие переменные из памяти MATLAB, закрываются все графические окна, очищается экран консоли

C = [3 1 2]; % задаётся вектор длины три

D = [1 1 1; 2 1 -1]; % строки матрицы разделяются точкой с запятой

B = [1 -1];

Aeq = [1 -1 1];

beq = [0];

lb = zeros(3,1); % задаётся нулевой вектор длины три

ub = [1 1 1];

f = C;

A = -D;

b = -B; % появляются знаки «-», так как ограничения-неравенства

Dx > B приводятся к виду −Dx 6 −B

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub);

x

fval

Запустив программу, получим сообщение

Optimization terminated.

x =

0.5000

0.5000

fval =

1.5000

Дополнительно можно задать начальное приближение x0:

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub,x0).

Если какой-то из входных параметров отсутствует, на его место следует поставить квадратные скобки [], за исключением случая, когда это последний параметр в списке. Например, если нужно решить задачу без ограничений-равенств, в которой не задано начальное приближение, то оператор вызова функции linprog будет выглядеть так: [x,fval] = linprog(f,A,b,[],[],lb,ub).

(Квадратные скобки в конце списка, соответствующие начальному приближению, не ставятся.) С помощью входного параметра options устанавливаются некоторые дополнительные настройки, в частности, выбирается алгоритм решения. MATLAB решает задачи линейного программирования двумя способами: алгоритмом внутренней точки (Large-Scale Algorithm) и вариантом симплекс-метода (Medium-Scale Algorithm). По умолчанию используется алгоритм внутренней точки. Чтобы выбрать симплекс-метод, нужно написать options = optimset(’LargeScale’,’off’,’Simplex’,’on’);

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub,[],options).

MATLAB позволяет выводить информацию о том, как завершилось решение задачи. За это отвечает параметр exitflag. Если значение exitflag равно 1, то найдено решение задачи, если равно 0, то превышено допустимое число итераций, если равно −2 — множество планов задачи пусто, если равно −3 — целевая функция не ограничена снизу на множестве планов. Интерпретация других значений параметра exitflag приведена в MATLAB Help. Для симплекс-метода допустимое число итераций (MaxIter) по умолчанию в 10 раз больше количества переменных. Значение MaxIter можно изменить. Чтобы установить допустимое число итераций равным, к примеру, 10, нужно написать

options =

optimset(’LargeScale’,’off’,’Simplex’,’on’,’MaxIter’,10);

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub,[],options).

Если после выполнения десятой итерации решение не будет найдено, параметр exitflag станет нулевым и на экране появится сообщение

Maximum number of iterations exceeded;

increase options.MaxIter.

Параметр output содержит информацию о процессе оптимизации, в частности, число итераций (iterations) и используемый алгоритм (algorithm).

Другие поля параметра output описаны в MATLAB Help. Запустим с данными из примера 1 следующую программу:

options = optimset(’LargeScale’,’off’,’Simplex’,’on’);

[x,fval,exitflag,output] =

linprog(f,A,b,Aeq,beq,lb,ub,[],options);

exitflag

output.iterations

output.algorithm

На выходе получим:

Optimization terminated.

exitflag =

ans =

ans =

medium scale: simplex

Это означает, что симплекс-метод успешно завершил работу, для нахождения решения потребовалось одна итерация. Наконец, в выходном параметре lambda содержится решение двойственной задачи линейного программирования. Параметр lambda состоит из четырёх массивов: lambda.ineqlin, lambda.eqlin, lambda.upper, lambda.lower. В этих массивах находятся двойственные переменные, приписанные ограничениям-неравенствам, ограничениям-равенствам, ограничениям на план сверху и снизу соответственно.

Пример: Решим в MATLAB задачу линейного программирования:

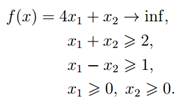
Соответствующая программа будет выглядеть так:

clear all

close all

clc

C = [4 1];

D = [1 1; 1 -1];

B = [2 1];

lb = zeros(2,1);

f = C;

A = -D;

b = -B;

options = optimset(’LargeScale’,’off’,’Simplex’,’on’)};

[x,fval,exitflag] = linprog(f,A,b,[],[],lb,[],[],options);

x

fval

exitflag

В результате работы программы получим:

Optimization terminated.

x =

1.5000

0.5000

fval =

6.5000

exitflag =