Методы Рунге–Кутты. «Подводные камни»

Следует иметь в виду, что даже если ошибка ограничения мала, все равно метод Рунге–Кутты может при неблагоприятных условиях дать совершенно ошибочные результаты.

Малые ошибки (ограничения или округления) могут возрасти при вычислении решения для больших х.

Пример

Дано уравнение

.

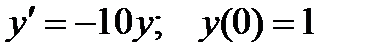Точное решение: y = e^-10x.

Все методы Рунге–Кутты второго порядка дадут приближенную формулу при вычислении решения для больших х следующего вида:

y_m+1 = (1 – 10h + 50h²)^m.

При h > 0,2 сумма, стоящая в скобках, становится больше 1.

Следовательно, при возрастании m y неограниченно возрастает. С другой стороны, точное решение убывает, стремясь к нулю.

Это явление называется частичной неустойчивостью по Майерсу. Ее характерная особенность – зависимость от h.

6.3 Обыкновенные ДУ. Методы прогноза и коррекции

B методах Рунге–Кутты при вычислении следующей точки x_m+1, y_m+1 используется информация только о точке х_m , у_m, но не о предыдущих.

В методах второго порядка и выше приходится вычислять значение функции в одной или в нескольких промежуточных точках. Это представляется нерациональным: если процесс интегрирования продвинулся на несколько шагов, у нас есть дополнительная информация – информация о предыдущих точках решения.

В методах Рунге–Кутты информация о предыдущих точках решения не используется, а также отсутствуют достаточно простые способы оценки ошибки.

Поэтому были развиты другие методы решения дифференциальных уравнений – методы прогноза и коррекции.

Особенность этих методов – с их помощью нельзя начать решение уравнения, т. к. в них не только возможно, но и необходимо использовать информацию о предыдущих точках решения.

Из названия ясна идея метода – делается «предсказание» значения y_m+1, а затем используется тот или иной метод для «корректировки» этого значения. Корректировка может производиться неоднократно.

Для прогноза используется формула второго порядка

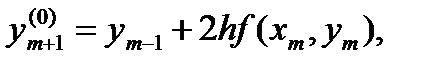(6.24)

где верхний индекс (0) означает исходное приближение к y_m+1, т. е. предсказанное значение.

Из формулы (6.24) следует, что с ее помощью нельзя вычислить у₁ – для вычисления у₁ потребовалась бы точка, расположенная перед начальной точкой у₀.

Методы прогноза и коррекции (в отличие от методов Рунге–Кутты) не являются самостартующими.

Чтобы начать решение, часто используется метод Рунге–Кутты. Теперь требуется некоторый метод коррекции предсказанного значения. Этапы поиска решения показаны на рис. 6.5 и 6.6. Поскольку нам приближенно известна величина y_m+1, то можно вычислить наклон касательной в точке x_m+1, y⁽⁰⁾_m+1. Эта касательная изображена на рис. 6.6 и обозначена L₂.

Прямая L₁ на рис. 6.5 представляет собой то же самое, что и на рис. 6.4, и тангенс угла ее наклона равен f (x_m, у_m).

Рис. 6.5. Геометрическое представление прогнозирующей формулы второго порядка

Рис. 6.6. Геометрическое представление формулы коррекции второго порядка

Точка пересечения линии L с ординатой х = x_m+1 дает новое приближение к y_m+1.

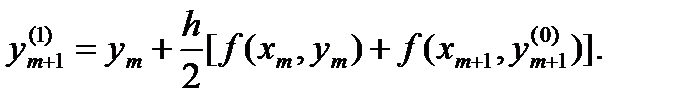
Назовем это приближение скорректированным значением y⁽¹⁾_m+1. Вычислить его можно по формуле

Можно попытаться найти новое, по-видимому, еще лучшее приближение к y_m+1, используя значение y⁽¹⁾_m+1 и корректируя снова.

В общем случае, i-е приближение к y_m+1 вычисляется по формуле

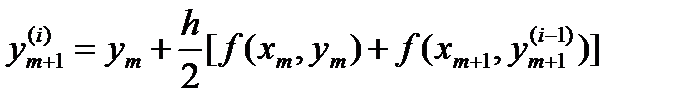(6.25)

для i = 1, 2, 3, … .

Итерационный процесс прекращается, когда

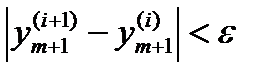(6.26)

для некоторого положительного ε.

Возникает естественный вопрос, удастся ли вообще когда-нибудь удовлетворить условию (6.26), т. е. сходится ли процесс вообще?

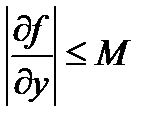
Можно показать, что если производная 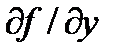ограничена, т. е. можно найти такое М, что

то при выполнении условия для h

,

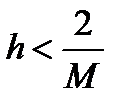(6.27)

разница между последовательными скорректированными значениями стремится к нулю и процесс сходится.

Нужно четко представлять себе, что же именно было показано.

Мы показали, что последовательные значения y⁽ⁱ⁾_m+1 сходятся к некоторому определенному значению, но вовсе не обязательно к точному решению уравнения.

Разница между тем и другим представляет собой ошибку ограничения, которую мы рассмотрим позже.

Также мы рассмотрим вопрос о скорости сходимости итерационного процесса. Очевидно, что чем меньше h, тем скорее процесс будет сходиться.

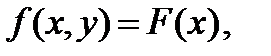
Рассмотрим внимательнее формулу коррекции (6.25). Предположим, что f является функцией только от х, т. е.

так что

.

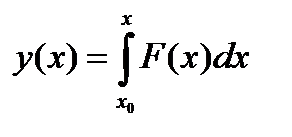(6.28)

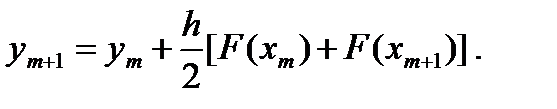
Тогда

Здесь опущены верхние индексы при y_m+1, т. к. первое же значение y_m+1 будет «точным» (если пренебречь ошибками ограничения и округления).

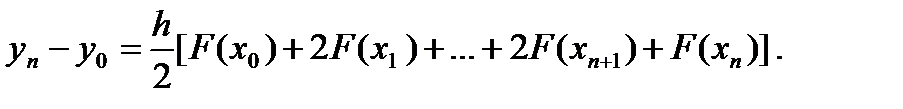
Из этой формулы легко получить

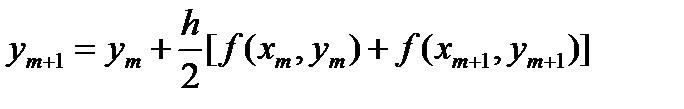
Это просто формула трапеций для вычисления интеграла (6.28), где x = x₀ + nh. Таким образом, рассмотренная нами формула коррекции является обобщением формулы трапеций, так же как классический метод Рунге–Кутты оказался обобщением формулы Симпсона.

Заметим, что формула коррекции

является неявной в том смысле, что y_m+1 входит и в правую, и в левую ее части, причем слева стоит то значение, которое должно быть вычислено в качестве следующего приближения, а справа стоит предыдущее приближение.