Чувак, тебе пиздец как не повезло j

Рассмотрим вывод расчетных формул для касательных напря­жений. Выделим из бруса, испытывающего поперечный изгиб, элемент длиной dz (рис. а).

Продольным горизонтальным сечением, проведенным на расстоянии y от нейтральной оси, разделим элемент на две части (рис. в) и рассмотрим равновесие верхней части, имеющей основание шириной b. При этом с учетом закона парности касательных напряжений, получим, что касательные напряжения в поперечном сечении равны касательным напряжениям, возникающим в продольных сечениях (рис. б). С учетом данного обстоятельства и из допущения о том, что касательные напряжения по площади b×dz распределены равномерно, используя условие åz = 0, получим:

N^* - N^* - dN^* + t× b×dz = 0,

откуда

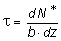. (1)

где N^* - равнодействующая нормальных сил s×dF в левом попереч­ном сечении элемента dz в пределах заштрихованной площади F^* (рис. г):

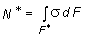. (2)

С учетом 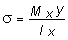последнее выражение можно представить в виде

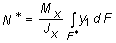, (3)

где 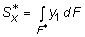- статический момент части поперечного сечения, расположенной выше координаты y (на рис. б эта область за­штрихована). Следовательно, (3) можно переписать в виде

,

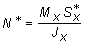откуда

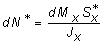. (4)

В результате совместного рассмотрения (1) и (4) получим

,

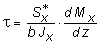или окончательно

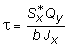. (5)

Полученная формула (5) носит имя русского ученого Д.И. Журавского.

45. Главные напряжения при изгибе.

Я НЕ ЗНАЮ, ЧТО ТУТ НАПИСАЛ, НО В ИНТЕРНЕТЕ ТОЛЬКО ТАК СОКРАТИЛ

ЕСЛИ ЧТО, ПОГУГЛИ САМОСТОЯТЕЛЬНО J

.

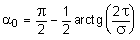Согласно этому выражению, экстремальные напряжения возникают на двух взаимно перпендикулярных площадках, называемых главными, а сами напряжения - главными напряжениями.

Сопоставляя выражения t_a и 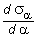, имеем:

,

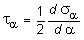откуда и следует, что касательные напряжения на главных пло­щадках всегда равны нулю.

В заключение, с учетом известных тригонометрических тож­деств:

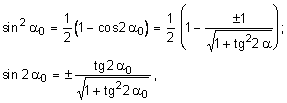
и формулы ,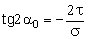

определим главные напряжения, выражая из через s и t:

.

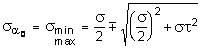Полученное выражение имеет важное значение в теории проч­ности изгибаемых элементов, позволяющее производить расчеты их прочности, с учетом сложного напряженного состояния, присущее поперечному изгибу.

46. Условия прочности по нормальным напряжениям при изгибе.

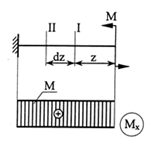
Рис. 6.2

Из балки, нагруженной только изгибающим моментом рис. (6.2) вырежем фрагмент длинной dz, (рис. 6.3)

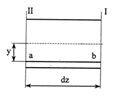
Рис. 6.3

При изгибе кривизна оси балки:

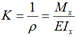
относительное удлинение слоя ab (рис. 6.4).

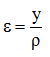
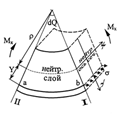
Рис. 6.4

Распределение нормальных напряжений: по ширине сечения равномерное (const), по высоте сечения

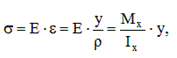
максимальные нормальные напряжения в наиболее удаленных от нейтральной оси точках сечения.

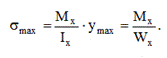
Условие прочности при изгибе балок по нормальным напряжениям:

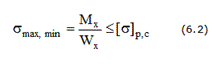
47. Основные типы задач при расчете на прочность при поперечном изгибе.

48. Устойчивость продольной формы сжатых стержней в упругой стадии.

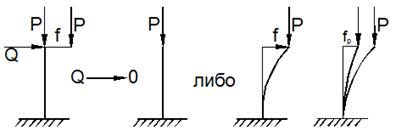
Под устойчивостьюпонимают способность систем сохранять их состояние равновесия или движения во времени под действием малых возмущений. Под неустойчивостью понимают способность систем при действии весьма малых возмущений получать большие перемещения.

равновесие упругой системы при заданных внешних силах считается устойчивым в смысле Эйлера, если после статического приложения и последующего снятия малой возмущающей силы система возвращается к своему исходному состоянию (рис. 9.3). В противном случае исходное состояние равновесия системы считается неустойчивым.

49. Формула Эйлера для критической силы.

Запишем дифф. уравнение изогнутой оси балки

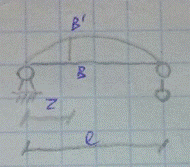
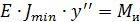
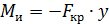
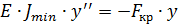
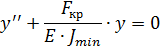
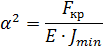
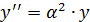
Решение ищем в виде:

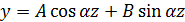
Запишем граничные условия

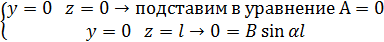
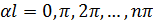
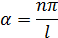
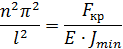
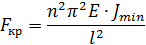
Формула Эйлера

50. Границы применимости формулы Эйлера при продольном изгибе.

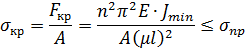
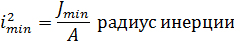
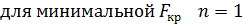
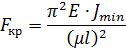
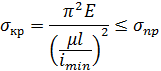
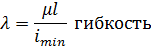
51. Формула Ясинского при напряжениях, превышающих предел пропорциональности.

В ситуациях, когда напряжения превышают предел пропорциональности, получение теоретического решения осложняется, т.к. зависимость между напряжениями и деформациями становится нелинейной. В связи с этим, в этих случаях пользуются эмпирическими зависимостями. В частности, Ф.С. Ясинский предложил следующую формулу для критических по устойчивости напряжений:

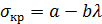
где a, b - постоянные, зависящие от материала.

52. Практический метод расчета сжатых стержней на устойчивость.

В основу расчетов сжатых стержней на устойчивость положено требование, согласно которому допустимое напряжение должно быть меньше не только предела текучести .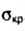

Разделив предел текучести при сжатии 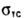на коэффициент запаса по текучести n_т получим допустимое напряжение на сжатие для коротких стержней (типа образцов):

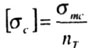
Теперь это допустимое напряжение надо еще уменьшить, чтобы оно было меньше 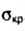. Но критическое напряжение 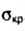зависит от гибкости стержня 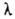(чем больше 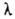, тем меньше 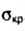) и от материала стойки. Эти факторы учтены в 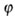-коэффициенте понижения допускаемых напряжений. Коэффициент 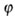берется из таблиц в зависимости от 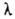и материала.

Допускаемая сжимающая сила для гибкого стержня определяется по формуле

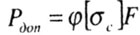
где 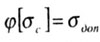- допустимое сжимающее напряжение с учетом устойчивости.

Различают прямую и обратную задачу проектировочного расчета

53. Рациональные формы сечений сжатых стержней.

При заданных нагрузке, длине стержня, допускаемом напряжении форма и размеры поперечного сечения сжатого стержня характеризуются радиусом инерции. Радиус инерции величина размерная. 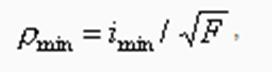Для сравнения различных сечений между собой более удобной является безразмерная величина, которую называют удельным радиусом инерции

Значение удельного радиуса инерции бывает разным для разных фигур, от 0,204 у прямоугольника до 1,53 у кольца.

Наименее выгодными являются прямоугольные сплошные сечения, у которых моменты инерции относительно главных осей не равны между собой и, следовательно, не соблюдается принцип равной устойчивости стержня в обеих главных плоскостях инерции.

Наиболее выгодными являются кольцевые, а также коробчатые тонкостенные сечения. Подсчеты показывают, что замена сжатых сечений в виде уголков и двутавров трубчатыми стержнями дает экономию в материале до 20-40%.</