Не уверен, правильно это или нет

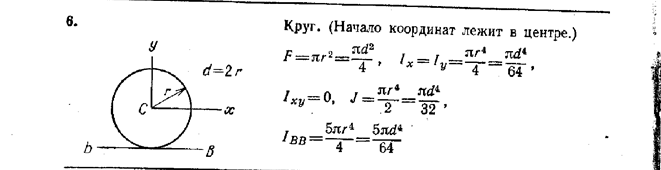
29. Одноосное (центральное) растяжение и сжатие.

Растяжение-сжатие — вид продольной деформации стержня или бруса, возникающий в том случае, если нагрузка к нему прикладывается по его продольной оси. Вызывается как силами, приложенными к концам стержня, так и силами, распределёнными по объёму (силы инерции и тяготения).

Растяжение вызывает удлинение стержня (также возможен разрыв и остаточная деформация), сжатие вызывает укорочение стержня (возможна потеря устойчивости и возникновение продольного изгиба).

В поперечных сечениях бруса возникает один внутренний силовой фактор — нормальная сила. Если растягивающая или сжимающая сила параллельна продольной оси бруса, но не проходит через неё, то стержень испытывает т. н. внецентренное растяжение (сжатие). В этом случае за счёт эксцентриситета приложения нагрузки в стержне кроме растягивающих (сжимающих) напряжений возникают ещё и изгибные напряжения.

Напряжение вдоль оси прямо пропорционально растягивающей или сжимающей силе и обратно пропорционально площади поперечного сечения.

30. Построение эпюр продольных сил и нормальных напряжений при растяжении и сжатии

Построенные эпюры внутренних продольных сил для стержня при его растяжении-сжатии легко можно проверить по скачкам.

В сечениях стержня, где приложена внешняя продольная сила, на эпюре должен быть скачок значения N на величину соответствующей силы

Если при одинаковой площади внутренние силы различаются на разных силовых участках. то на этих участках и нормальные напряжения тоже будут отличаться.

Знак напряжений зависит от знака соответствующей внутренней продольной силы.
Значения внутренних сил принимаются с построенной ранее эпюры N.

31. Напряжения в поперечных сечениях стержня при растяжении и сжатии

Два любых поперечных сечения при растяжении бруса остаются плоскими и параллельными между собой, но удаляются друг от друга на некоторую величину; на такую же величину удлиняется каждое волокно. А так как одинаковым удлинениям соответствуют одинаковые напряжения, то и напряжения в поперечных сечениях всех волокон (а следовательно, и во всех точках поперечного сечения бруса) равны между собой.

Это позволяет в выражении вынести величину сигма за знак интеграла. Таким образом,

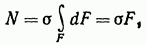
откуда

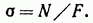
Итак, в поперечных сечениях бруса при центральном, растяжении или сжатии возникают равномерно распределенные нормальные напряжения, равные отношению продольной силы к площади поперечного сечения.

32. Закон Гука при растяжении и сжатии

Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука. Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению. Закон Гука в виде равенства: σ = Еε.

Коэффициент пропорциональности Е характеризует жесткость материала, т. е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода.

Модуль упругости и напряжение выражаются в одинаковых единицах:

[Е] = [σ]/[ε] = Па.

Если в формулу закона Гука подставим выражения

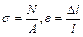
то получим:Δl = Nl/(EA).

Произведение ЕА, стоящее в знаменателе, называется жесткостью сечения при растяжении и сжатии; оно характеризует одновременно физико-механические свойства ма­териала и геометрические размеры поперечного сечения бруса.

Эта формула читается так: абсолютное удлинение или укорочение прямо пропорционально продольной силе, длине и обратно пропорционально жесткости сечения бруса. При прочих равных условиях, чем жестче материал, тем меньше он деформируется:

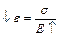
33. Коэффициент Пуассона, модуль Юнга.

Для малых упругих деформаций натяжение 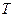(давление 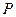) пропорционально относительному удлинению (относительному сжатию) — ( ),

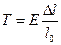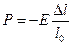где 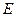– модуль Юнга (постоянная, зависящая только от материала стержня и его физического состояния).

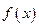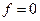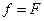Модуль Юнга – натяжение, которое необходимо приложить к стержню, чтобы его длина увеличилась в два раза. Вычислим упругую энергию растянутого стержня. Приложим к стержню растягивающую силу и будем постепенно (непрерывно и медленно) увеличивать ее от до . Удлинение будет меняться от 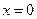до 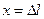. По закону Гука ,

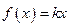где 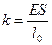– коэффициент упругости.

Под действием растягивающей или сжимающей силы 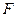изменяются не только продольные, но и поперечные размеры стержня. Если сила ­ растягивающая, то поперечные размеры стержня уменьшаются. Если она сжимающая, то они увеличиваются. 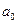– толщина стержня до деформации (диаметр, если стержень круглый, одна из сторон, если прямоугольный). 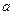– толщина стержня после деформации. Если растягиваем стержень, то 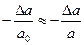– относительное поперечное сжатие ( ).

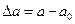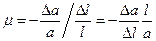– коэффициент Пуассона.

34. Основные типы задач при расчете на прочность растянутых (сжатых) стержней.

35. Сдвиг. Основные понятия.

Сдвиг- это вид деформации, при котором одна часть стержня смещается относительно другой. Деформация сдвига будет происходить, если к стержню приложить две равные по модулю противоположно направленные силы (P), перпендикулярные к его оси z. Расстояние между этими силами ( 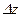) должно быть малым, чтобы можно было пренебречь моментом, создаваемым этими силами.

Применив метод сечений (разрезав стержень между силами P), можно легко установить, что в поперечном сечении стержня возникает только одно внутреннее усилие – поперечная сила .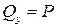

Деформация сдвига возникает и при кручении стержня.

36. Напряженное состояние и деформации при чистом сдвиге

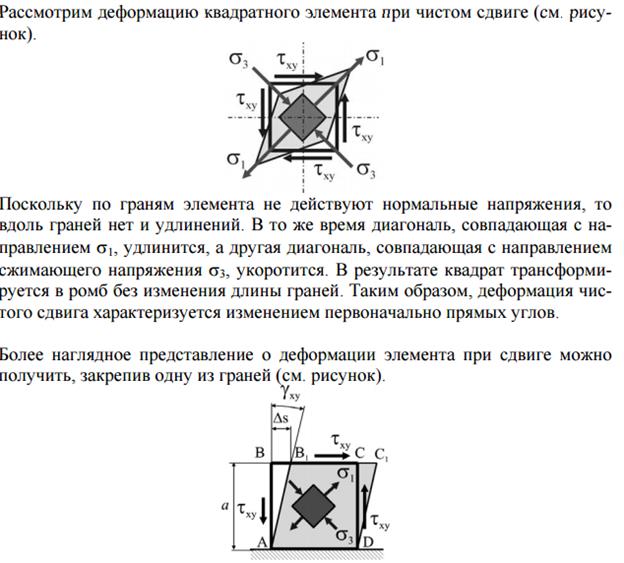
37. Изгиб, основные понятия.

38. Поперечные силы и изгибающие моменты.

Внутренние силовые факторы в сечениях балок — поперечная сила Q и изгибающий момент М — зависят от внешней нагрузки и изменяются по длине балки. Законы их изменения представляются некоторым уравнениями, где аргументами являются координаты z поперечных сечений балки, а функциями — Q или М. Эти уравнения удобно представлять в виде эпюр, ординаты которых для любых значений абсциссы z дают соответствующие значения изгибающего момента М или поперечной силы Q. Эпюры изгибающих моментов и поперечных сил строятся аналогично эпюрам продольных сил и крутящих моментов.

39. Дифференциальные зависимости между М и Q.

Дифференциальные зависимости между распределенной нагрузкой, поперечной силой и изгибающим моментом:

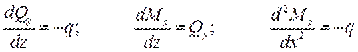
Дифференциальные зависимости используются для контроля правильности построенных эпюр поперечных сил 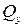и изгибающих моментов.

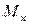Помимо дифференциальных зависимостей существуют интегральные зависимости, получаемые из формул дифференциальных зависимостей. Например, изгибающий момент равен определенному интегралу по длине участка балки. Используя интегральную зависимость между изгибающим моментом и поперечной силой и аналитическое выражение поперечных сил, можно построить эпюру изгибающих моментов, не определяя выражение для них.

В формулах дифференциальных и интегральных зависимостей распределенная нагрузка (q) положительна, если направлена вниз.

40. Правило знаков для изгибающих моментов и поперечных сил.

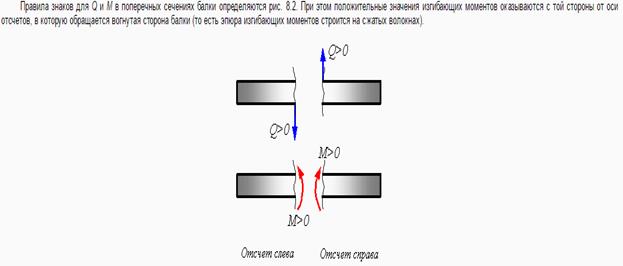
41. Построение эпюр поперечных сил и изгибающих моментов.

Для определения сечений, в которых появляются наибольшие напряжения, необходимо знать изменения моментов и поперечных сил по длине всей балки. Обычно для большей наглядности изменения Q и M представляют графически в виде эпюр - графиков изменения Q и M.

Построение эпюр Q и M часто начинают с определения опорных реакций. Далее балку разбивают на отдельные участки, например, между сосредоточенными силами. На каждом участке намечают произвольное сечение на расстоянии от начала координат (или от какого-либо конца балки) и находят аналитические выражения для Q и M, исходя из данных для них определений (Q - алгебраическая сумма сил, приложенных к отсеченной части, M - сумма моментов внешних сил, приложенных к отсеченной части). По ним строят соответствующие графики.

При построении эпюр положительные Q и M откладывают вверх от оси, а отрицательные - вниз. Для эпюры М говорят еще иногда, что ее строят на сжатых волокнах.

В строительстве положительную Q откладывают вверх от оси, а положительный M- вниз, т.е. на растянутых волокнах.

42. Контроль построения эпюр поперечных сил и изгибающих моментов.

1. В сечениях, где приложены сосредоточенные силы, на эпюрах продольной и поперечной сил происходит скачек на величину этих сил в направлении их действия, а эпюра изгибающего момента претерпевает излом в сторону действия сосредоточенных сил.

2. На участках стержней, где отсутствует равномерно распределенная нагрузка, продольная и поперечная сила величины постоянные, а эпюра изгибающего момента изменяется по закону наклонной прямой.

3. На участках, где приложена равномерно распределенная нагрузка, эпюры продольной и поперечной сил изменяются по закону наклонной прямой на величину равнодействующей распределенной нагрузки. При положительном значении распределенной нагрузки эпюры возрастают, при отрицательном – убывают.

4. В сечениях на свободном или шарнирно опертом концах балки, где отсутствует сосредоточенный изгибающий момент, изгибающий момент равен нулю.

5. На участках, где приложена поперечная равномерно распределенная нагрузка, эпюра изгибающего момента изменяется по закону квадратной параболы, выпуклостью навстречу направлению действия распределенной нагрузки.

6. В сечениях, где приложен сосредоточенный изгибающий момент, на эпюре изгибающего момента происходит скачек на его величину в направлении его действия.

7. В сечении, где поперечная сила равна нулю, изгибающий момент имеет экстремальное значение.

8. На участках, где поперечная сила равна нулю, изгибающий момент величина постоянная.

9. На участках, где поперечная сила положительна, эпюра изгибающего момента возрастает, где отрицательна – убывает.

10. Изгибающий момент в любом сечении равен площади эпюры поперечной силы левой или правой отсеченной части балки плюс приложенные к ним сосредоточенные изгибающие моменты.

43. Чистый изгиб, нормальные напряжения.

При выводе формулы для вычисления нормальных напряжений рассмотрим такой случай изгиба, когда внутренние силы в сечениях балки приводятся только к изгибающему моменту, а поперечная сила оказывается равной нулю. Этот случай изгиба носит названиечистого изгиба. Рассмотрим средний участок балки, подвергающийся чистому изгибу.

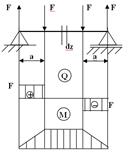В нагруженном состоянии балка прогибается так,что ее нижние 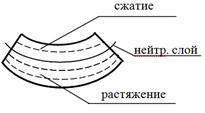волокна удлиняются,а верхние укорачиваются.

Поскольку часть волокон балки растягивается, а часть сжимается, причем переход от растяжения к сжатию происходит плавно, без скачков, в средней части балки находится слой, волокна которого только искривляются, но не испытывают ни растяжения, ни сжатия. Такой слой называют нейтральным слоем. Линия, по которой нейтральный слой пересекается с поперечным сечением балки, называетсянейтральной линией или нейтральной осью сечения. Нейтральные линии нанизаны на ось балки.Нейтральная линия — это линия, в которой нормальные напряжения равны нулю.

Линии, проведенные на боковой поверхности балки перпендикулярно оси, остаются плоскими при изгибе. Эти опытные данные позволяют положить в основу выводов формулгипотезу плоских сечений (гипотеза Бернулли). Согласно этой гипотезе сечения балки плоские и перпендикулярные к ее оси до изгиба, остаются плоскими и оказываются перпендикулярными изогнутой оси балки при ее изгибе.

44. Касательные напряжения, формула Д.И.Журавского.