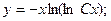Подставляем полученное соотношение в исходное уравнение
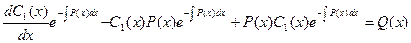
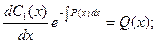
Из этого уравнения определим переменную функцию С1(х):
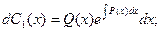
Интегрируя, получаем:
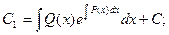
Подставляя это значение в исходное уравнение, получаем:

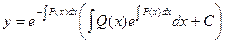 .
.
Таким образом, мы получили результат, полностью совпадающий с результатом расчета по методу Бернулли.
При выборе метода решения линейных дифференциальных уравнений следует руководствоваться простотой интегрирования функций, входящих в исходный интеграл.
Далее рассмотрим примеры решения различных дифференциальных уравнений различными методами и сравним результаты.
Пример. Решить уравнение 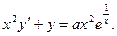
Сначала приведем данное уравнение к стандартному виду: 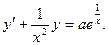
Применим полученную выше формулу: 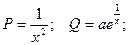
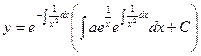
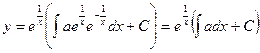
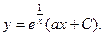
Уравнение Бернулли.
Определение. Уравнением Бернуллиназывается уравнение вида
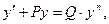
где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.
Для решения уравнения Бернулли применяют подстановку 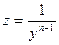 , с помощью которой, уравнение Бернулли приводится к линейному.
, с помощью которой, уравнение Бернулли приводится к линейному.
Для этого разделим исходное уравнение на yn.
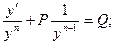
Применим подстановку, учтя, что 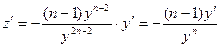 .
.
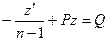
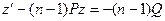
Т.е. получилось линейное уравнение относительно неизвестной функции z.
Решение этого уравнения будем искать в виде:

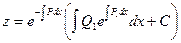

Пример. Решить уравнение 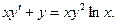
Разделим уравнение на xy2: 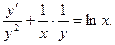
Полагаем 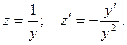
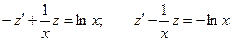 .
.
Полагаем 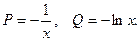
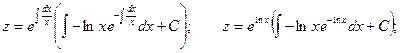
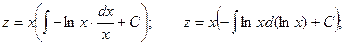
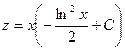
Произведя обратную подстановку, получаем:
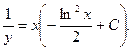
Пример. Решить уравнение 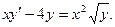
Разделим обе части уравнения на 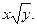
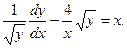
Полагаем 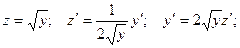
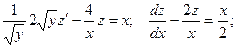
Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:
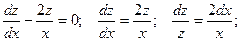
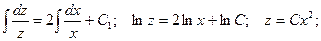
Полагаем C = C(x) и подставляем полученный результат в линейное неоднородное уравнение, с учетом того, что:
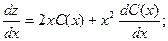
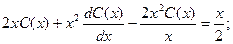
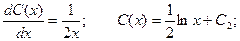
Получаем: 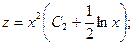
Применяя обратную подстановку, получаем окончательный ответ:
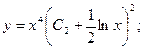
Уравнения в полных дифференциалах (тотальные).
Определение. Дифференциальное уравнение первого порядка вида:
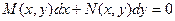
называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции 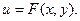
Интегрирование такого уравнения сводится к нахождению функции u, после чего решение легко находится в виде: 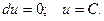
Таким образом, для решения надо определить:
1) в каком случае левая часть уравнения представляет собой полный дифференциал функции u;
2) как найти эту функцию.
Если дифференциальная форма 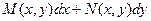 является полным дифференциалом некоторой функции u, то можно записать:
является полным дифференциалом некоторой функции u, то можно записать:
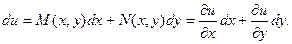
Т.е. 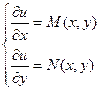 .
.
Найдем смешанные производные второго порядка, продифференцировав первое уравнение по у, а второе – по х:
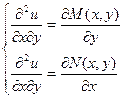
Приравнивая левые части уравнений, получаем необходимое и достаточное условие того, что левая часть дифференциального уравнения является полным дифференциалом. Это условие также называется условием тотальности.

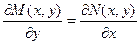
Теперь рассмотрим вопрос о нахождении собственно функции u.
Проинтегрируем равенство 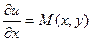 :
:
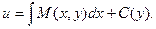
Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию С(у), т.к. при интегрировании переменная у полагается постоянным параметром.
Определим функцию С(у).
Продифференцируем полученное равенство по у.
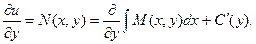
Откуда получаем: 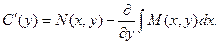
Для нахождения функции С(у) необходимо проинтегрировать приведенное выше равенство. Однако, перед интегрированием надо доказать, что функция С(у) не зависит от х. Это условие будет выполнено, если производная этой функции по х равна нулю.
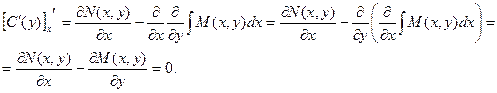
Теперь определяем функцию С(у):
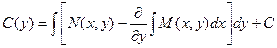
Подставляя этот результат в выражение для функции u, получаем:
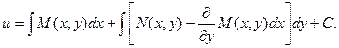
Тогда общий интеграл исходного дифференциального уравнения будет иметь вид:

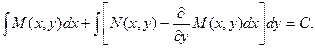
Следует отметить, что при решении уравнений в полных дифференциалах не обязательно использовать полученную формулу. Решение может получиться более компактным, если просто следовать методу, которым формула была получена.
Пример. Решить уравнение 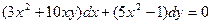
Проверим условие тотальности: 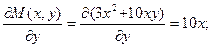
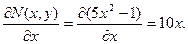
Условие тотальности выполняется, следовательно, исходное дифференциальное уравнение является уравнением в полных дифференциалах.
Определим функцию u.
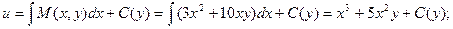
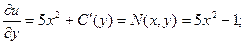
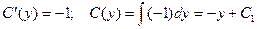 ;
;
Итого, 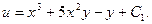
Находим общий интеграл исходного дифференциального уравнения:
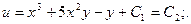
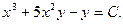
Уравнения вида y = f(y’) иx = f(y’).
Решение уравнений, не содержащих в одном случае аргумента х, а в другом – функции у, ищем в параметрической форме, принимая за параметр производную неизвестной функции.
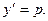
Для уравнения первого типа получаем: 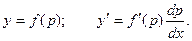
Делая замену, получаем: 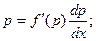
В результате этих преобразований имеем дифференциальное уравнение с разделяющимися переменными.
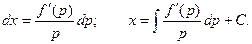
Общий интеграл в параметрической форме представляется системой уравнений:

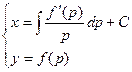
Исключив из этой системы параметр р, получим общий интеграл и не в параметрической форме.
Для дифференциального уравнения вида x = f(y’) с помощью той же самой подстановки и аналогичных рассуждений получаем результат:

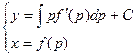
Уравнения Лагранжа и Клеро.
( Алекси Клод Клеро (1713 – 1765) французский математик
ин. поч. член Петерб. АН )
Определение. Уравнением Лагранжаназывается дифференциальное уравнение, линейное относительно х и у, коэффициенты которого являются функциями от y’.
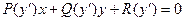
Для нахождения общего решение применяется подстановка p = y’.
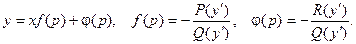
Дифференцируя это уравнение,c учетом того, что 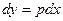 , получаем:
, получаем:
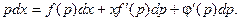
Если решение этого (линейного относительно х) уравнения есть 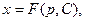 то общее решение уравнения Лагранжа может быть записано в виде:
то общее решение уравнения Лагранжа может быть записано в виде:

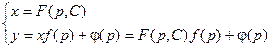
Определение. Уравнением Клероназывается уравнение первой степени (т.е. линейное) относительно функции и аргумента вида:
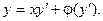
Вообще говоря, уравнение Клеро является частным случаем уравнения Лагранжа.
С учетом замены 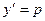 , уравнение принимает вид:
, уравнение принимает вид:
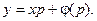
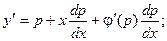
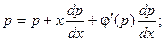
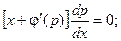
Это уравнение имеет два возможных решения:
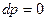 или
или 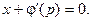
 В первом случае:
В первом случае: 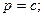
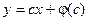
Видно, что общий интеграл уравнения Клеро представляет собой семейство прямых линий.
Во втором случае решение в параметрической форме выражается системой уравнений:
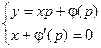
Исключая параметр р, получаем второе решение F(x, y) = 0. Это решение не содержит произвольной постоянной и не получено из общего решения, следовательно, не является частным решением.
Это решение будет являться особым интегралом. ( См. Особое решение. )
Далее рассмотрим примеры решения различных типов дифференциальных уравнений первого порядка.
Пример. Решить уравнение с заданными начальными условиями.
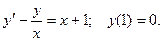
Это линейное неоднородное дифференциальное уравнение первого порядка.
Решим соответствующее ему однородное уравнение.
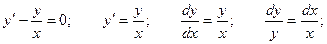
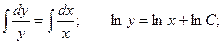
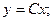
Для неоднородного уравнения общее решение имеет вид:
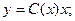
Дифференцируя, получаем: 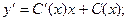
Для нахождения функции С(х) подставляем полученное значение в исходное дифференциальное уравнение:
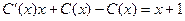
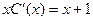
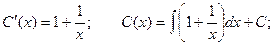
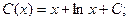
 Итого, общее решение:
Итого, общее решение: 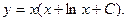
C учетом начального условия 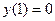 определяем постоянный коэффициент C.
определяем постоянный коэффициент C.
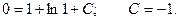

Окончательно получаем: 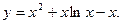
Для проверки подставим полученный результат в исходное дифференциальное уравнение: 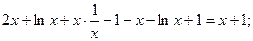 верно
верно
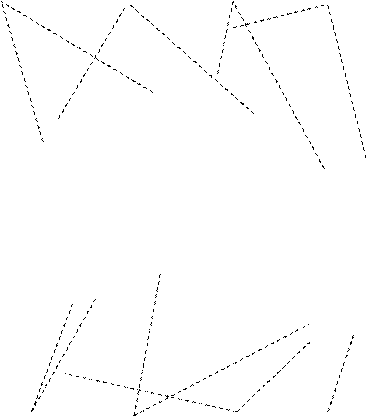
Ниже показан график интегральной кривой уравнения.
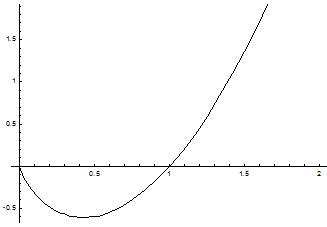
Пример. Найти общий интеграл уравнения 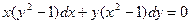 .
.
Это уравнение с разделяющимися переменными.
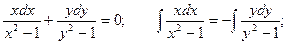
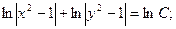

Общий интеграл имеет вид: 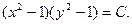
Построим интегральные кривые дифференциального уравнения при различных значениях С.
С = - 0,5 С = -0,02 С = -1 С = -2
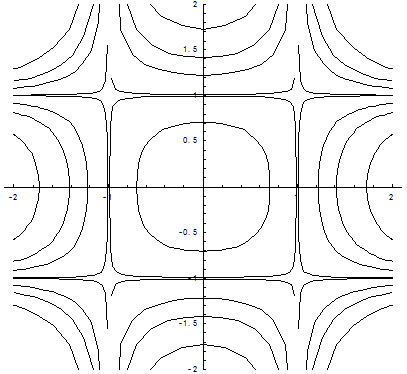
С = 0,02 С = 0,5 С = 1 С = 2
Пример. Найти решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
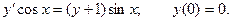
Это уравнение с разделяющимися переменными.
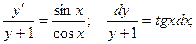
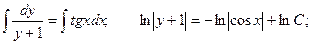
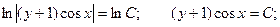
 Общее решение имеет вид:
Общее решение имеет вид: 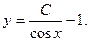
Найдем частное решение при заданном начальном условии у(0) = 0.
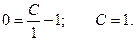
 Окончательно получаем:
Окончательно получаем: 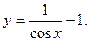
Пример. Решить предыдущий пример другим способом.
Действительно, уравнение 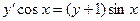 может быть рассмотрено как линейное неоднородное дифференциальное уравнение.
может быть рассмотрено как линейное неоднородное дифференциальное уравнение.
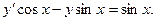
Решим соответствующее ему линейное однородное уравнение.
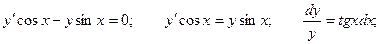
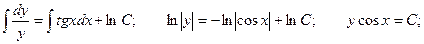
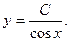
Решение неоднородного уравнения будет иметь вид: 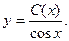
Тогда 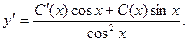
Подставляя в исходное уравнение, получаем:
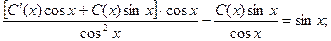
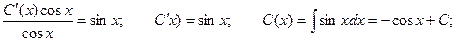

Итого 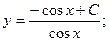
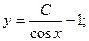

С учетом начального условия у(0) = 0 получаем 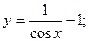
Как видно результаты, полученные при решении данного дифференциального уравнения различными способами, совпадают.
При решении дифференциальных уравнений бывает возможно выбирать метод решения, исходя из сложности преобразований.
Пример. Решить уравнение 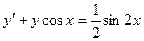 с начальным условием у(0) = 0.
с начальным условием у(0) = 0.
Это линейное неоднородное уравнение. Решим соответствующее ему однородное уравнение.
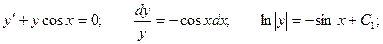
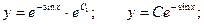
Для линейного неоднородного уравнения общее решение будет иметь вид:
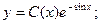
Для определения функции С(х) найдем производную функции у и подставим ее в исходное дифференциальное уравнение.
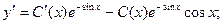
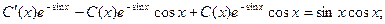

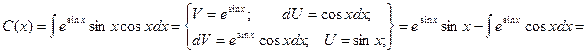
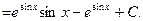

Итого 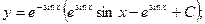
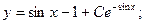
Проверим полученное общее решение подстановкой в исходное дифференциальное уравнение.
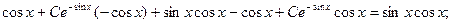 (верно)
(верно)
Найдем частное решение при у(0) = 0.
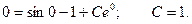

Окончательно 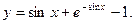
Пример. Найти решение дифференциального уравнения
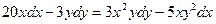
с начальным условием у(1) = 1.
Это уравнение может быть преобразовано и представлено как уравнение с разделенными переменными.
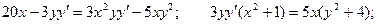
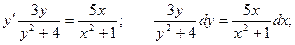
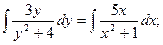
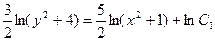
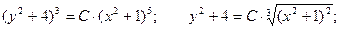
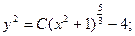

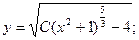
С учетом начального условия:
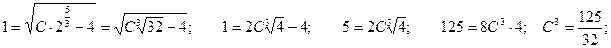
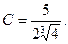

Окончательно 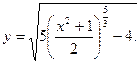
Пример. Решить дифференциальное уравнение 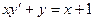 с начальным условием у(1) = 0.
с начальным условием у(1) = 0.
Это линейное неоднородное уравнение.
Решим соответствующее ему однородное уравнение.
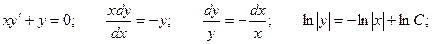
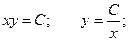
Решение неоднородного уравнения будет иметь вид:
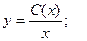
Подставим в исходное уравнение:
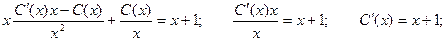
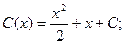

Общее решение будет иметь вид: 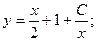
 C учетом начального условия у(1) = 0:
C учетом начального условия у(1) = 0: 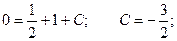
Частное решение: 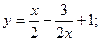
Пример. Найти решение дифференциального уравнения 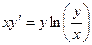 с начальным условием у(1) = е.
с начальным условием у(1) = е.
Это уравнение может быть приведено к виду уравнения с разделяющимися переменными с помощью замены переменных.
Обозначим: 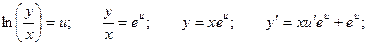
Уравнение принимает вид:
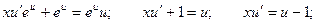
Получили уравнение с разделяющимися переменными.
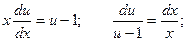
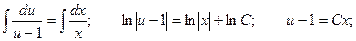
Сделаем обратную замену: 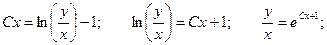

Общее решение: 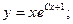
C учетом начального условия у(1) = е: 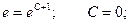
 Частное решение:
Частное решение: 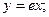
Второй способ решения.
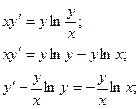
Получили линейное неоднородное дифференциальное уравнение. Соответствующее однородное:
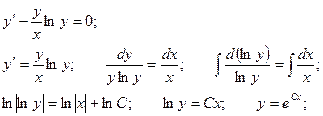
Решение исходного уравнения ищем в виде: 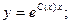
Тогда 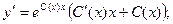
Подставим полученные результаты в исходное уравнение:
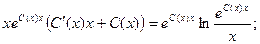
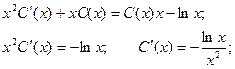
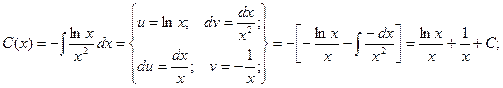
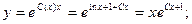

Получаем общее решение: 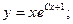
Пример. Решить дифференциальное уравнение 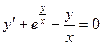 с начальным условием у(1)=0.
с начальным условием у(1)=0.
В этом уравнении также удобно применить замену переменных.
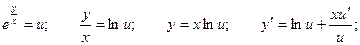
Уравнение принимает вид: 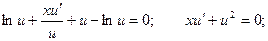
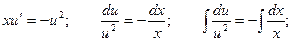
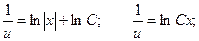
Делаем обратную подстановку: 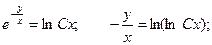

Общее решение: 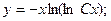
C учетом начального условия у(1) = 0: 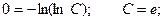

Частное решение: 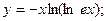
Второй способ решения.
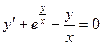
Замена переменной: 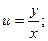
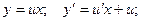
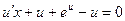
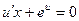
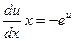
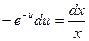
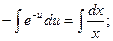
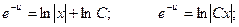


Общее решение: