Элементы алгебры логики высказываний.
Литература [1], часть 1, §§1-6; [2], глава 2, §2.1
Высказыванием называется предложение, к которому возможно применить понятия “истинно” или “ложно”. В математической логике не рассматривается сам смысл высказываний, а определяется только его истинность или ложность, что принято обозначать соответственно И или Л.
Основные логические операции над высказываниями:
1) отрицанием высказывания Р называется высказывание Р, которое истинно только тогда, когда высказывание Р ложно;
| P | P |
| И | Л |
| Л | И |
2) конъюнкцией двух высказываний P и Q называется высказывание P&Q,
истинное тогда и только тогда, когда истинны оба высказывания;
| P | Q | P&Q |
| И | И | И |
| Л | И | Л |
| И | Л | Л |
| Л | Л | Л |
3) дизъюнкцией двух высказываний P и Q называется высказывание PvQ,
ложное тогда и только тогда, когда оба высказывания ложны;
| P | Q | PvQ |
| И | И | И |
| Л | И | И |
| И | Л | И |
| Л | Л | Л |
4) импликацией двух высказываний P и Q называется высказывание P ⇒ Q ,
ложное тогда и только тогда, когда высказывание P истинно, а Q - ложно.
| P | Q | P ⇒ Q |
| И | И | И |
| Л | И | И |
| И | Л | Л |
| Л | Л | И |
5) эквиваленцией двух высказываний P и Q называется высказывание
P ⇔ Q , истинное тогда и только тогда, когда истинности высказываний совпадают.
| P | Q | P ⇔ Q |
| И | И | И |
| Л | И | Л |
| И | Л | Л |
| Л | Л | И |
Задачи 621 – 630
621)Даны два высказывания: Р - “Анна – студентка университета”, Q - “Анна играет в футбол”. На языке логики высказываний записать следующие утверждения:
1) “Анна не играет в футбол”;
2) “Анна – не студентка университета или Анна играет в футбол”;
3) “Анна – студентка университета и Анна не играет в футбол”;
4) “если Анна – студентка университета, то Анна не играет в футбол”.
622)Составить таблицу истинности для высказываний:
1) R1 = (P) ∨ Q;
2) R4= (P1⇒ P2) & Q.
623)Даны два высказывания: P – “Иван поет в хоре”, Q - “Иван любит химию”. На языке логики высказываний записать следующие утверждения:
1) “Иван не поет в хоре”;
2) “Иван не поет в хоре и Иван любит химию”;
3) “Иван не поет в хоре или Иван не любит химию”;
4) “если Иван любит химию, то Иван поет в хоре”.
624)Составить таблицу истинности для высказываний:
1) R1 = P ∨ (Q) ;
2) R2 = P & ((Q1 ) ⇔ Q2 );
625)Доказать эквивалентность высказываний:
R1 = X ⇒ Y и
R2 = (X ) ∨ Y .
626)Доказать истинность формулы
R = (X ) ⇒ ( X
⇒ Y )
627)Даны высказывания: X = “Джо умен”, Y = “Джим глуп”, Z = “Джо получит приз”. Для высказывания “Если Джо умен, а Джим глуп, то Джо получит приз” найти символическую форму и построить таблицу истинности.
628)Составить таблицу истинности для высказываний:
1) R1 = (P)&Q;
2) R2= (P1⇒ (P2)) ∨ Q.
629)Даны высказывания: X = ”Я сдам этот экзамен”, Y = “Я буду регулярно выполнять домашние задания”. Для высказывания “Я сдам этот экзамен
только в том случае, если буду регулярно выполнять домашние задания” найти символическую форму и построить таблицу истинности.
630)Доказать эквивалентность следующих высказываний:
 |
R1 = X ⇒ Y и R2 = X & Y
Элементы теории графов.
Литература [1], часть 5, §§ 1-5, 9,10; [2], глава 4, §§ 4.1,4.2
Графом называется непустое множество точек и множество отрезков, оба конца которых принадлежат этому множеству точек. Точки – это вершины графа, а отрезки, соединяющие вершины, - ребра графа. Обычно граф обозначается буквой Г, его вершины – заглавными буквами латинского алфавита, а ребра парой букв, которыми обозначены принадлежащие этим ребрам вершины. В некоторых случаях вершины и ребра не обозначаются.
Замечания:
1) В этом параграфе будут рассмотрены графы, в котором любые две вершины либо не соединены ребром, либо соединены однимребром. Такие графы называются простыми. Помимо простых графов существуют мультиграфы, в которых две вершины могут быть соединены несколькими ребрами (кратными ребрами), а также вершина может быть соединена сама с собой ребром, называемым петлей.
2) При изображении графов вершины обозначаются жирными точками, чтобы отличить их от точек пересечения ребер графа.
3) Существуют вершины графа, которые не принадлежат ни одному ребру графа. Такие вершины называются изолированными.
4) При изображении графа ребра могут быть прямолинейными или криволинейными отрезками произвольной длины. На рисунке изображен один и тот же граф, имеющий 4 вершины и 4 ребра.
Полным называется граф, у которого каждые две различные вершины соединены одним и только одним ребром. Каждая вершина полного графа принадлежит одному и
тому же числу ребер. Число ребер полного графа, который имеет n вершин,
вычисляется по формуле
2 n(n −1)
|
|
. Если граф не является полным, то его
можно преобразовать в полный граф, добавив недостающие ребра. Граф Г , с теми же вершинами, что и граф Г, и с теми и только теми ребрами, которые необходимо добавить к графу Г, чтобы из него получился полный граф, называется дополнением
графа Г.
Число ребер графа, которым принадлежит данная вершина, называется степенью этой вершины. Вершина называется четной, если ее степень четна, и нечетной, если ее степень нечетна. Степень любой вершины полного графа всегда на единицу меньше числа его вершин.
Теорема 1.Во всяком графе сумма степеней всех его вершин равна удвоенному числу ребер графа.
Теорема 2.Число нечетных вершин любого графа четно.
Теорема 3.Во всяком графе, число вершин которого не менее двух, всегда найдутся по меньшей мере две вершины с одинаковыми степенями.
Теорема 4.Если в графе с n вершинами (n > 2) только две вершины имеют одинаковую степень, то в этом графе всегда найдется или только одна вершина степени 0, или только одна вершина степени n – 1.
Путем в графе от вершины А1 (начало пути) до вершины Аm (конец пути) называется последовательность ребер графа, соединяющая вершину А1 с вершиной Аm, в которой каждые два соседних ребра имеют общую вершину и ни одно из ребер не встречаются более одного раза. Циклом в графе называется путь, в котором совпадают начало и конец пути. Путь (цикл) в графе называется простым, если он не проходит ни через одну вершину графа более одного раза. Длиной пути (цикла) называется число ребер этого пути (цикла).
Две вершины А и В данного графа называются связными (несвязными), если в графе существует (не существует) путь, начало и конец которого совпадают с этими вершинами. Граф называется связным (несвязным), если каждые (не каждые) две его вершины связные.
Путь, содержащий все ребра данного графа, называется эйлеровым путем этого графа. Цикл, содержащий все ребра данного графа, называется эйлеровым циклом этого графа. Граф, обладающий эйлеровым циклом, называется эйлеровым графом.
Теорема 5.Любой граф является эйлеровым графом, тогда и только тогда, когда он есть связный граф и имеет только четные вершины.
Гамильтоновым путем (циклом) называется путь (цикл), который проходит через каждую вершину графа только по одному разу. Гамильтонов путь (цикл) всегда является простым. Граф, обладающий гамильтоновым циклом, называется гамильтоновым графом.
Критерий существования гамильтонова графа еще не найден. Известно лишь несколько достаточных условий существования гамильтоновых циклов, среди которых следует выделить два. Во-первых, всякий полный граф является гамильтоновым. Во- вторых, если граф, кроме простого цикла, проходящего через все его вершины, содержит и другие ребра, то он также является гамильтоновым.
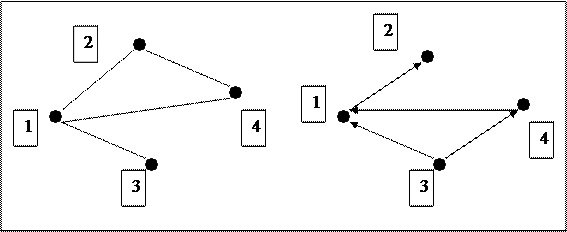
Ориентированным называется ребро графа, когда оно соединяет две вершины, одна из которых считается началом ребра, а другая – концом. На рисунке ориентированное ребро обозначается стрелкой, а в тексте ориентированное ребро с началом в вершине А и с концом в вершине В обозначается <АВ>.
Ориентированным графом называется граф, который имеет только ориентированные ребра. Одна и та же вершина ориентированного графа может служить началом для одних ребер и концом для других. Число выходящих из вершины А ориентированного графа ребер называется степенью выхода вершины А (обозначается степ.вых.А). Число входящих в вершину А ориентированного графа ребер называется степенью входа вершины А (обозначается степ.вх.А).
Теорема 6.В ориентированном графе с n вершинами А1, А2, …,Аn и p ребрами выполняются равенства:
1) степ.вх.А1 + степ.вх.А2 + …. + степ.вх.Аn =p;
2) степ.вых.А1 + степ.вых.А2 + …. + степ.выхАn=p.
Вершина ориентированного графа, у которой степень входа и степень выхода равны нулю, называется изолированной. Вершина ориентированного графа, у которой степень входа равна нулю, а степень выхода положительна, называется источником. Вершина ориентированного графа, у которой степень входа положительна, а степень выхода равна нулю, называется стоком.
Путем в ориентированном графе называется последовательность ориентированных ребер, такая, что конец любого предыдущего ребра совпадает с началом следующего и ни одно ребро не встречается более одного раза. Путь в ориентированном графе называется простым, если он не проходит ни через одну вершину более одного раза. Ориентированным циклом называется замкнутый путь. Число ребер в пути (цикле) называется длиной пути (цикла), а длина наикратчайшего пути от вершины А до вершины В называется расстоянием от вершины А до вершины В. Расстояние от вершины А до вершины В обозначается S(AB).
Ориентированный граф, у которого любые две различные вершины соединены одним и только одним ребром, называется полным ориентированным графом.
Любой граф, вершины которого пронумерованы от 1 до n, называется помеченным. Любой помеченный граф может быть изображен матрицей смежности, элемент aij которой равен в случае неориентированного графа числу ребер, соединяющих вершины с номерами i и j, а в случае ориентированного графа числу ребер, выходящих из вершины с номером i и входящих в вершину с номером j. Например, изображенным ниже неориентированному и ориентированному графам будут соответствовать следующие матрицы смежности.
1 0 0 0
|
|
|
| |
|
|
1 0 0
| |
Задачи 631 – 640:
631)Пусть помеченный граф Гn содержит n вершин, причем вершины с номерами
i и j соединены ребром в том случае, если номера i и j - взаимно простые числа. Изобразить графы Г4 и Г5 и найти их матрицы смежности.
632)Граф Г имеет пять вершин; В – одна из его вершин, Г - дополнение графа Г.
Какова степень вершины В в графе Г , если в графе Г эта вершина: 1) принадлежит одному ребру;
2) принадлежит трем ребрам.
В каждом случае нарисовать примеры графов Г и Г , а также найти их матрицы смежности для одного из вариантов нумерации вершин.
633)Существует ли граф с пятью вершинами, сумма степеней которых равна
1) 1;
2) 2;
3) 3;
4) 10;
5) 30 ?
Нарисовать пример такого графа, если он существует, и найти его матрицу смежности для одного из вариантов нумерации вершин.
634)Существует ли граф с шестью вершинами, у которого число нечетных вершин равно:
1) 1;
2) 2;
3) 3;
4) 6 ?
Нарисовать пример такого графа, если он существует, и найти его матрицу смежности для одного из вариантов нумерации вершин.
635)Существует ли граф с пятью вершинами, степени которых равны:
1) 1, 2, 2, 2, 3;
2) 0, 2, 2, 3, 4;
3) 1, 2, 2, 3, 4;
4) 1, 2, 2, 3, 3 ?
Нарисовать пример такого графа, если он существует, и найти его матрицу смежности для одного из вариантов нумерации вершин
636)Существует ли граф с шестью вершинами, степени которых равны:
1) 1, 2, 2, 2, 3, 5;
2) 0, 1, 2, 2, 3, 4;
3) 1, 1, 2, 2, 3, 3 ?
Нарисовать пример такого графа, если он существует, и найти его матрицу смежности для одного из вариантов нумерации вершин
637). Можно ли назвать граф, изображенный на рисунке,
 |
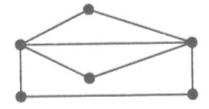1) эйлеровым графом;
2) гамильтоновым графом?
Найти матрицу смежности для одного из вариантов нумерации вершин.
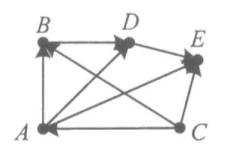
638)Для ориентированного графа, изображенного на рисунке:
1) определить степень входа и степень выхода каждой вершины;
2) найти источник и сток;
3) найти все пути из вершины C в вершину D;
4) определить расстояние от вершины С до вершины D;
5) указать вершину, которая не достижима ни из одной вершины;
6) найти матрицу смежности для нумерации вершин в порядке следования букв в алфавите.
639)Нарисовать ориентированный граф с шестью вершинами, который имеет:
1) ровно два стока и четыре источника;
2) ровно два источника и четыре стока; Какое наименьшее число ребер имеет такой граф?
Для нарисованных графов найти матрицы смежности, используя один из вариантов нумерации вершин.
640)Дан полный ориентированный граф с пятью вершинами. Сумма степеней входа первых четырех вершин равна 9, а их сумма степеней выхода равна 7. Найти степень входа и степень выхода пятой вершины этого графа. Нарисовать граф, удовлетворяющий условиям задачи, и найти матрицу смежности для одного из вариантов нумерации вершин.