Прикладная информатика в экономике
Томск
ТУСУР
Электронное пособие составлено и скорректировано с учётом реального проведения лекций на ФСУ в гр. 446-1-2 весной 2017 года.
Оглавление по темам
ГЛАВА 1. ИНТЕГРАЛЫ. 5
§1. Определения и основные методы. 5
§2. Интегрирование рациональных дробей. 11
§3. Интегрирование иррациональностей и тригонометрических выражений. 17
§4. Определённый интеграл и его приложения. 27
§5. Несобственный интеграл. 38
§6. Кратные интегралы. 46
ГЛАВА 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. 60
§ 1. Дифференциальные уравнения 1-го порядка. 60
§ 2. Дифференциальные уравнения порядка n. 70
§ 3. Линейные дифференциальные уравнения порядка n. 74
§ 4. Системы дифференциальных уравнений. 87
§ 5. Комплексные числа, их связь с дифф.уравнениями. 90
ГЛАВА 3. РЯДЫ. 104
§ 1. Числовые ряды. 104
§ 2. Функциональные ряды. 117
§ 3. Степенные ряды. 120
§ 4. Ряды Тейлора и Лорана. 126
§ 5. Ряды Фурье.
Оглавление по номерам лекций
Лекция 1. 14.02.2017 5 - 15
Лекция 2. 21.02.2017 16 - 26
Лекция 3. 28.02.2017 27 - 38
Лекция 4. 07.03.2017 38 - 49
Лекция 5. 14.03.2017 50 - 59
Лекция 6. 21.03.2017 60 - 69
Лекция 7. 28.03.2017 70 - 79
Лекция 8. 04.04.2017 79 - 89
Лекция 9. 11.04.2017 90 - 101
Лекция 10. 18.04.2017 102 -114
Лекция 11. 25.04.2017 115 -125
Лекция 12. 02.05.2017 126 -134
Лекция 13. 16.05.2017
Лекция 14. 23.05.2017
Лекция 15. 30.05.2017
Приложение 1.Вопросы на доказательства. 135
Приложение 2. Мелкие и устные вопросы на знание теории
(для коллоквиумов). 140
Приложение 3. Задачи из лекций. 144
ЛЕКЦИЯ № 1. 14. 02. 2017
ГЛАВА 1. ИНТЕГРАЛЫ.
Определения и основные методы.
Определение. Если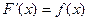 
, то 
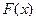называется первообразной от функции 
.
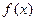Свойство.Если 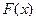первообразная, то 
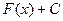(для любого 
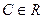) тоже является первообразной для той же самой функции .
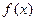Это легко доказать, действительно,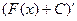 
= 
= .
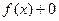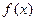Таким образом, первообразных бесконечно много, то есть, если поднять или опустить на любую высоту график 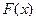, снова будет первообразная.
Свойство.Есл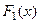и 
и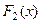 
две различные первообразные функции 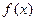, то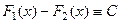 
.
Доказывается так: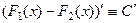 
, то есть 
.
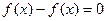Определение. Множество всех первообразных от одной и той же функции 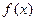называется неопределённым интегралом этой функции.
Обозначение: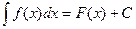 
.
Свойства линейности.
1. 
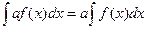
2. 
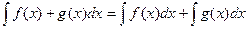
Замечание.
Для произведения свойство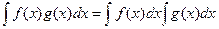 
не существует. Чтобы убедиться в этом, достаточно рассмотреть любые 2 простейшие функции, например 
, 
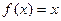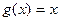. Тогда:
= 
= 
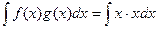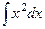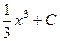, в то же время
= 
= 
.
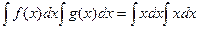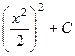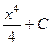Впрочем, можно даже рассмотреть 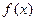произвольную, 
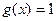. Тогда 
,
= 
.
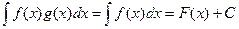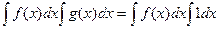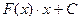Таблица основных интегралов.
( 
)
; 
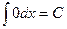
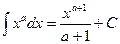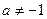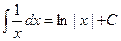
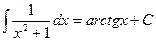
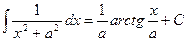
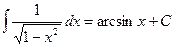
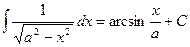
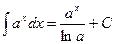
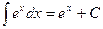
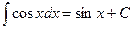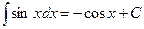
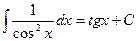
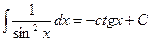
Объяснение причины возникновения модуля в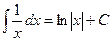 
. Функция 
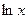существует только на правой полуоси, тогда как 
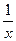имеет две ветви, на правой и левой полуоси. Получалось бы противоречие, что производная от несуществующей функции есть на левой полуоси. Функция 
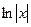является чётным продолжением 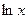на левую полуось, и именно она там является первообразной для 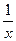при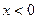 
.
Методы интегрирования.
1. Преобразования подынтегральных выражений.
Различные преобразования, например, арифметические (домножить и поделить, прибавить и отнять), выделение полного квадрата, разбиение многочлена на множители, преобразования по тригонометрическим формулам, и т.д. нередко помогают упростить исходное выражение, разбить его на несколько более простых слагаемых, которые уже сводятся к интегралам табличного типа. На практике рассмотрены разнообразные примеры на виды этих преобразований. Часто нужно домножить и поделить, чтобы сформировать готовое выражение, являющееся производной от известной функции. Например,
Пример. =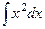 
= .
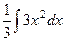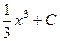Когда сформировали выражение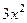 
, а заодно поделили на 3 перед интегралом, теперь уже точно невозможно перепутать или забыть коэффициент.
Аналогично, допустим, что мы помним, что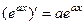 
. Тогда можно постараться сформировать готовое выражение типа 
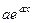внутри интеграла. Тем самым мы автоматически докажем, что при интегрировании такое выражение на этот коэффициент делится, а не домножается:
Пример.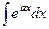 
= 
= 
.
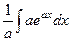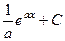Тригонометрические преобразования:
Пример. Вычислить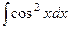 
.
Решение. Применим формулу понижения степени.
= 
= 
=
= 
.
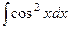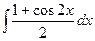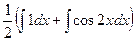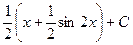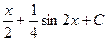Пример. Вычислить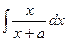 
.
Решение. =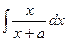 
= 
=
= 
.
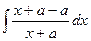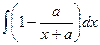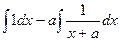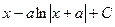Ответ. .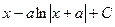
Замена переменной.
Бывают такие случаи, когда функция имеет вид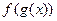 
, то есть явно видно, что всё выражение зависит от какого-то однотипного блока, например всё выражается через 
или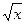 
. Делается замена на 
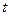, только нужно не забыть пересчитать 
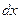, потому что 
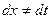, если только замена не является простым линейным сдвигом 
.
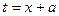Пример. Вычислить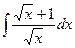 
.
Решение. Сделаем замену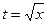 
, тогда 
, 
, 
.
= 
= 
= 
.
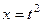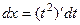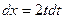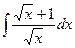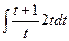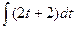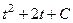Обратная замена: =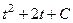 
= 
.
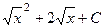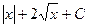Более того, область определения исходной функции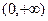 
из-за наличия в ней квадратного корня, точка 0 не входит в область определения, так как корень там и в знаменателе, так что знак модуля в ответе является излишним, ответ можно записать так: 
.
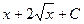Если в функции присутствуют корни разного порядка, например 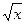и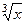 
, то замена должна происходить через корень порядка НОК (наименьшее общее кратное). Причина в том, что именно при этом все корни переводятся в целые степени от .
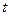Если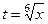 
, тогда: 
, 
.
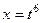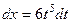Объяснение, почему все корни выразятся через целые степени :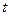
= 
,
= 
.
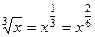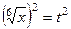
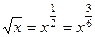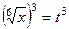