Экономико-математическая модель.
o Найти план (количество хлеба и батонов) такой, чтобы
o Прибыль =0,99*Хлеб+1,21*Батон –Хлеб^0,7-Батон^0,7 - mах
o При ограничениях:
0,6*Хлеб+0,5*Батон<=120
0,05*Хлеб+0,08*Батон<=70
0,2*Хлеб+0,6*Батон<=65
0,2*Хлеб+0,24*Батон<=50
Хлеб,Батон>=0
Реализация в Excel.
Создаем таблицу с формулами, которые связывают план, ограничения и целевую функцию (Прибыль):
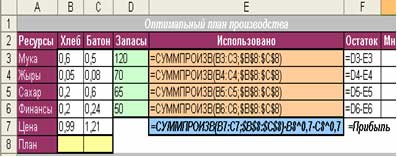
· в столбце «Использовано» в каждую ячейку вводим формулу вычисления количества использованных ресурсов: =СУММПРОИЗВ(Норма; План);
· в ячейку с Прибылью вводим формулу =СУММПРОИЗВ(Цена; План)- Хлеб^0,7-Батон^0,7.
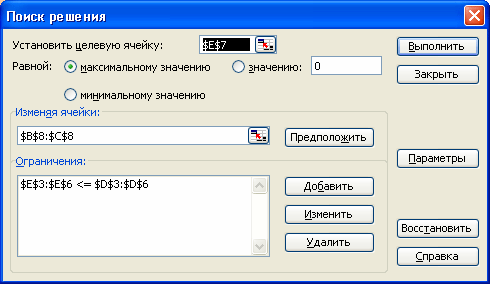
Запускаем программу Поиск решений командой Данные/Анализ/Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Неотрицательные значения. Нажимаем кнопку Выполнить и в появившемся окне Результаты поиска решения выводим отчет по устойчивости.
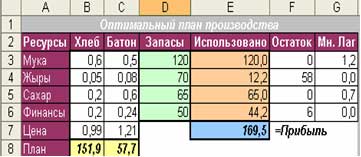
Анализ результата.
Оптимальный план производства (151,9; 57,7) обеспечивает максимальную прибыль в размере 169,5 д. ед.
Множители Лагранжа указывают на увеличения прибыли при увеличении дефицитного запаса ресурсов на 1 ед.
Практическая задача №2 нелинейной модели.
Управление запасами
Постановка задачи.
За статистикой средние затраты на содержания запасов составляют почти треть стоимости этих запасов. Это очень много, и это показатель растет с усложнением современного производства, где номенклатура всего, что используется, измеряется десятками и сотнями тысяч наименований, и поэтому очень высокий риск сбоя или остановки производства из-за отсутствия хотя бы одной составляющей.
Запасы на производстве – это предметы, которые стают частью продукции или вносят вложение у производство: сырье, готовая продукция, комплектующие, вспомогательные материалы и т. д. Запас у сфере услуг (магазин, салоны, почта, банки, рестораны, службы проката и т. д.) – это товары на продажу, запасные части, деньги, еда, транспортные средства, аттракционы.
Если запасов много, это, одновременно хорошо (надежно обеспечивается спрос) и плохо (большие затраты на хранение) – потому должна быть «золотая середина» у виде оптимального запаса.
Оптимально управлять запасом – значит, определить такие моменты и объемы поставки для пополнения запасов, что бы минимизировать общие затраты на создание и получение запасов соответственно с их использованием (спрос).
Предположение: фиксированный размер заказа; стабильные спрос; мгновенное пополнения запаса; отсутствия дефицита на готовую продукцию.
Впервые эту модель определил Р. Уильсон (R. H. Wilson) в 1927 году и носит название «формула Уильсона»:
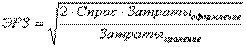
В англоязычной литературе оптимальный запас называется экономический размер заказа, ЭРЗ (Economic Order Quantity, EOQ).
В нашем случае нужно определить оптимальный размер заказа четырех товаров, для каждого и них известны цены для покупки, спрос, затраты на оформление и хранение единицы продукции, а также ограничении на размер склада и суму финансирования покупки.
Экономико-математическая модель.
1. Найти оптимальный план заказа, чтобы
2. Общие затраты = Затраты на оформление + Затраты на хранение - min
3. При ограничениях: Занятая площадь на складе <= Площадь склада; Финансирования покупки <= Бюджет; План >= 0.
Реализация в Excel.
Создаем таблицу с формулами, которые связывают план, ограничения и целевую функцию (ОЗ):
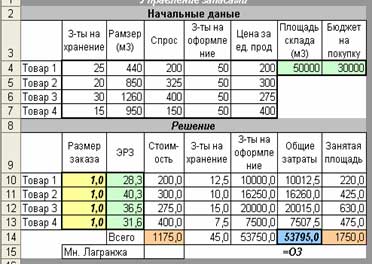
· в столбец ЭРЗ (экономический размер заказа) вводим формулы Уильсона;
· столбец Стоимость вводим формулы: Размер заказа * Цена;
· в столбец Затраты на хранение вводим формулы: (Размер заказа * Затраты на хр.)/2;
· в столбец Затраты на оформление вводим формулы: (Затраты на оформ. * Спрос)/ Размер заказа;
· в столбец Общие затраты вводим формулы сумы столбцов Затраты на хранение и оформление;
· столбец Занятая площадь заполняем формулами: (Размер заказа * Размер товара)/2;
· в строку Всего вводим формулы сумы по соответствующим столбцам.
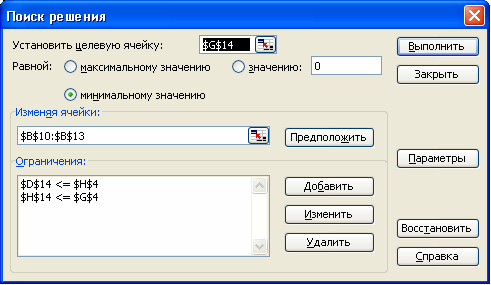
Запускаем программу Поиск решений командой СДанные/Анализ/Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Неотрицательные значения. Нажимаем кнопку Выполнить и в появившемся окне Результаты поиска решения выводим отчет по устойчивости.
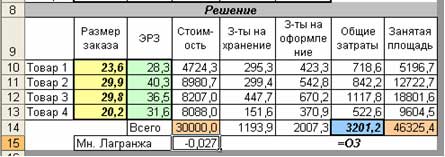
Анализ результата.
Размеры полученных заказов меньше оптимальных (ЭРЗ), поскольку они ограничены бюджетом финансирования покупки товаров. Множитель Лагранжа указывает на возможность уменьшения общих затрат при увеличении бюджета.
Заключение
Многие задачи, с которыми приходится сталкиваться экономисту в повседневной практике при анализе хозяйственной деятельности предприятий, многовариантны. Так как не все варианты одинаково хороши, среди множества возможных приходится отыскивать оптимальный. Значительная часть подобных задач на протяжении долгого времени решалась исходя из здравого смысла и опыта. При этом не было никакой уверенности, что найденный вариант является наилучшим.
В современных условиях даже не значительные ошибки могут привести к огромным потерям. В связи с этим возникла необходимость привлечения к анализу и синтезу экономических систем оптимизационных экономико-математических методов и ЭВМ, что создает основу для принятия научно обоснованных решений. Такие методы объединяют в одну группу под общим названием «оптимизационные методы анализа и принятия решения в экономике».
Чтобы решить экономическую задачу математическими методами, прежде всего необходимо построить адекватную ей математическую модель, т.е. формализовать цель и условия задачи в виде математических функций, уравнений и (или) неравенств.
Из данной курсовой работы стало ясно, что внедрение экономико-математических методов помогает совершенствовать анализ финансового-хозяйственной деятельности. Их применение повышает эффективность экономического анализа за счет расширения факторов, обоснования принимаемых управленческих решений, выбора оптимального варианта использования хозяйственных ресурсов, выявления и мобилизации резервов повышения эффективности производства.
Список используемой литературы:
1. Басовский Л.Е. Теория анализа хозяйственной деятельности. М.: ИНФРА-М, 2001г.
2. Савицкая Г. В. Экономический анализ. М.: Новое издание, 2004г.
3. Шеремет А. Д. Теория экономического анализа. М.: ИНФРА-М, 2002г
4. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем; Учебное пособие. – М.: Финансы и статистика. 2003. – 368 с.
5. Бережной В.И., Бережная Е.В. Экономико-математические методы и модели в примерах и задачах. – Ставрополь: Интеллект-сервис. 1996. – 188 с.
6. Советов Б.Я., Яковлев С.А. Моделирование систем:Учебное пособие для втузов – 3-е изд., перераб. и доп. – М.: Высшая школа, 2001. –343 с.
7. Белобродский-Гриценко. Поиск решений с Excel 2000 - Руководство по решению экстремальных задач в экономике - 2003 – 76 с.
