Бисериальный коэффициент корреляции

В тех случаях, когда одна переменная измеряется в дихотомической шкале (переменная X),а другая в шкале интервалов или отношений (переменная Y),используется бисериальный коэффициент корреляции. Например, при проверке гипотез о влиянии пола ребенка на показатель роста и веса.

Коэффициент изменяется в диапазоне от - 1 до +1, но его знак для интерпретации результатов не имеет значения. Для применения бисериального коэффициента корреляции необходимо соблюдать следующие условия:

1. Сравниваемые признаки должны быть измерены в разных шкалах: одна X – в дихотомической шкале; другая Y – в шкале интервалов или отношений.

2. Переменная Y имеет нормальный закон распределения.

3. Число варьирующих признаков в сравниваемых переменных X
и Y должно быть одинаковым.

Если же переменная X измерена в дихотомической шкале, а переменная Y в ранговой шкале (переменная Y), то можноиспользовать рангово-бисериальный коэффициент корреляции. Этот коэффициент тесно связан с τ-Кендалла и использует в своем определении понятия совпадения и инверсии. Интерпретация результатов та же, что и для бисериального коэффициента корреляции.

Пусть переменная X измерена в сильной шкале, а переменная Y – в дихотомической. Точечный бисериальный коэффициент корреляции rpb вычисляется по формуле:

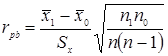
Здесь x₁ – среднее значение по Х объектов со значением «единица» по Y;

x₀ – среднее значение по Х объектов со значением «ноль» по Y;

s_х – среднее квадратическое отклонение всех значений по Х;

n₁ – число объектов «единица» по Y, n₀ — число объектов «ноль» по Y;

n = n₁ + n₀ – объем выборки.

Точечный бисериальный коэффициент корреляции можно рассчитать также с помощью других эквивалентных выражений:

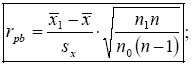
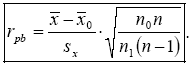
Здесь x – общее среднее значение по переменной Х.

Точечный бисериальный коэффициент корреляции rpb изменяется в пределах от –1 до +1. Его значение равно нулю в том случае, если пере-менные с единицей по Y имеют среднее по Y, равное среднему переменных с нулем по Y.

Проверка гипотезы о значимоститочечного бисериального коэффициента корреляции заключается в проверке нулевой гипотезы h0 о равенстве генерального коэффициента корреляции нулю: ρ = 0, которая осуществляется с помощью критерия Стьюдента. Эмпирическое значение

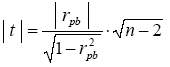
сравнивается с критическими значениями t_a(df) для числа степеней свободы df = n – 2

Если выполняется условие | t | ≤ tα(df), нулевая гипотеза ρ = 0 не от-вергается. Точечный биссериальный коэффициент корреляции значимо от-личается от нуля, если эмпирическое значение | t | попадает в критическую область, то есть если выполняется условие | t | > tα(n – 2). Достоверность связи, рассчитанной с помощью точечного бисериального коэффициента корреляции rpb, можно определить также с помощью критерия χ2 для числа степеней свободы df = 2.

Пример вычисления бисериального КК.

Пусть переменная х – это рост в см, а переменная у – это пол (1 – мальчики, 0 – девочки). В эксперименте участвовали 15 подростков. Были получены следующие результаты:

х	у
150 170 160 165 140 183 157 152 163 168 180 155 157 160 152	1 0 1 1 0 1 0 0 1 1 1 0 1 0 0

n = 15 n1 = 8 n0 = 7
x 1 = (150+160+…+157) : 8 = 163,25
x 0 = (170+140+…+152) : 7 = 156,57
x = 8,94
rpb = (163,25 – 156,57) : 8,94 8 7; (15 (15 – 1)) = 0,41
n = 15 = 0,05
tнабл = n – 2 rpb : 1 – rpb = 15 – 2 0,41 : 1 – (0,41) = 1,62
/2 = 0,05/2 = 0,025 = n – 2 = 15 – 2 = 13 tкр = 2,16