Проверка значимости коэффициента корреляции

Так как выборочный коэффициент 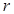вычисляется по выборочным данным, то он является случайной величиной.Если 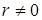, то возникает вопрос: объясняется ли это действительно существующей линейной связью между 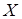и и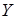ли вызвано случайными факторами?

Проверим нулевую гипотезу о том, что в генеральной совокупности отсутствует корреляция 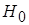: 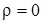, а отличие от нуля выборочного коэффициента корреляции объясняется только случайностью выборки.

Альтернативная гипотеза может быть одной из видов: двусторонней 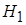: 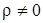(если не известен знак корреляции); или односторонне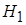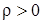й : или 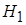: 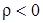(если знак корреляции может быть заранее определен).

Способ 1. Для проверки гипотезы используется 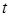-критерий Стьюдента. Вычисляется эмпирическое значение 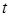-критерия Стьюдента по формуле

,

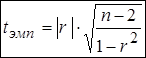где 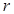- выборочный коэффициент корреляции, 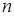- объем выборки.

Вычисленное эмпирическое значение 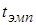сравнивается с найденным по таблице критическим значением 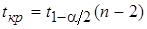при выбранном уровне значимости 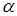и числе степеней свободы 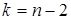для двустороннего критерия.

Критическая область задается неравенством .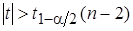

Если 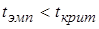, то принимается нулевая гипотеза. Значит, в генеральной совокупности отсутствует значимая корреляция, а отличие от нуля выборочного коэффициента корреляции объясняется только случайностью выборки.

Если 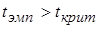, то нулевая гипотеза отклоняется. Делаем выводы:

§ для двусторонней альтернативной гипотезы – коэффициент корреляции значимо отличается от нуля;

§ для односторонней гипотезы – существует статистически значимая положительная (или отрицательная) корреляция.

Способ 2. Можно воспользоваться такжетаблицей критических значений коэффициента корреляции, из которой находим величину критического значения коэффициента корреляции 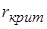по числу степеней свободы 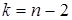и уровню значимости .

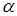Если 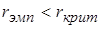, то в генеральной совокупности отсутствует значимая корреляция между исследуемыми признаками, а отличие от нуля выборочного коэффициента корреляции объясняется только случайностью выборки либо объем выборки недостаточен для выявления линейной связи.

Если же 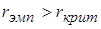, то делается вывод, что коэффициент корреляции значимо отличатся от 0 и существует статистически значимая корреляция.

Так, одни явления могут одновременно, но независимо друг от друга (совместные события) происходить или изменяться (ложная регрессия). Другие – находиться в причинной зависимости не друг с другом, а по более сложной причинно-следственной связи (косвенная регрессия). Таким образом, при значимом коэффициенте корреляции окончательный вывод о наличии причинно-следственной связи можно сделать только с учетом специфики исследуемой проблемы.

Лекция 12. коэффициенты ранговой корреляции и ассоциации

1. Коэффициент ранговой корреляции 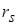Спирмена