Многоканальная СМО с неограниченной очередью

Имеется n-канальная СМО с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность 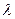, а поток обслуживаний – интенсивность 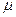. Необходимо найти предельные вероятности состояний СМО и показатели ее эффективности.

Система может находиться в одном из состояний s₀, s₁, s₂,…,s_k,…,s_n, нумеруемых по числу заявок, находящихся в СМО: s₀ – в системе нет заявок (все каналы свободны); s₁ – занят один канал, остальные свободны; s₂ – заняты два канала, остальные свободны;…; s_k – занято k каналов, остальные свободны;…; s_n – заняты все n каналов (очереди нет); s_n+1 – заняты все n каналов, в очереди одни заявка;…; s_n+r – заняты все n каналов, r заявок в очереди.

Граф состояний приведен на рис. 7

… …

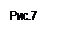
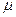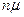В отличие от одноканальной СМО интенсивность потока обслуживаний не остается постоянной, а по мере увеличения числа заявок в СМО от 0 до n увеличивается от величины до , т.к. соответственно увеличивается число каналов обслуживания. При числе заявок больше, чем n, интенсивность потока обслуживаний сохраняется равной 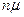. Если в системе n каналов обслуживания с интенсивностью 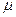, интенсивность входящего потока равна 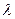, то, чтобы очередь не стала бесконечно большой, необходимо выполнение условия стационарности

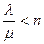
Это условие означает, что суммарная скорость обслуживания всех каналов системы 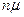должна превосходить скорость поступления требований 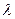, иначе система не справится с обслуживанием потока.

Данное условие характерно только для систем с очередью в отличие от систем с отказом, т.к. все поступившие требования должны получить обслуживание.

Используя формулы (11)для процесса гибели и размножения, можно получить формулы для предельных вероятностей состояний n-канальной СМО с неограниченной очередью

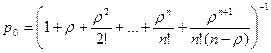(31)

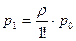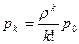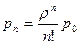,…, ,…, (32)

,…,

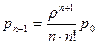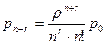
Вероятность того, что в системе заняты обслуживанием все n каналы, определяется по формуле

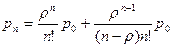(33)

Для n-канальной СМО с неограниченной очередью, используя прежние приемы, можно найти:

- среднее число занятых каналов

,

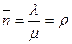- среднее число заявок в очереди

,

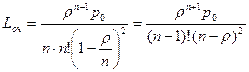- среднее число заявок в системе

,

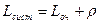- среднее время обслуживания заявки

,

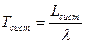- среднее время ожидания обслуживания

.

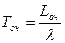Полученные выше формулы значительно упрощаются в случае одно – или двухканальной системы

При n=1

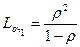, т.к.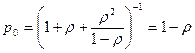

;

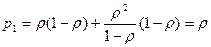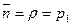
При n=2

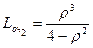, т.к.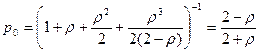

,

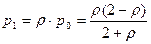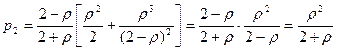
Пример 7. К двум продавцам поступает на обслуживание поток покупателей с интенсивностью 220 человек в час. Каждый из продавцов затрачивает на обслуживание покупателя в среднем 30 секунд. Определите среднюю длину очереди и показатели занятости продавцов.

Решение. , ,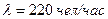

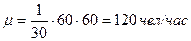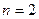
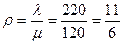– интенсивность загрузки

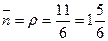– среднее число занятых обслуживанием каналов

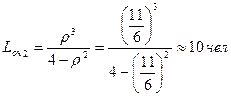– средняя длина очереди

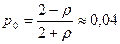– доля времени простоя продавцов

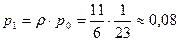– доля времени занятости одного из двух продавцов

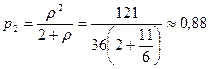– доля времени занятости двух продавцов

Пример 8. В универсаме к узлу расчета поступает поток покупателей с интенсивностью 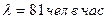. Средняя продолжительность обслуживания контролером-кассиром одного покупателя 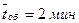. Определить минимальное количество контролеров-кассиров n_мин, при котором очередь не будет расти до бесконечности и соответствующие характеристики обслуживания при n=n_мин.

Решение. По условию 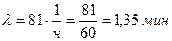, 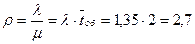. Очередь не будет возрастать до бесконечности при условии 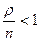, т.е. при 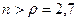. Таким образом, минимальное количество контролеров-кассиров n_min=3.

Вероятность того, что в узле расчета отсутствуют покупатели, по формуле (31)

,

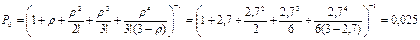т.е. в среднем 2,5% времени контролеры-кассиры будут простаивать.

Среднее число покупателей, находящихся в очереди равно

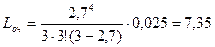
Среднее время ожидания в очереди

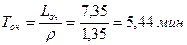
Среднее число покупателей в узле расчета

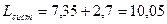
Среднее время нахождения покупателей в узле расчета

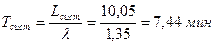
Среднее число контролеров-кассиров, занятых обслуживанием покупателей

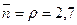
Отметим, что для СМО с неограниченной очередью при 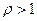любая заявка, пришедшая в систему, будет обслужена, т.е. вероятность отказа Р_отк=0, относительная пропускная способность Q=1, а абсолютная пропускная способность равна интенсивности входящего потока заявок, т.е. .

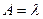Для нашей задачи абсолютная пропускная способность узла расчета A=1,35 1/мин или 81 1/ч, т.е. 81 покупатель в час.

Анализ характеристик обслуживания свидетельствует о значительной перегрузке узла расчета при наличии трех контролеров-кассиров.