Основные непрерывные распределения

Равномерное распределение

СВ X распределена равномерно на отрезке , т.е. , если её плотность распределения имеет вид

(2.8)

а функция распределения определяется выражением

(2.9)

Графики плотности и функции распределения представлены на рисунках

Математическое ожидание и дисперсия равномерно распределённой величины определяются следующими выражениями:

(2.10)

(2.11)

Равномерное распределение является непрерывным аналогом дискретного распределения вероятностей для опытов с равновероятными исходами.

СВ X, являющаяся погрешностью приближенных вычислений каких-либо параметров при округлении до ближайших целых чисел, удовлетворительно описывается распределением .

Экспоненциальное распределение

СВ X имеет экспоненциальное (показательное) распределение с параметром , т. е. , если её плотность распределения имеет вид

(2.12)

а функция распределения определяется выражением

(2.13)

Графики плотности и функции распределения представлены на рисунках

Математическое ожидание и дисперсия равномерно распределённой величины определяются следующими выражениями:

(2.14)

(2.15)

Экспоненциальное распределение является одним из основных распределений, используемых в теории надежности для описания времени безотказной работы технических объектов.

Интервал времени между событиями в пуассоновском потоке – случайная величина, распределённая по экспоненциальному закону. Действительно, вероятность того, что на временном интервале 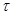в пуассоновском потоке не произойдёт ни одного события определяется из соотношения:

С другой стороны это вероятность того, что время между событиями в пуассоновском потоке превысит величину 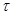: Следовательно, , а это выражение представляет собой экспоненциальную функцию распределения случайной величины :

.

Нормальное распределение

СВ X имеет нормальное (гауссовское) распределение с параметрами т и , т.е. , если

(2.16)

Рис. 1

При этом СВ называется нормальной (гауссовской). График плотности нормального распределения (рис. 1), называемый кривой Гаусса, имеет единственный максимум в точке .

Свойства нормального распределения

1. Найдем выражение для функции распределения СВ :

(2.17)

Обозначим , тогда . С учетом введенного обозначения

Окончательно получаем

Здесь введено обозначение для функции распределения стандартной нормальной СВ Y~ N(0:1). График функции распределения F(x) представлен на рис. 2.

Рис. 2

Вместо в справочниках встречается также функция Лапласа

Легко убедиться в том, что и .

2. С помощью линейного преобразования нормальное распределение переходит в стандартное нормальное N(0; 1) с функцией распределения .

3. Нормально распределенная СВ с большой вероятностью принимает значения, близкие к своему МО, что описывается «правилом k сигм»:

Нормальное распределение имеет широкое распространение в прикладных задачах. Это связано с тем, что в реальности многие исследуемые СВ являются следствием различных случайных событий. В частности, при достаточно общих предположениях сумма большого числа независимых СВ имеет распределение, близкое к нормальному

Пример Рост людей хорошо описывается нормальным распределением. Это, по-видимому, связано с тем, что на рост влияет суперпозиция разнообразных независимых случайных факторов: климата, экологии, экономических условий, болезней и т.д. Погрешности измерительных приборов в навигационных системах ЛА также хорошо описываются нормальным законом.

Лекция 3. Законы распределения компонент случайного вектора (случайных величин). Корреляционная зависимость. Многомерное нормальное распределение