Основные дискретные распределения

Биномиальное распределение

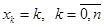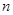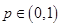Дискретная СВ X с реализациями , имеет биномиальное распределение с параметрами и , что символически записывается как 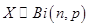, если вероятность события 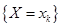определяется формулой Бернулли:

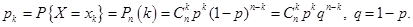(2.1)

Числовые характеристики биномиального распределения:

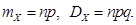(2.2)

Правая часть формулы Бернулли совпадает с выражением для (к + 1) -го слагаемого в разложении бинома Ньютона 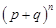, поэтому такое распределение называется биноминальным .

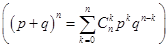Наиболее вероятное значение 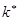биномиально распределённой случайной величины 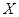удовлетворяет неравенству

.

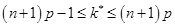Ряд распределения биномиальной величины приведён в таблице

X			…	k	…	n-1	n
P			…		…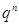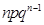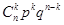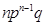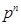

Условия возникновения. Проводится n одинаковых независимых опытов, в каждом из которых событие А появляется с вероятностью р. Случайная величина X - число опытов, в которых произошло событие А (см. теорему о повторении опытов) имеет биномиальное распределение.

Геометрическое распределение

Дискретная СВ X с реализациями 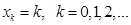, имеет геометрическое распределение с параметром 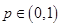, что символически записывается как 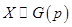, если вероятность события 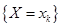определяется формулой:

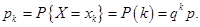(2.3)

Числовые характеристики геометрического распределения:

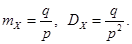(2.4)

Вероятности 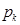образуют геометрическую прогрессию с первым членом 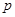и знаменателем 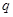, поэтому это распределение называется геометрическим.

Ряд распределения величины, распределённой по геометрическому закону приведён в таблице

X			…	k	…
P			…		…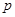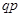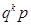

Условия возникновения. Проводится ряд одинаковых независимых опытов до первого появления некоторого события А. Случайная величина X - число проведенных безуспешных опытов до первого появления события А.

Распределение Пуассона

Дискретная СВ X с реализациями 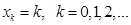, имеет распределение Пуассона с параметром 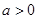, что символически записывается как 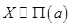, если вероятность события 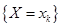определяется формулой:

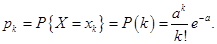(2.5)

Числовые характеристики распределения Пуассона:

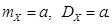(2.6)

Наиболее вероятное значение 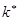пуассоновской случайной величины 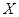удовлетворяет неравенству

.

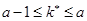На практике СВ имеет, как правило, физическую размерность. В этом случае физические размерност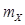и и 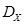не совпадают, хотя их числовые значения для распределения Пуассона равны.

Распределение Пуассона является предельным случаем биномиального, когда число опытов п неограниченно увеличивается 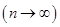, а вероятность р события A в одном опыте стремится к 0 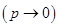, так что существует предел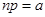

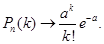
Поэтому при больших 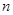и малых 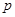двухпараметрическое биномиальное распределение 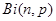можно приближенно заменить однопараметрическим распределением Пуассона 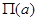, где 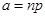. Ошибка от такой замены не превышает :

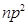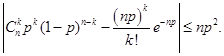
Ряд распределения величины, распределённой по закону Пуассона приведён в таблице

X			…	k	…
P			…		…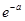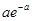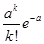

Условия возникновения. Распределение Пуассона широко используется в теории массового обслуживания при описании потоков случайных событий.

Рассмотрим временную ось, на которой будем отмечать моменты возникновения случайных событий (например, отказы компонентов в сложном техническом устройстве, заявки на обслуживание и т.п.). Последовательность таких моментов называется потоком случайных событий.

Поток случайных событий называется стационарным, если число событий, приходящихся на интервал 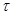, в общем случае не зависит от расположения этого участка на временной оси и определяется только его длительностью, т.е. среднее число событий в единице времени X (интенсивность потока - 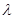) постоянно.

Поток случайных событий называется ординарным, если вероятность попадания в некоторый малый участок 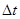двух и более случайных событий значительно меньше, чем вероятность попадания одного события.

В потоке отсутствует последействие, если вероятность попадания событий на участок 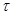не зависит от того, сколько событий попало на другие участки, не пересекающиеся с данным.

Поток случайных событий называется пуассоновским, если он является ординарным и без последействия. Пуассоновский поток случайных событий называется простейшим, если он стационарный.

Распределение событий простейшего потока 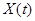с интенсивностью 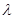на временном интервале длиной 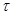является пуассоновским:

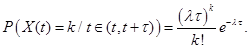(2.7)