Лекция 2. Основные распределения случайных величин.
Лекция 2. Основные распределения случайных величин.
Основные дискретные распределения
Биномиальное распределение
Дискретная СВ X с реализациями 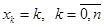 , имеет биномиальное распределение с параметрами
, имеет биномиальное распределение с параметрами 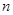 и
и 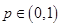 , что символически записывается как
, что символически записывается как 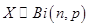 , если вероятность события
, если вероятность события 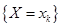 определяется формулой Бернулли:
определяется формулой Бернулли:
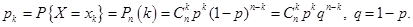 (2.1)
(2.1)
Числовые характеристики биномиального распределения:
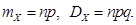 (2.2)
(2.2)
Правая часть формулы Бернулли совпадает с выражением для (к + 1) -го слагаемого в разложении бинома Ньютона 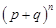 , поэтому такое распределение называется биноминальным
, поэтому такое распределение называется биноминальным 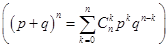 .
.
Наиболее вероятное значение 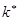 биномиально распределённой случайной величины
биномиально распределённой случайной величины  удовлетворяет неравенству
удовлетворяет неравенству
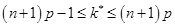 .
.
Ряд распределения биномиальной величины приведён в таблице
| X | … | k | … | n-1 | n | ||
| P | 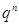 | 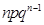 | … | 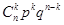 | … | 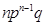 | 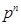 |
Условия возникновения. Проводится n одинаковых независимых опытов, в каждом из которых событие А появляется с вероятностью р. Случайная величина X - число опытов, в которых произошло событие А (см. теорему о повторении опытов) имеет биномиальное распределение.
Геометрическое распределение
Дискретная СВ X с реализациями 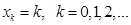 , имеет геометрическое распределение с параметром
, имеет геометрическое распределение с параметром 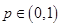 , что символически записывается как
, что символически записывается как 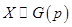 , если вероятность события
, если вероятность события 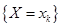 определяется формулой:
определяется формулой:
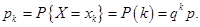 (2.3)
(2.3)
Числовые характеристики геометрического распределения:
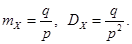 (2.4)
(2.4)
Вероятности 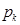 образуют геометрическую прогрессию с первым членом
образуют геометрическую прогрессию с первым членом 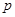 и знаменателем
и знаменателем 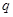 , поэтому это распределение называется геометрическим.
, поэтому это распределение называется геометрическим.
Ряд распределения величины, распределённой по геометрическому закону приведён в таблице
| X | … | k | … | ||
| P | 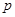 | 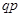 | … | 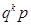 | … |
Условия возникновения. Проводится ряд одинаковых независимых опытов до первого появления некоторого события А. Случайная величина X - число проведенных безуспешных опытов до первого появления события А.
Распределение Пуассона
Дискретная СВ X с реализациями 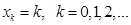 , имеет распределение Пуассона с параметром
, имеет распределение Пуассона с параметром 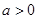 , что символически записывается как
, что символически записывается как 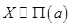 , если вероятность события
, если вероятность события 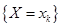 определяется формулой:
определяется формулой:
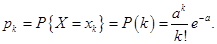 (2.5)
(2.5)
Числовые характеристики распределения Пуассона:
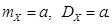 (2.6)
(2.6)
Наиболее вероятное значение 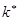 пуассоновской случайной величины
пуассоновской случайной величины 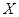 удовлетворяет неравенству
удовлетворяет неравенству
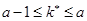 .
.
На практике СВ имеет, как правило, физическую размерность. В этом случае физические размерности 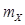 и
и 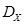 не совпадают, хотя их числовые значения для распределения Пуассона равны.
не совпадают, хотя их числовые значения для распределения Пуассона равны.
Распределение Пуассона является предельным случаем биномиального, когда число опытов п неограниченно увеличивается 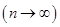 , а вероятность р события A в одном опыте стремится к 0
, а вероятность р события A в одном опыте стремится к 0 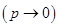 , так что существует предел
, так что существует предел 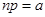
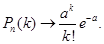
Поэтому при больших 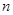 и малых
и малых 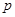 двухпараметрическое биномиальное распределение
двухпараметрическое биномиальное распределение 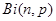 можно приближенно заменить однопараметрическим распределением Пуассона
можно приближенно заменить однопараметрическим распределением Пуассона 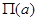 , где
, где 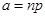 . Ошибка от такой замены не превышает
. Ошибка от такой замены не превышает 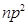 :
:
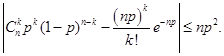
Ряд распределения величины, распределённой по закону Пуассона приведён в таблице
| X | … | k | … | ||
| P | 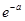 | 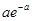 | … | 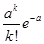 | … |
Условия возникновения. Распределение Пуассона широко используется в теории массового обслуживания при описании потоков случайных событий.
Рассмотрим временную ось, на которой будем отмечать моменты возникновения случайных событий (например, отказы компонентов в сложном техническом устройстве, заявки на обслуживание и т.п.). Последовательность таких моментов называется потоком случайных событий.
Поток случайных событий называется стационарным, если число событий, приходящихся на интервал 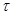 , в общем случае не зависит от расположения этого участка на временной оси и определяется только его длительностью, т.е. среднее число событий в единице времени X (интенсивность потока -
, в общем случае не зависит от расположения этого участка на временной оси и определяется только его длительностью, т.е. среднее число событий в единице времени X (интенсивность потока - 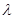 ) постоянно.
) постоянно.
Поток случайных событий называется ординарным, если вероятность попадания в некоторый малый участок 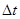 двух и более случайных событий значительно меньше, чем вероятность попадания одного события.
двух и более случайных событий значительно меньше, чем вероятность попадания одного события.
В потоке отсутствует последействие, если вероятность попадания событий на участок 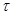 не зависит от того, сколько событий попало на другие участки, не пересекающиеся с данным.
не зависит от того, сколько событий попало на другие участки, не пересекающиеся с данным.
Поток случайных событий называется пуассоновским, если он является ординарным и без последействия. Пуассоновский поток случайных событий называется простейшим, если он стационарный.
Распределение событий простейшего потока 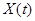 с интенсивностью
с интенсивностью 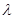 на временном интервале длиной
на временном интервале длиной 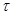 является пуассоновским:
является пуассоновским:
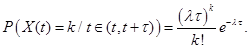 (2.7)
(2.7)
Равномерное распределение
СВ X распределена равномерно на отрезке  , т.е.
, т.е.  , если её плотность распределения имеет вид
, если её плотность распределения имеет вид
 (2.8)
(2.8)
а функция распределения определяется выражением
 (2.9)
(2.9)
Графики плотности и функции распределения представлены на рисунках


Математическое ожидание и дисперсия равномерно распределённой величины определяются следующими выражениями:
 (2.10)
(2.10)
 (2.11)
(2.11)
Равномерное распределение является непрерывным аналогом дискретного распределения вероятностей для опытов с равновероятными исходами.
СВ X, являющаяся погрешностью приближенных вычислений каких-либо параметров при округлении до ближайших целых чисел, удовлетворительно описывается распределением  .
.
Нормальное распределение
СВ X имеет нормальное (гауссовское) распределение с параметрами т и  , т.е.
, т.е.  , если
, если
 (2.16)
(2.16)
 |
Рис. 1
При этом СВ называется нормальной (гауссовской). График плотности нормального распределения (рис. 1), называемый кривой Гаусса, имеет единственный максимум в точке  .
.
Свойства нормального распределения 
1. Найдем выражение для функции распределения СВ  :
:
 (2.17)
(2.17)
Обозначим  , тогда
, тогда  . С учетом введенного обозначения
. С учетом введенного обозначения

Окончательно получаем

Здесь введено обозначение  для функции распределения стандартной нормальной СВ Y~ N(0:1). График функции распределения F(x) представлен на рис. 2.
для функции распределения стандартной нормальной СВ Y~ N(0:1). График функции распределения F(x) представлен на рис. 2.

Рис. 2
Вместо  в справочниках встречается также функция Лапласа
в справочниках встречается также функция Лапласа

Легко убедиться в том, что  и
и  .
.
2. С помощью линейного преобразования  нормальное распределение
нормальное распределение  переходит в стандартное нормальное N(0; 1) с функцией распределения
переходит в стандартное нормальное N(0; 1) с функцией распределения  .
.
3. Нормально распределенная СВ с большой вероятностью принимает значения, близкие к своему МО, что описывается «правилом k сигм»:

Нормальное распределение имеет широкое распространение в прикладных задачах. Это связано с тем, что в реальности многие исследуемые СВ являются следствием различных случайных событий. В частности, при достаточно общих предположениях сумма большого числа независимых СВ имеет распределение, близкое к нормальному
Пример Рост людей хорошо описывается нормальным распределением. Это, по-видимому, связано с тем, что на рост влияет суперпозиция разнообразных независимых случайных факторов: климата, экологии, экономических условий, болезней и т.д. Погрешности измерительных приборов в навигационных системах ЛА также хорошо описываются нормальным законом.
Лекция 3. Законы распределения компонент случайного вектора (случайных величин). Корреляционная зависимость. Многомерное нормальное распределение
Задача композиции.
В одном из важных частных случаев функциональной зависимости 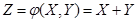 возникает задача определения закона распределения суммы компонент случайного вектора по известному закону совместного распределения его компонент. Если, например,
возникает задача определения закона распределения суммы компонент случайного вектора по известному закону совместного распределения его компонент. Если, например, 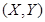 - НСВ с известной плотностью совместного распределения компонент
- НСВ с известной плотностью совместного распределения компонент 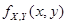 и
и 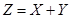 , то
, то
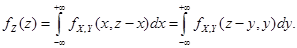 (4.23)
(4.23)
Если 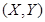 ДСВ, то закон распределения ДСВ
ДСВ, то закон распределения ДСВ 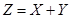 записывается в виде
записывается в виде
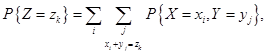
где суммирование распространяется на все значения индексов  и
и  , для которых выполняется условие
, для которых выполняется условие 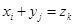 .
.
В частности, если 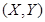 - ДСВ с независимыми компонентами, то
- ДСВ с независимыми компонентами, то
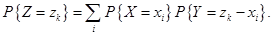 (4.24)
(4.24)
Если 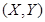 - НСВ с независимыми компонентами, то формула (4.23) приводится к свертке двух плотностей:
- НСВ с независимыми компонентами, то формула (4.23) приводится к свертке двух плотностей:
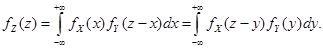 (4.25)
(4.25)
Задача определения закона распределения суммы независимых случайных величин носит название задачи композиции. Описанные выше формулы (4.24) и (4.25) дают непосредственное решение задачи композиции. Формулу (4.25) удобно применять в тех случаях, когда плотности распределения вероятностей компонент описываются одной формулой на всей оси (что, например, справедливо для нормального закона, закона Коши и т.д.). Другой подход к решению задачи композиции основан на применении свойств характеристической функции (см. ниже). Так как 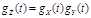 , то, найдя
, то, найдя 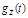 , можно по характеристической функции восстановить закон распределения случайной величины Z.
, можно по характеристической функции восстановить закон распределения случайной величины Z.
Закон распределения W определенного вида называется композиционно устойчивым, если из того, что две независимые случайные величины X и У подчиняются закону распределения данного вида, следует, что их сумма X + Y подчиняются закону распределения W того же вида.
Пример. Доказать композиционную устойчивость нормального закона.
5. Характеристические функции случайных величин.Если 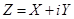 — комплекснозначная случайная величина, где X и Y — действительные случайные величины, то М [Z] = М [X] + i М [У].
— комплекснозначная случайная величина, где X и Y — действительные случайные величины, то М [Z] = М [X] + i М [У].
Характеристической функцией gx(t) случайной величины X называется комплекснозначная неслучайная функция действительного аргумента t определяемая равенством
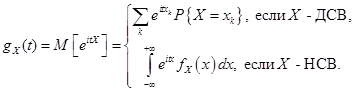
Для НСВ характеристическая функция представляет собой преобразование Фурье от плотности распределения. Поэтому плотность выражается как обратное преобразование Фурье от характеристической функции
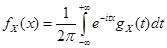
Свойства характеристической функции
-
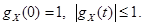
- Если
 - характеристическая функция случайной величины
- характеристическая функция случайной величины 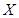 и
и 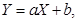 то
то
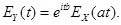
-
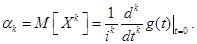
- Если случайные величины
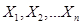 независимы, а
независимы, а 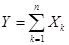 , то
, то
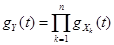
Характеристической функцией случайного вектора 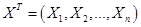 называется комплекснозначная неслучайная функция
называется комплекснозначная неслучайная функция 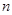 действительных переменных
действительных переменных 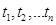 :
:
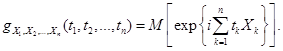
Пример. Найти числовые характеристики 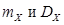 случайной величины
случайной величины 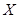 , распределённой по закону Пуассона, используя характеристическую функцию.
, распределённой по закону Пуассона, используя характеристическую функцию.
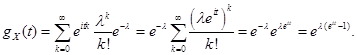
По свойству 3 находим
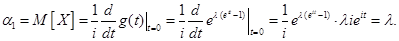
Дисперсию находим по формуле 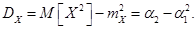
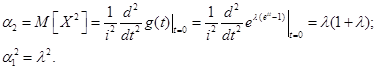
Окончательно находим
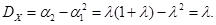
Литература
1. Статистическая динамика и оптимизация управления летательных аппаратов: Учебн. пособие для авиационных специальностей вузов/ А, А. Лебедев, В. Т. Бобронников, М. Н. Красильщиков, В. В. Малышев. – М. Машиностроение, 1985.
2. Вентцель Е. С. Теория вероятностей. – М.: Высшая школа, 1999.
3. Кибзун А. И., Горяинова Е. Р., Наумов А. В., Сиротин А. Н. Теория вероятностей и математическая статистика. – М.: ФИЗМАТЛИТ, 2002.
4. Сборник задач по математике для втузов. Часть 4: /Под общей ред. А. В. Ефимова и А. С. Поспелова. – М.: Изд-во ФИЗМАТЛИТ, 2003.
Лекция 2. Основные распределения случайных величин.
