В гравитационном поле небесного тела

В первом приближении движение искусственного спутника в гравитационном поле притягивающего небесного тела сводится к классической задаче двух тел, в рамках которой притягивающее тело рассматривается как точечный объект, либо, что эквивалентно с точки зрения теории ньютоновского потенциала, как однородный шар. Тогда орбита искусственного спутника лежит в плоскости, занимающей неизменное положение в пространстве, а обращение описывается законами Кеплера и происходит по кеплеровскому эллипсу, не изменяющемуся с течением времени. В реальном случае на спутник действуют возмущающие силы, обусловленные многочисленными факторами гравитационной и негравитационной природы. Доминирующими среди них являются гравитационные возмущения, вызванные отличиями гравитационного поля притягивающего тела от поля притяжения материальной точки (однородного шара).

В прямоугольной геоцентрической средней экваториальной земной системе координат 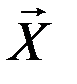уравнение возмущенного движения ИСЗ в согласии со вторым законом Ньютона запишется в виде:

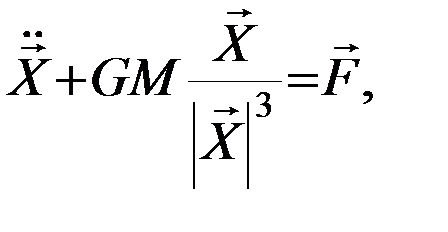
где 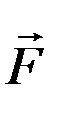- равнодействующая всех сил, возмущающих движение ИСЗ. Понижая порядок этого векторного уравнения, переходим от трех дифференциальных уравнений второго порядка к шести дифференциальным уравнениям первого порядка:

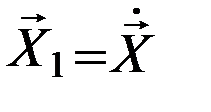(5.3.2)

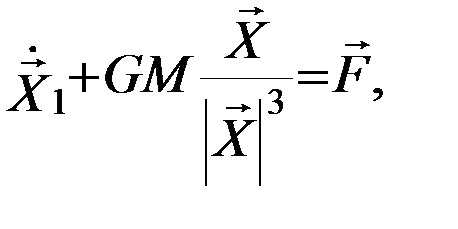
В данный момент важно отметить, что дифференциальные уравнения возмущенного движения, как правило, не интегрируются в аналитическом виде, для применения же численных методов удобнее от декартовой системы координат перейти в систему элементов спутниковой орбиты, в которой по крайней мере пять элементов меняются со временем существенно медленнее, чем вектора положения 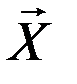и скорости 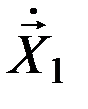ИСЗ. Таким образом, основная идея используемого нами здесь метода Лагранжа состоит в том, чтобы выразить координаты и скорости через элементы орбиты, которые в случае возмущенного движения будут изменяться с течением времени. Такого рода движение в теории Лагранжа принято называть движением по оскулирующему эллипсу. Естественно предположить, что скорость изменения оскулирующих орбитальных элементов будет при этом впрямую зависеть от величины возмущений.

Обозначим элементы оскулирующей орбиты традиционным образом:

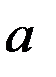· – большая полуось оскулирующего эллипса;

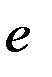· – эксцентриситет эллиптической орбиты;

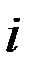· – наклонение плоскости оскулирующей орбиты к проскости экватора;

· – долгота (прямое восхождение) восходящего узла орбиты;

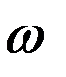· – аргумент перигея, отсчитываемый в плоскости орбиты от восходящего узла до перигея;

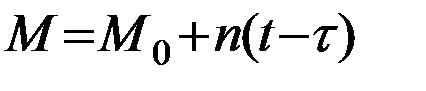· – средняя аномалия, где τ – момент прохождения через перигей, а 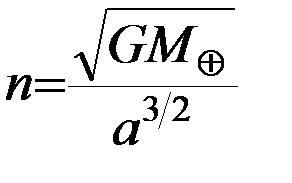-среднее движение. Напомним, что под средней аномалией понимается угол, на который поворачивается за отрезок времени 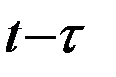радиус-вектор, вращающийся равномерно со средней угловой скоростью n. Иногда вместо M пользуются элементом M₀ , называемым средней аномалией на начальный момент (эпоху) t₀: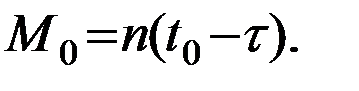

Входящую в (5.3.2) векторную сумму 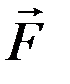возмущающих сил удобно далее разложить по направлению осей правой прямоугольной спутникоцентрической орбитальной системы координат 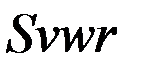, ось 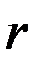которой направлена от центра масс Земли по радиусу вектору ИСЗ, ось 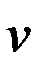устремлена по трансверсали – лежащей в плоскости орбиты спутника нормали к его радиусу вектору, ось 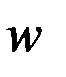- по нормали к плоскости орбиты. Тогда система (5.3.2) двух векторных дифференциальных уравнений первого порядка приводится к системе шести скалярных дифференциальных уравнений, описывающих эволюцию орбиты ИСЗ под действием равнодействующей совокупности 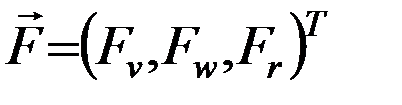возмущающих сил:

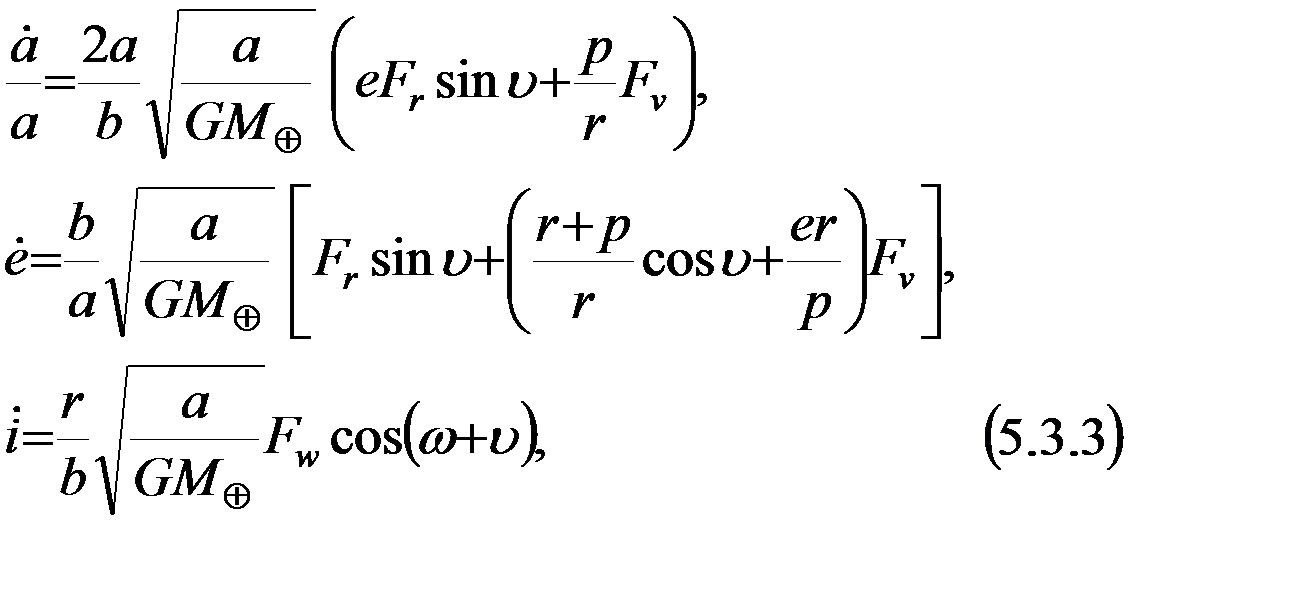
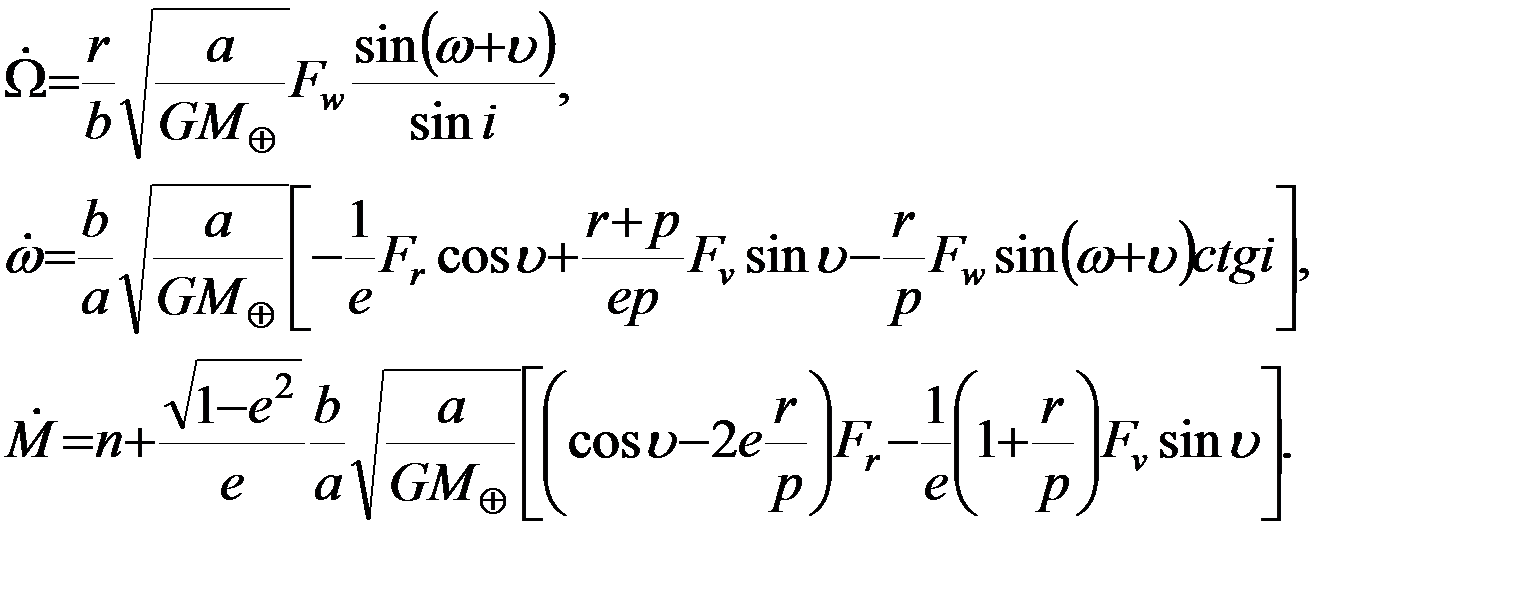
В (5.3.3) принято, что 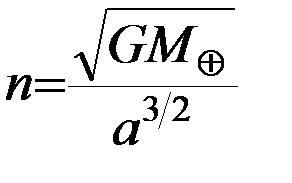-среднее движение.

Уравнения (5.2.3) описывают влияние суммарного вектора 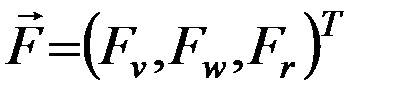возмущающих сил на скорость изменения элементов оскулирующей орбиты ИСЗ и называются уравнениями Ньютона. Рассматривая уравнения Ньютона, можно сделать некоторые замечания о характере изменения элементов орбиты под действием возмущающих сил.

Поскольку вектора ускорени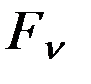й и 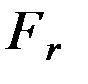лежат в плоскости орбиты, они не могут изменить характеризуемую элементами i и Ω ориентацию плоскости орбиты в пространстве, однако, изменяют остальные четыре элемента. Ускорение 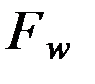перпендикулярно к плоскости орбиты и потому не влияет на эволюцию большой полуоси орбиты 𝑎, но вызывает движение узлов и перигея и изменение наклона орбиты i.

В движении узлов и перигея можно выделить вековые непериодические члены, монотонно изменяющиеся в течение времени, и долгопериодические члены, период которых равен периоду обращения перигея. Члены, период которых зависит от изменений истинной аномалии 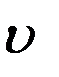, называются короткопериодическими. Из всех возмущений, наблюдаемых в движении спутника, наиболее важными являются два вековых движения: вращение плоскости орбиты вокруг полярной оси (регрессия узлов) и вращение большой полуоси орбиты в ее собственной плоскости (движение перигея). Эти движения могут быть весьма точно определены по наблюдениям ИСЗ.

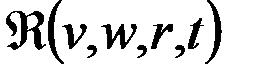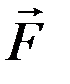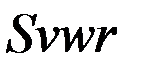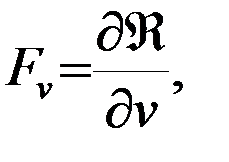
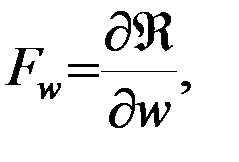
Пусть существует такая возмущающая (пертурбационная) функция , для которой проекции возмущающей силы на оси прямоугольной системы координат определяются формулами: 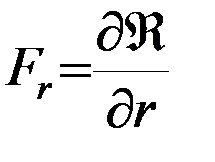, т.е., другими словами, пертурбационная функция представляет собой потенциал возмущающей силы 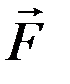. В этом случае указанные проекции в уравнениях Ньютона (5.3.3) могут быть выражены через частные производные пертурбационной функции по элементам оскулирующей орбиты, что позволяет перейти к системе дифференциальных уравнений первого порядка, называемых уравнениями Лагранжа:

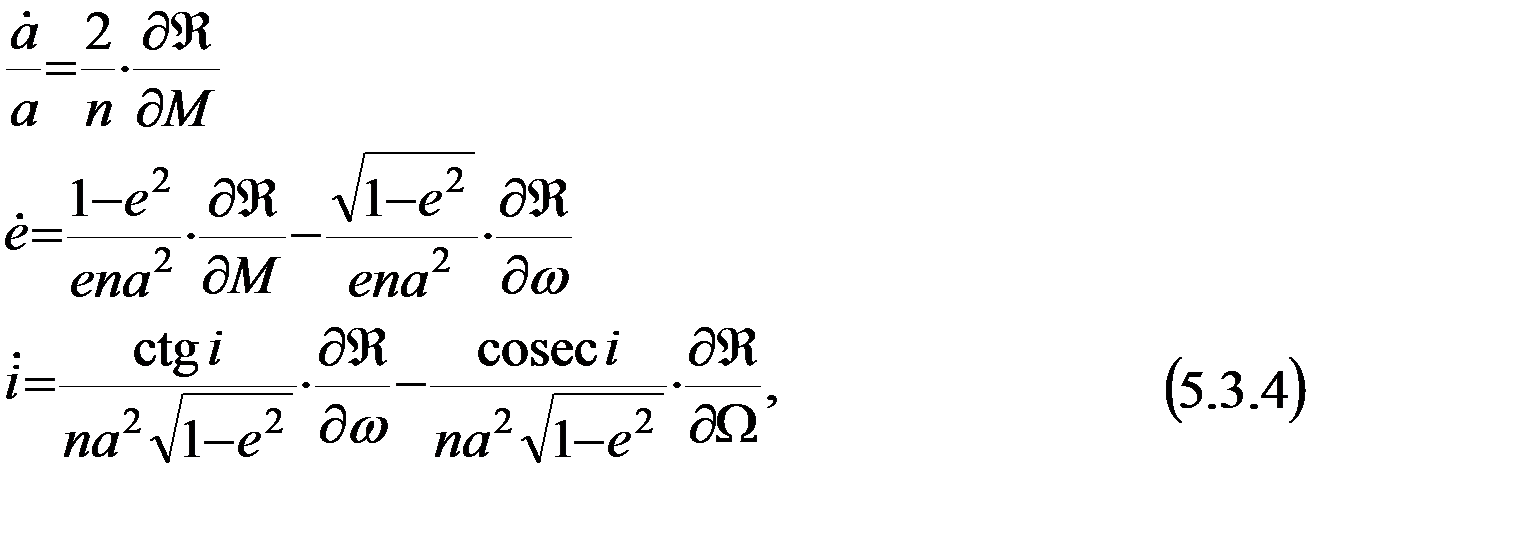
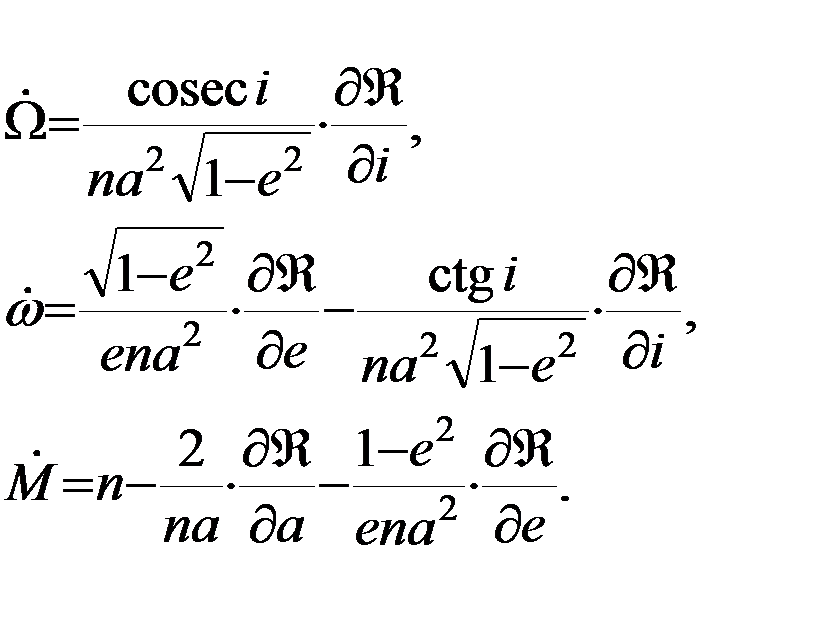
Таким образом, уравнения Лагранжа (5.3.4) описывают связь скорости изменения (эволюции) оскулирующих элементов спутниковой орбиты с производными пертурбационной функции по элементам орбиты. В согласии с принципом суперпозиции пертурбационная функция представляет собой сумму потенциалов возмущающих движение ИСЗ сил, векторная сумма которых равна возмущающей силе 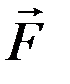. Иными словами,

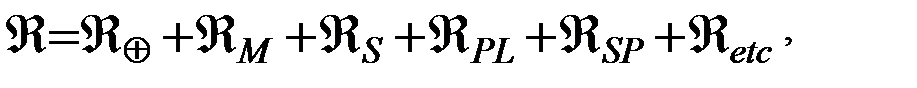(5.3.5)

где 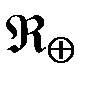- пертурбационная функция возмущающей составляющей притяжения Земли (включая влияние полярного сжатия земного эллипсоида),

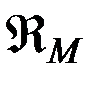- пертурбационная функция притяжения Луны,

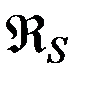- пертурбационная функция притяжения Солнца,

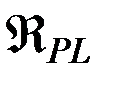- пертурбационная функция притяжения планет,

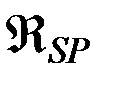- пертурбационная функция сил светового давления,

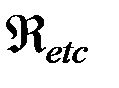- пертурбационная функция прочих возмущающих сил.

Заметим попутно, что сила сопротивления атмосферы не имеет потенциала и потому не входит в пертурбационную функцию 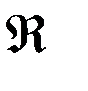. По этой причине для высоких спутников (высота над поверхностью Земли более 2000-3000 км) в качестве исходных уравнений для последующего интегрирования по времени в большинстве случаев используются уравнения Лагранжа, для более низких спутников – уравнения Ньютона.

Сказанное выше означает, что задача определения элементов оскулирующей орбиты может быть сведена к интегрированию уравнений Ньютона (5.3.3) или Лагранжа (5.3.4), однако, при этом скорости изменения элементов оскулирующей орбиты, составляющие левые части этих уравнений, не являются непосредственно наблюдаемыми величинами. Наблюдения фиксируют лишь изменения элементов на некотором интервале времени, например, на одном или нескольких витках. В частности, изменения элементов на одном витке будут, очевидно, составлять

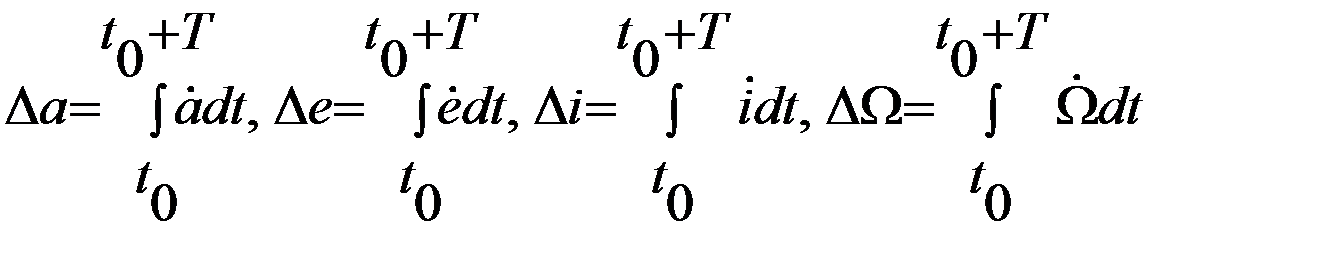и т.д.,

где T– период обращения спутника (продолжительность витка).

Поскольку правые части уравнений Лагранжа (5.3.4) от времени 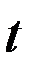явным образом не зависят, в качестве переменной интегрирования удобнее выбрать истинную аномалию 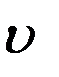– угол между направлениями на перицентр и обращающееся по эллипсу тело. Таким образом, радиус-вектор 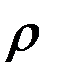и истинная аномалия 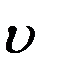выступают в роли пары полярных координат спутника в плоскости его орбиты и связаны уравнением эллипса:

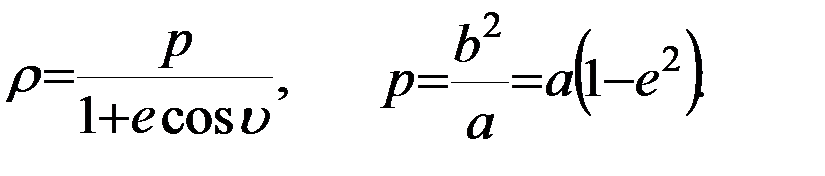
Согласно второму закону Кеплера, площадь эллиптического сектора, заключенного между радиусами-векторами любых двух положений спутника, пропорциональна времени, которое требуется для перемещения спутника из одного положения в другое. Иными словами, производная площади сектора, заключенного между двумя радиусами-векторами, по времени постоянна. 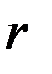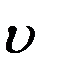Так как элемент площади сектора в полярных координатах и равен 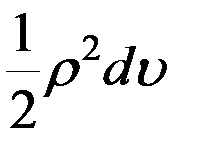, второй закон Кеплера записывается в виде известного интеграла площадей:

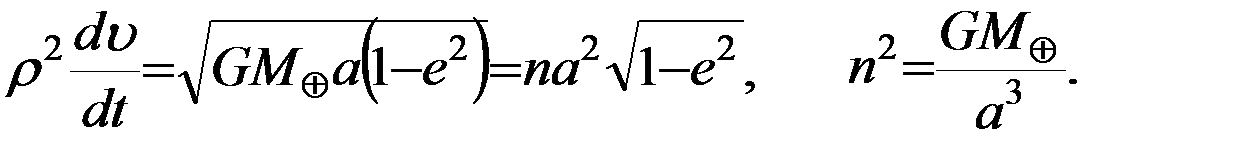
Например, для изменения долготы восходящего узла за виток с учетом (5.3.4) имеем:

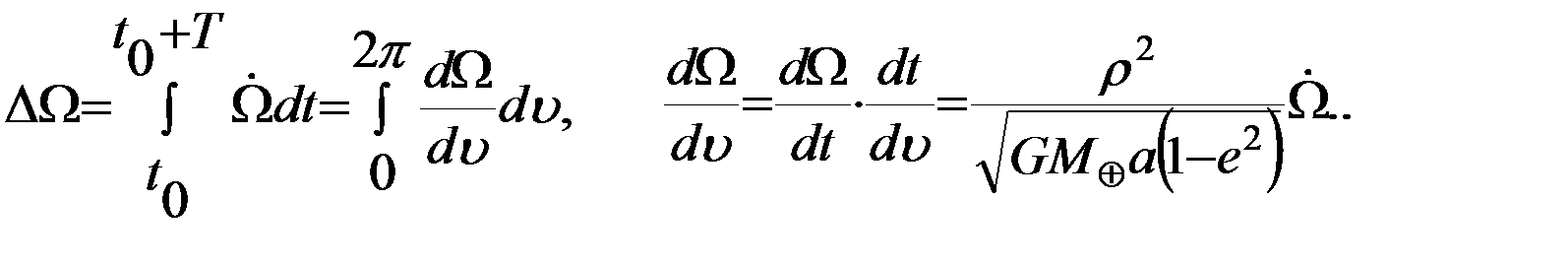
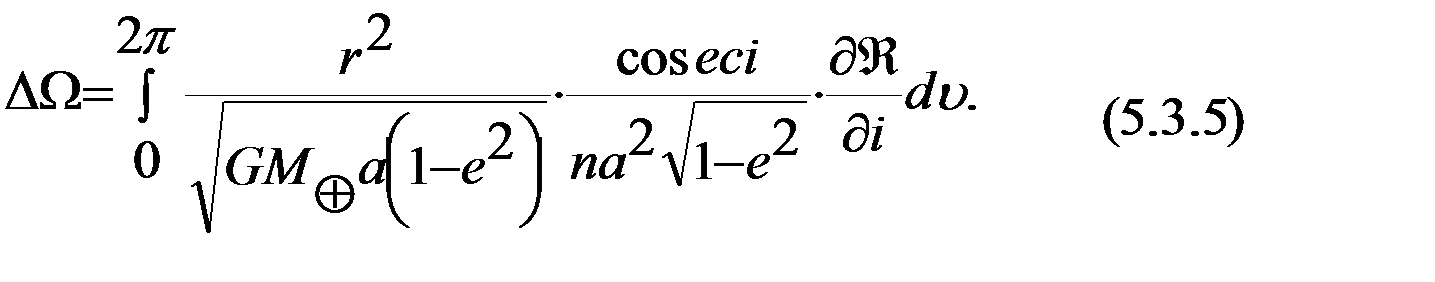
5.4. Пертурбационная функция 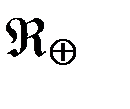возмущающего потенциала Земли

Учитывая потенциальный характер пертурбационной функции возмущающего потенциала, представим ее разложением в ряд объемных сферических (шаровых) функций:

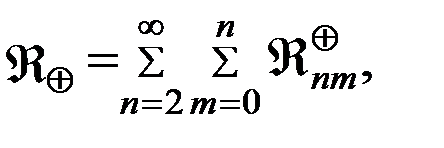где

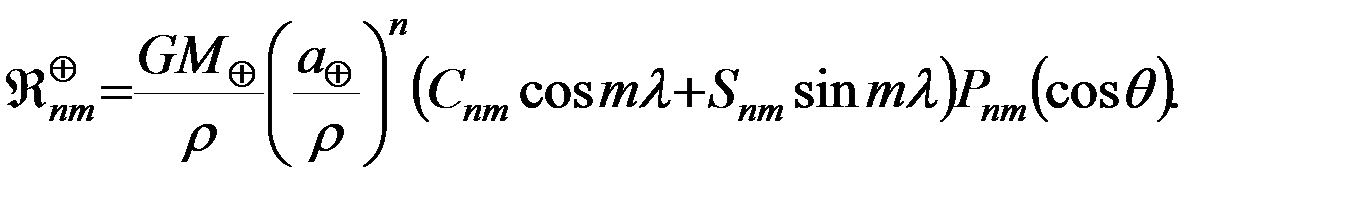(5.4.1)

Для подстановки пертурбационной функции в уравнения наблюдений вида (5.3.5) необходимо выразить ее через элементы орбиты ИСЗ. Достаточно сложные и громоздкие преобразования соотношения (5.4.1) позволяют получить пертурбационную функцию земного притяжения в следующем виде:

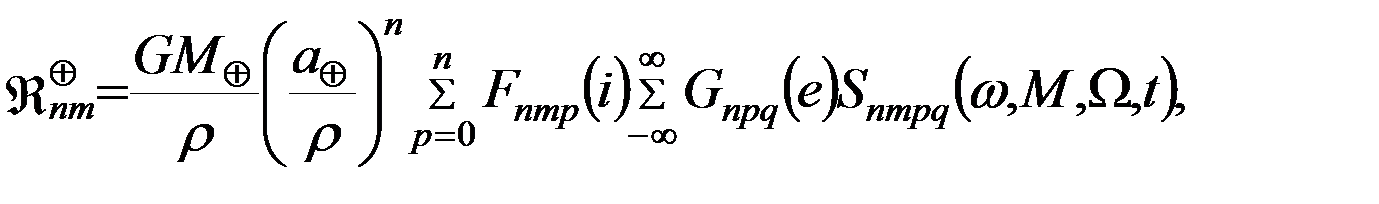(5.4.2)

в которую входят функция наклона

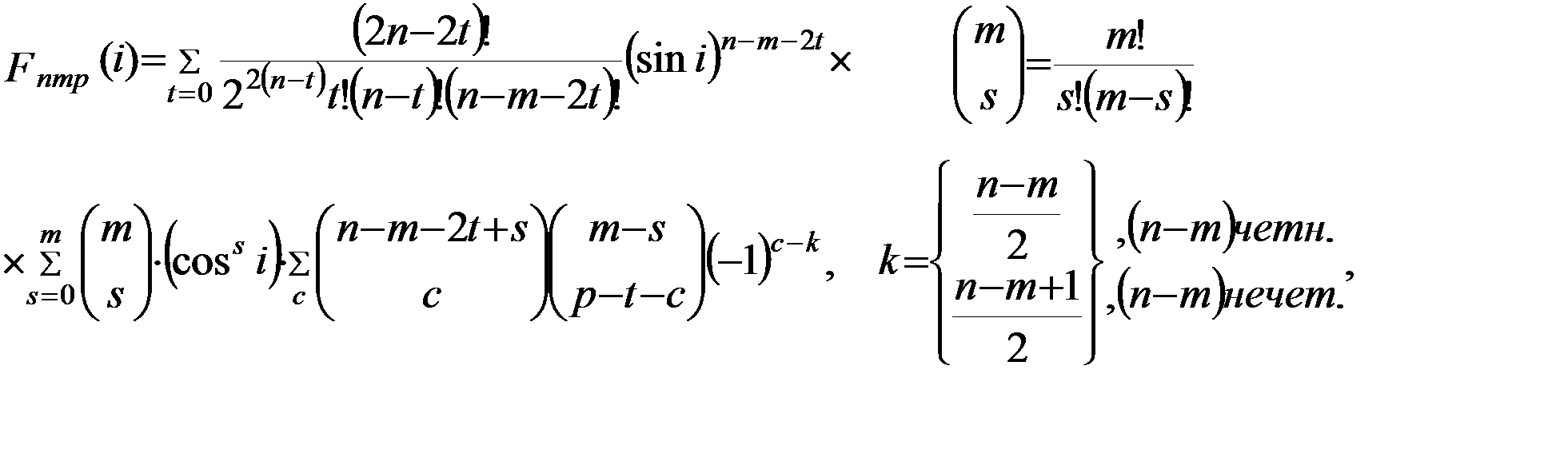зависящая от различных степеней синусов и косинусов наклонения орбиты,

а также функция эксцентриситета 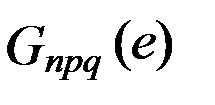, которая выражается многочленами по степеням эксцентриситета. Суммирование по индексам t и c в функции эксцентриситета выполняется для всех целых их значений, до тех пор, пока коэффициенты рядов не обращаются в ноль. Число k представляет собой целую часть отношения (n-m)/2. Наконец, функция

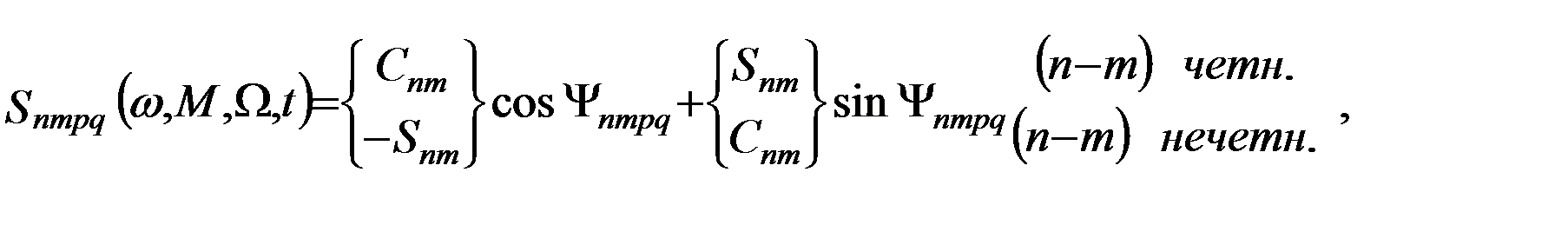
где

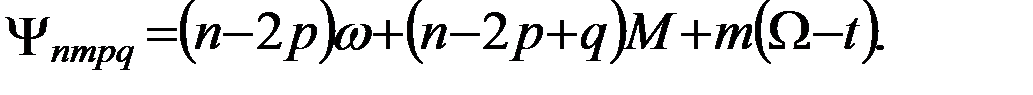(5.4.3)

Анализ приведенных здесь формул позволяет сопроводить их следующими важными комментариями.

· В формулах (5.4.2) и (5.4.3) шесть элементов орбиты представлены не зависящими друг от друга величинами, что облегчает дифференцирование пертурбационной функции возмущающего потенциала по элементам.

· Пертурбационная функция (5.4.2) с учетом (5.4.3) линейна относительно искомых гармонических коэффициентов потенциала, что позволяет использовать для оценки их значений алгоритмы метода наименьших квадратов без дополнительной линеаризации.

· Суммирование по индексу qна практике может быть ограничено интервалом (-10<q<+10),поскольку функция эксцентриситета при больших q ведет себя как функция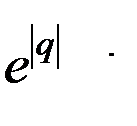

· Значения величин 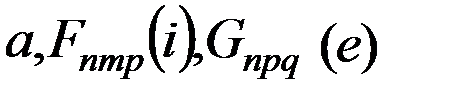, и их производных по 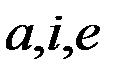при вычислении пертурбационной функции в большинстве случаев можно считать постоянными на интервале нескольких месяцев. Это означает, что все временные вариации (возмущения) элементов орбиты содержатся в функции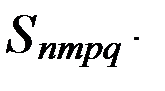

· Временные возмущения в небесной механике принято разделять на вековые, долгопериодические и короткопериодические. Вековые (непериодические) возмущения, монотонно накапливаются на значительных интервалах времени. Поскольку косинус и синус являются периодическими функциями, отсутствие периодичности в функции 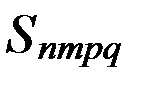означает неизменность во времени углового параметра 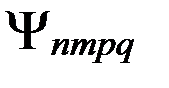. Так как величины ω, M, Ω, t зависят от времени, остается в (5.4.3) потребовать выполнения равенств: (n-2p)=0, (n-2p+q)=0, m=0, откуда имеем: n=2p, m=0, вытекающих из условия 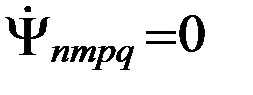. Это обстоятельство позволяет сделать важный вывод о том, что вековые изменения элементов спутниковой орбиты вызываются только влиянием зональных гармоник четной степени. Под долгопериодическими возмущениями будем понимать возмущения с периодом более суток. Иными словами, долгопериодические возмущения не должны содержать в себе гринвичского времени t, что требует в (5.4.3) выполнения условия m=0. Это означает, что долгопериодические возмущения обусловлены действием всех зональных гармоник (четных и нечетных степеней) разложения потенциала. Короткопериодические (с периодом сутки и менее) возмущения, для которых m≠0 вызываются влиянием секториальных и тессеральных гармоник.

Понятно, что в процессе наблюдений легче регистрируются вековые и долгопериодические вариации орбиты, вследствие чего значения зональных гармоник определяются увереннее и точнее. Ниже обсудим влияние зональной составляющей гравитационного потенциала на эволюцию некоторых элементов спутниковой орбиты.

Формула (5.3.5) отражает изменение долготы восходящего узла орбиты ИСЗ за один виток вследствие возмущений, описываемых пертурбационной функцией . Подстановка в выражения типа (5.3.5) пертурбационной функции геопотенциала, содержащей только зональные гармоники (m≠0), ответственные за вековые и долгопериодические возмущения спутниковой орбиты, позволяет получить формулы [ГВМ], [Груш ОснГрав]:

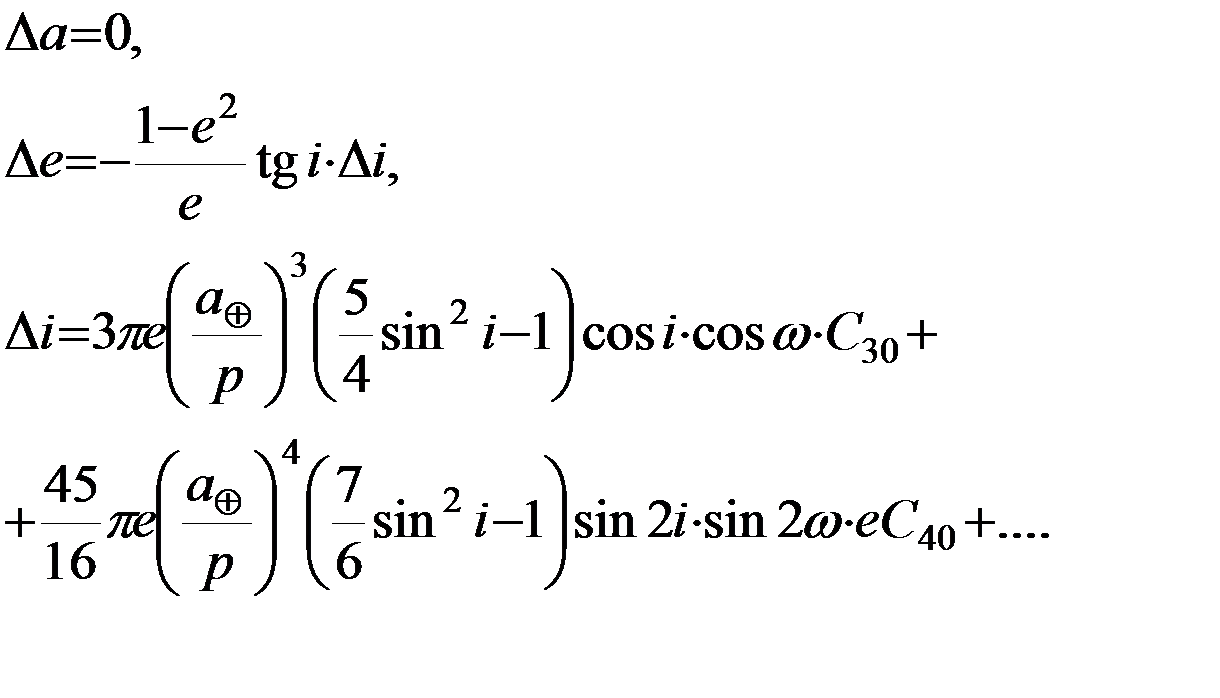
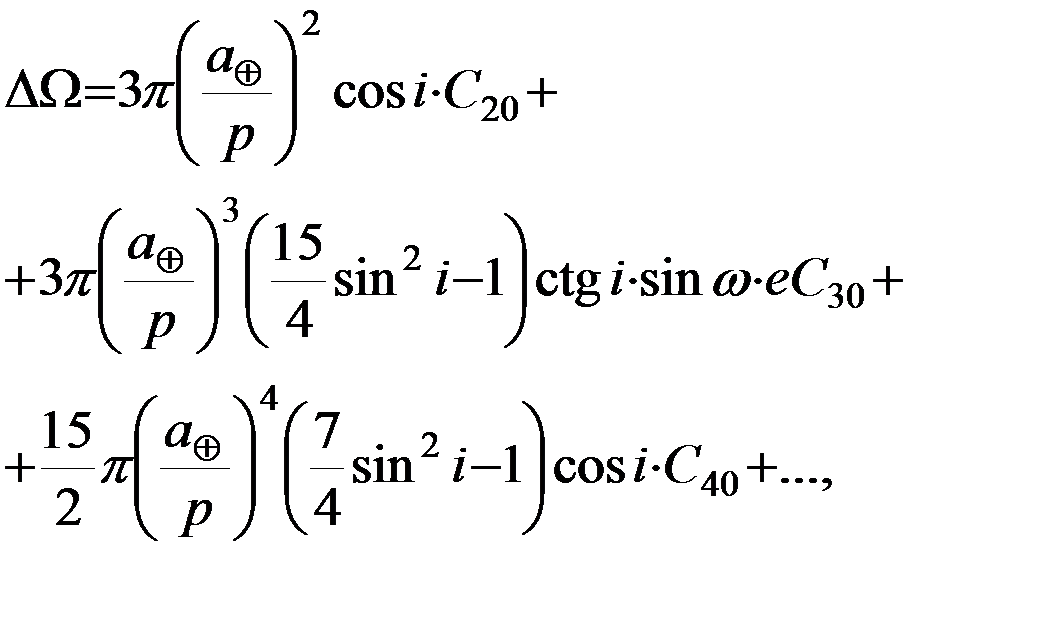(5.4.4)

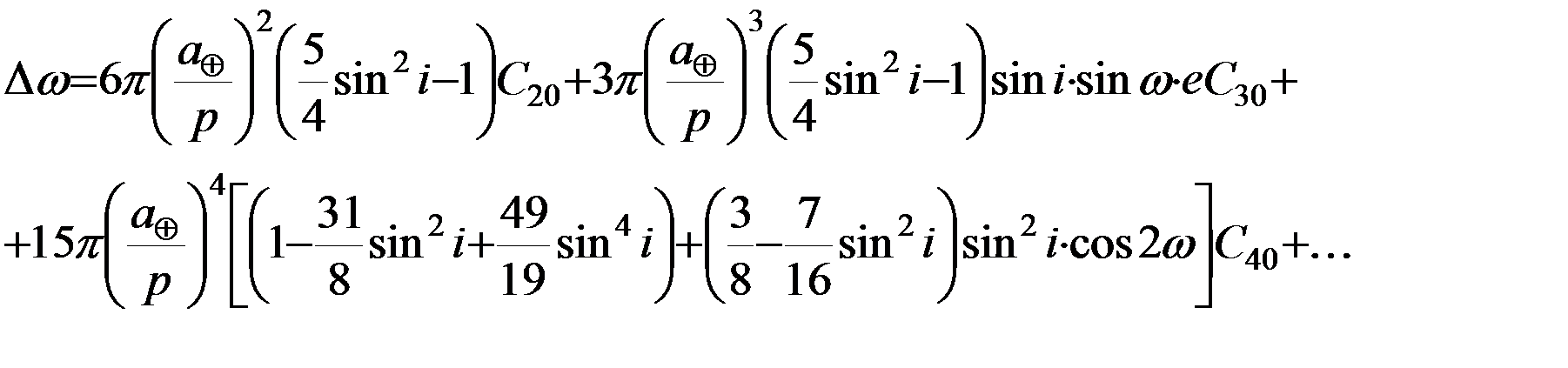
Первое уравнение системы (5.4.4) показывает что большая полуось орбиты не испытывает вековых и долгопериодических возмущений.

Второе уравнение указывает на пропорциональную зависимость возмущений эксцентриситета и наклонения. Иными словами, при наклонениях, отличных от нуля, использование возмущений эксцентриситета либо наклонения должно привести к одинаковым результатам, поскольку эти возмущения связаны с искомыми гармоническими коэффициентами одинаковым образом.

Третье уравнение для 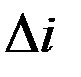содержит только долгопериодические слагаемые, определяемые сомножителями 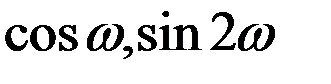и т.д., при этом первое его слагаемое, по крайней мере, на порядок эксцентриситета превышает все последующие.

Судя по четвертому и пятому уравнениям, эволюция элементов Ω и ω, претерпевающих и вековые, и долгопериодические изменения, оказывается наиболее эффективным источником информации для определения зональных гармоник разложения потенциала.

Четвертое уравнение свидетельствует о том, что описываемое зональной гармоникой второй степени 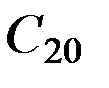сжатие фигуры Земли вдоль полярной оси вызывает вековую прецессию орбиты ИСЗ. При этом плоскость спутниковой орбиты прецессирует таким образом, что линия узлов перемещается к западу, если 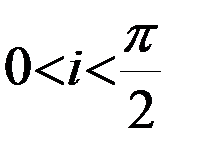, и к востоку, если 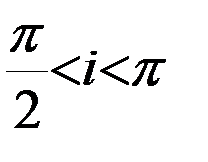. Для полярных орбит при 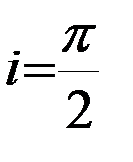долгота узла Ω не меняется вековым образом. Средняя скорость векового изменения долготы узла Ω составляет около трех градусов дуги в сутки. Также вследствие сжатия Земли происходит прецессия перигея в плоскости спутниковой орбиты. Если 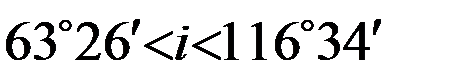, угол ω увеличивается, в остальных случаях – уменьшается со скоростью около половины градуса за сутки. Таким образом, под влиянием сжатия Земли плоскость орбиты ИСЗ прецессирует вековым образом, а сама орбита, не меняя своей формы, прецессирует в своей плоскости.

Вследствие отмеченных обстоятельств, в динамической космической геодезии для определения параметров гравитационного потенциала в качестве уравнений наблюдений используют соотношения лишь для четырех элементов: 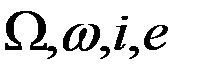[КГ]. Уравнения (5.4.4) также показывают, что величины вариаций орбитальных элементов сильно зависят от наклонения орбиты, в силу чего для получения надежной оценки значений неизвестных гармонических коэффициентов следует использовать наблюдения различных спутников с различными значениями наклонений.