Общее решение задачи оптимального различения двух сигналов
Задача формулируется следующим образом. На вход системы на заданном интервале 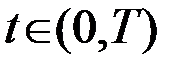 поступает наблюдение
поступает наблюдение
u(t)= 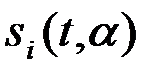 +n(t), i=1,2, aÎA ,
+n(t), i=1,2, aÎA ,  (4.2.1)
(4.2.1)
состоящее из полезного сигнала и помехи. Полезный сигнал является функцией дискретного информационного параметра i, который может принимать два значения: 1 или 2, и в общем случае векторного несущественного параметра aс множеством возможных значений A. Система по наблюдению {u(t),tÎ(0,T)}, принимает решение о том, какой сигнал из двух возможных присутствует на входе 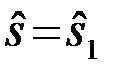 или
или  (
( 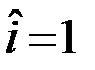 или
или 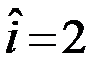 ). Заданными полагаются: детерминированные функции
). Заданными полагаются: детерминированные функции 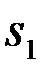 (t,a) и
(t,a) и  (t,a) времени t и параметра a, вероятности посылки первого P1 и второго P2 сигналов (P1+P2=1), плотность вероятности несущественного параметра p(a),aÎA, статистика помехи, т.е. функционал ПВ помехи. Там, где не оговаривается противное, полагается, что n(t) - основная гауссовская помеха, определенная в §3.6. Сведения известные заранее (т.е. до получения наблюдения), заданные в формулировке задачи, называются априорными (доопытными). Поэтому вероятности P1 и P2 называют априорными вероятностями сигналов
(t,a) времени t и параметра a, вероятности посылки первого P1 и второго P2 сигналов (P1+P2=1), плотность вероятности несущественного параметра p(a),aÎA, статистика помехи, т.е. функционал ПВ помехи. Там, где не оговаривается противное, полагается, что n(t) - основная гауссовская помеха, определенная в §3.6. Сведения известные заранее (т.е. до получения наблюдения), заданные в формулировке задачи, называются априорными (доопытными). Поэтому вероятности P1 и P2 называют априорными вероятностями сигналов 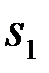 и
и 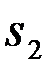 .Требуется:
.Требуется:
1). Определить оптимальный алгоритм преобразования наблюдения {u(t),tÎ(0,T)} в решение 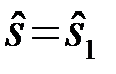 или
или  , т.е. оптимальную обработку наблюдений или оптимальную структуру РПрУ.
, т.е. оптимальную обработку наблюдений или оптимальную структуру РПрУ.
2). Дать количественную оценку качества (качественного показателя) полученной оптимальной системы. При решении задачи в общем виде мы ограничимся решением первого вопроса. Примеры решения второго вопроса будут приведены при рассмотрении конкретных задач.
Качественный показатель, по которому оптимизируются системы различения сигналов, уже был сформулирован. В нашем случае - это (4.1.4). Уточним его физический смысл. В средний риск при простой функции потерь (4.1.4) входят вероятности ошибок 2-х видов. Ошибка 1-го вида - это ошибка при передаче 1-го сигнала 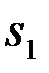 .
.
Вероятность этой ошибки Pош.1
Рош.1=Вер 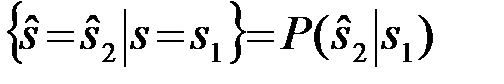 (4.2.2)
(4.2.2)
равна условной вероятности принятия решения 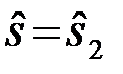 при условии, что был передан 1-ый сигнал
при условии, что был передан 1-ый сигнал 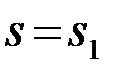 .
.
Аналогично ошибка 2-го вида - это ошибка при передаче второго сигнала 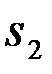 . Ее вероятность Pош.2 равна условной вероятности принятия решения
. Ее вероятность Pош.2 равна условной вероятности принятия решения 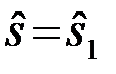 при условии, что был предан 2-ой сигнал
при условии, что был предан 2-ой сигнал 
Рош.2=Вер 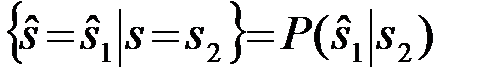 . (4.2.3)
. (4.2.3)
Средняя вероятность ошибочных решений Pошср определяется по формуле полной вероятности и равна вероятности посылки 1-го сигнала P1, умноженной на условную вероятность ошибки при посылке 1-го сигнала Pош.1, плюс вероятность посылки 2-го сигнала P2, умноженной на условную вероятность ошибки при посылке 2-го сигнала Pош.2.
Рошср= 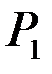 Рош.1+
Рош.1+ 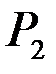 Рош.2=
Рош.2= 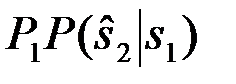 +
+ 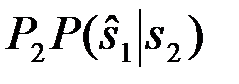 . (4.2.4)
. (4.2.4)
Таким образом, в задаче различения сигналов средний риск r при простой функции потерь равен средней вероятности ошибочных решений Pошср. При выборе функции потерь (или качественного показателя системы) принимают во внимание, что последний должен хорошо соответствовать характеру решаемой задачи и вместе с тем служить удовлетворительной основой для ее аналитического решения. Выбор не однозначен. В значительной мере ориентируются на здравый смысл.
Далее сформулируем общее правило принятия решений: 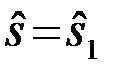 или
или  по наблюдению {u(t),tÎ(0,T)}, которое тождественно представляется вектором отсчетов
по наблюдению {u(t),tÎ(0,T)}, которое тождественно представляется вектором отсчетов 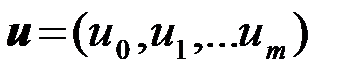 . На рис. 4.1. условно представлено множество U всех возможных значений вектора наблюдений
. На рис. 4.1. условно представлено множество U всех возможных значений вектора наблюдений 
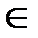 U.
U.
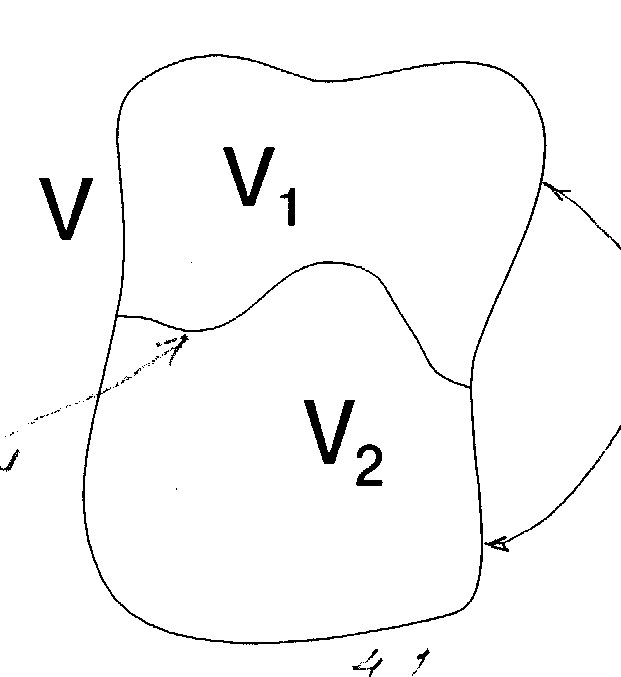
Рис. 4.1
Для того чтобы принять решение нужно каждому элементу множества U поставить в соответствие одно из двух решений 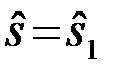 или
или  . Это значит, что нужно разделить все множество U на два подмножества U1 и U2 (рис.4.1) и принимать решения в зависимости от того, в какое из подмножеств попадает наблюдение
. Это значит, что нужно разделить все множество U на два подмножества U1 и U2 (рис.4.1) и принимать решения в зависимости от того, в какое из подмножеств попадает наблюдение  . Таким образом, общее решающее правило может быть сформулировано так:
. Таким образом, общее решающее правило может быть сформулировано так:
если  ÎU1, принимается решение
ÎU1, принимается решение 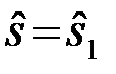
(4.2.5)
если  ÎU2, принимается решение
ÎU2, принимается решение 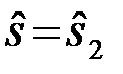
Задача определения оптимального правила решений при различении двух сигналов теперь сводится к оптимальному разделению множества U на два подмножества U1 и U2.
Найдем выражение для вероятностей ошибок Pош.1,Pош.2 и Рошср с учетом правила решений (5). Учтем также, что сведения, заданные условиями задачи, определяют условные ПВ 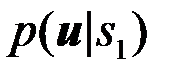 и
и 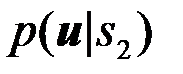 наблюдения
наблюдения  при условии, что послан сигнал
при условии, что послан сигнал 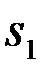 и
и 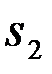 . Вероятность попадания
. Вероятность попадания  в область U2 (решение
в область U2 (решение 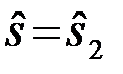 ) при условии посылки сигнала
) при условии посылки сигнала 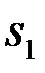 равна интегралу ПВ
равна интегралу ПВ  по области
по области  ÎU2. Соответственно
ÎU2. Соответственно
Pош.1=Вер{  Î
Î 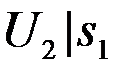 }=
}= 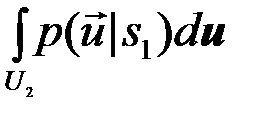 . (4.2.6)
. (4.2.6)
В (6) используется сокращенная запись многомерного интеграла по области U2, причем 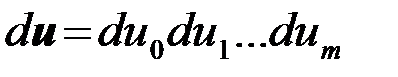 . Аналогично
. Аналогично
Pош.2=Вер{  ÎU1|s2}=
ÎU1|s2}= 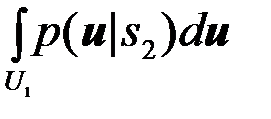 . (4.2.7)
. (4.2.7)
и (4) принимает вид
Рошср= 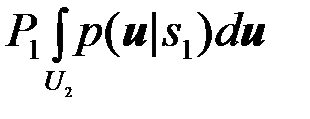 +
+  . (4.2.8)
. (4.2.8)
К правой части (8) прибавим и вычтем слагаемое
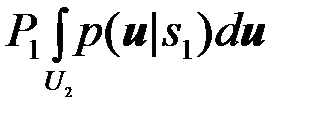 .
.
Тогда, учитывая, что
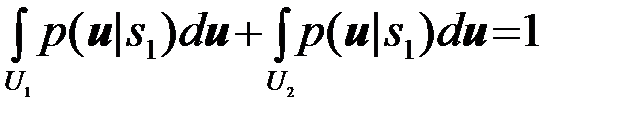 ,
,
получаем
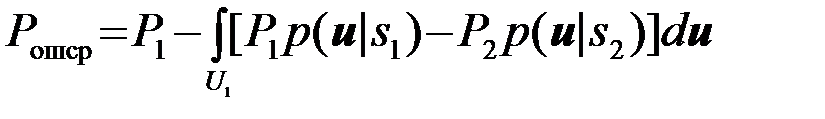 . (4.2.9)
. (4.2.9)
Согласно выбранному критерию оптимальным является такое правило принятия решений, которое минимизирует Рошср и, следовательно, максимизирует интеграл в (9). Задача определения оптимального правила принятия решений сводится теперь к выбору области U1 из условия:
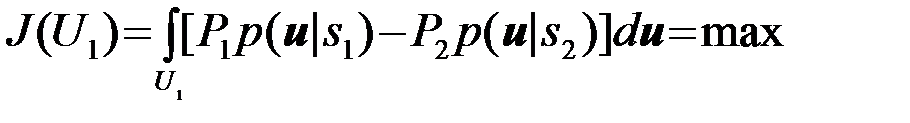 . (4.2.10)
. (4.2.10)
Максимизация интеграла J(U1) обеспечивается, если к области U1 отнести все те значения наблюдения  , при которых подынтегральное выражение в (10) положительно, т.е. нужно принять
, при которых подынтегральное выражение в (10) положительно, т.е. нужно принять
 , если
, если 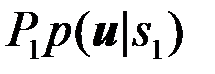

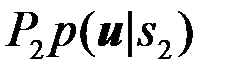 . (4.2.11)
. (4.2.11)
Точки пространства U, для которых справедливо противоположное неравенство должны быть отнесены к области U2
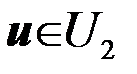 , если
, если 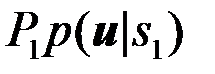

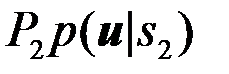 . (4.2.12)
. (4.2.12)
Tочки пространства, соответствующие нулю подынтегрального выражения (10)
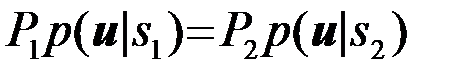 (4.2.13)
(4.2.13)
определяют границу между оптимальными областями U1 и U2 (граничную поверхность). Если наблюдение 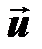 таково, что удовлетворяется равенство (13), то безразлично какое из двух решений будет принято
таково, что удовлетворяется равенство (13), то безразлично какое из двух решений будет принято 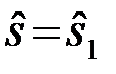 или
или 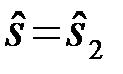 , величина Рошср при этом не меняется.
, величина Рошср при этом не меняется.
Таким образом, оптимальный по критерию Рошср=min, алгоритм принятия решений состоит в следующем:
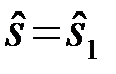 (
(  ), если
), если 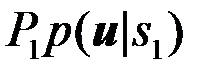

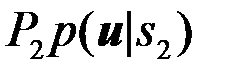
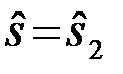 (
( 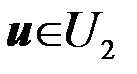 ), если
), если 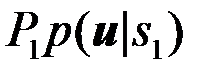

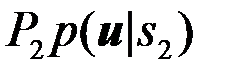
и кратко записывается так
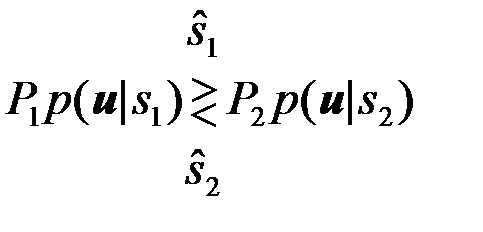 . (4.2.14)
. (4.2.14)
Оптимальная система должна по принятому наблюдению  сформировать функции правдоподобия
сформировать функции правдоподобия 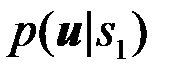 сигнала
сигнала 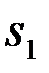 и
и 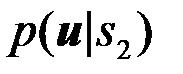 сигнала
сигнала 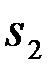 (условные ПВ принятого наблюдения), умножить их на вероятности P1 и P2 соответственно. Полученные произведения сравниваются между собой. Решение
(условные ПВ принятого наблюдения), умножить их на вероятности P1 и P2 соответственно. Полученные произведения сравниваются между собой. Решение 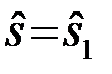 принимается, если больше
принимается, если больше 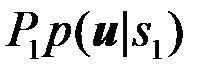 и наоборот.
и наоборот.
Приведенное общее решение задачи оптимального различения двух сигналов мы конкретизируем для нескольких частных случаев, представляющих практический интерес. Предварительно представим в несколько преобразованном виде оптимальное правило решений (14). Для этого определим условные вероятности 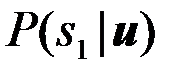 и
и 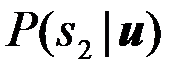 первого
первого 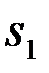 и второго
и второго 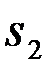 сигналов при условии, что принято данное конкретное наблюдение
сигналов при условии, что принято данное конкретное наблюдение  . Эти вероятности называются апостериорными (послеопытными) вероятностями сигналов
. Эти вероятности называются апостериорными (послеопытными) вероятностями сигналов 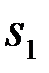 и
и  . Если ПВ вектора наблюдений
. Если ПВ вектора наблюдений  обозначить
обозначить 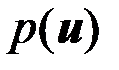 , то согласно формуле обратной вероятности Байеса
, то согласно формуле обратной вероятности Байеса
 ,
, 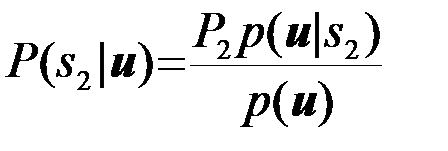 . (4.2.15)
. (4.2.15)
Правую и левую часть неравенств, определяющих правило решений (14) разделим на одну и ту же положительную величин 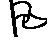
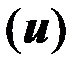 . При этом оптимальное правило решений принимает вид
. При этом оптимальное правило решений принимает вид
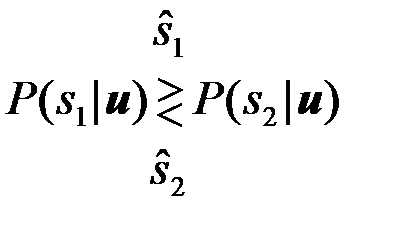 (4.2.16)
(4.2.16)
Следовательно, оптимальное (по критерию Pошср=min) различение сигналов можно свести к формированию апостериорных вероятностей для каждого сигнала (s1,s2) и к их сравнению. Решение принимается по максимуму апостериорной вероятности.
