Классификация моделей сигналов

Во 2-ой и 3-ей главах изучаются математические модели сообщений, переносчиков сообщений - сигналов, принимаемых колебаний, помех и других функций времени, с которыми приходится иметь дело в теории РТС. Кратко все эти модели будем называть моделями сигналов и обозначать символом x(t). Используются детерминированные и случайные (стохастические) модели. Детерминированные модели представляют собой обычные функции x(t), изучаемые в математическом анализе и ставящие в однозначное соответствие каждому значению аргумента t (имеющему в рассматриваемом случае смысл времени) определенное значение функции x. В отличие от детерминированных функций у случайных функций (или моделей) такое однозначное соответствие отсутствует. Случайная функция является исходом случайного эксперимента и непредсказуемым образом принимает вид конкретной функции x(t,w)из некоторого множества функций {x(t,w), wÎW}, где Wмножество исходов случайного эксперимента. Существенно, что в множестве W должна быть определена вероятностная мера - вероятность попадания исхода wв любое подмножество множества W. В статистической теории РТС сообщения и сигналы, содержащие сообщения, стараются представить случайными моделями, исходя из того, что сообщения в процессе работы источника непредсказуемым образом принимают вид конкретных функций l(t,w) из совокупности возможных реализаций{l(t,w),wÎW}.Если бы можно было предсказать достоверно, какой конкретно вид примет сообщение l(t,w), то необходимость в его передаче отпала бы. Однако далеко не всегда в пространстве исходов wÎW удается ввести вероятностную меру. Кроме того, конкретные реализации передаваемых сообщений l(t,w) или в общем случае конкретные реализации случайных сигналов х(t,w) являются детерминированными функциями х(t). Поэтому представляют интерес как случайные модели сигналов, так и детерминированные. В настоящей главе рассматриваются детерминированные модели сигналов, а в следующей - случайные.

Для каждого сигнала или для его модели x(t) должны быть заданы область определения tÎT, где T - ограниченный или неограниченный временной интервал и множество X возможных значений сигнала xÎX. В зависимости от структуры множеств T и X различают следующие виды сигналов и их моделей:

a) Непрерывный или аналоговый сигнал. Множество T возможных значений переменной t, а также множество X возможных значений сигнала x непрерывное, т.е. представляет собой множество точек конечного или бесконечного отрезка, называемое континуумом (континуальным множеством).

b) Дискретный сигнал. Множество T определения сигнала дискретное, конечное 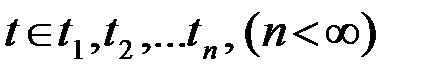или бесконечное, счетное 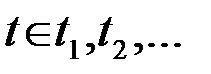. Множество X значений сигнала континуальное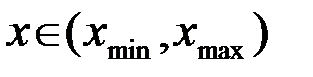

c) Цифровой сигнал. Множество T значений t и множество X значений x дискретные.

Реальные сигналы являются вещественными функциями. Однако используются и комплексные (аналитические) модели вещественных сигналов. При рассмотрении сигналов и их моделей там, где не оговаривается противное, имеются в виду вещественные функции. Приводимая теория сигналов является далеко не полной. В ней отражены только те закономерности и соотношения, которые будут использованы при изложении основного материала.