Определение временных характеристик типовых

ЗВЕНЬЕВ И СИСТЕМЫ автоматического управления

Цель работы

Целью работы является изучение временных характеристик типовых динамических звеньев и методов их графического построения по заданным передаточным функциям.

Теоретическая часть

Динамические свойства линейных звеньев и систем автоматического управления могут быть описаны как дифференциальными уравнениями, так и графическими характеристиками. Процесс нахождения дифференциального уравнения системы через уравнения ее элементов в общем случае является довольно трудоемким. Исследование САУ существенно упрощается при использовании прикладных математических методов операционного исчисления в частности преобразований Лапласа. Преобразование дифференциальных уравнений по Лапласу является основой чрезвычайно удобного для исследований САУ метода передаточных функций. С помощью передаточных функций можно легко оценить динамические свойства любого элемента САУ.

2.1. Передаточной функцией W(s) звена (системы) называется отношение преобразования по Лапласу выходной координаты X(s) звена (системы) к изображению по Лапласу входной координаты Y(s) при нулевых начальных условиях:

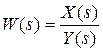. (1)

Под временными характеристиками динамического звена (системы) в общем случае понимается графическое изображение процесса изменения выходной величины в функции времени при переходе звена из одного равновесного состояния в другое. Так как дифференциальное уравнение тоже определяет изменение выходной величины в функции времени при некоторых начальных условиях, то временная характеристика представляет собой графическую форму решения дифференциального уравнения звена для принятого типового воздействия и, следовательно, полностью характеризует динамические свойства звена (системы).

2.2. Временные характеристики могут быть получены не только путем решения дифференциального уравнения системы, но и экспериментальным путем. Это имеет исключительно важное практическое значение, поскольку в этом случае не требуется выводить и решать дифференциальное уравнение, что является в общем случае очень трудоемкой, а иногда и неразрешимой задачей. Временные характеристики прежде всего зависят от внешнего воздействия (входного воздействия y(t) или возмущения f(t)). Обычно в линейных звеньях при определении временных характеристик по какому-либо одному из внешних воздействий все другие внешние воздействия полагаются равными нулю. Законы изменения внешних воздействий заранее, как правило, неизвестны, т.е. представляют собой случайные функции времени. Поэтому для исследования САУ используются так называемые типовые законы изменения внешних воздействий. Каждому такому типовому закону соответствует своя временная характеристика (функция). Рассмотрим основные типовые воздействия и соответствующие им переходные (временные характеристики).

2.2.1.Переходная функция, илипереходная характеристика, h(t) описывает переходной процесс на выходе звена (системы), возникающий при подаче на его вход скачкообразного воздействия, которое мгновенно возрастает от нуля до единицы и далее остается неизменным при нулевых начальных условиях.

2.2.2. Единичная ступенчатая функция 1(t).Типовое входное воздействие, при котором функция y(t)=1(t) определяется соотношениями y(t) =0 при t < 0 и y(t) =1 при t³ 0, т.е.

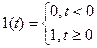(2)

называется единичной ступенчатой функцией 1(t) – рисунок 1а. Предполагается, что единичной ступенчатой функцией 1(t) имеет туже размерность, что и физическая величина на входе звена. Если воздействие представляет собой неединичную ступенчатую функцию y(t)=у_уст.×1(t), выходная величина будет равна x(t)= у_уст.h(t).

Ступенчатая функция представляет собой распространенный вид входного воздействия в САУ. К такому виду сводятся мгновенное изменение нагрузки электрического генератора, мгновенное возрастание нагрузки на валу двигателя, мгновенный поворот командной оси следящей системы и т.п. Умножение какой-либо функции времени x(t) на единичную ступенчатую функцию 1(t) означает, что функция времени x(t) будет существовать только при t³ 0, при t < 0 она обращается в нуль.

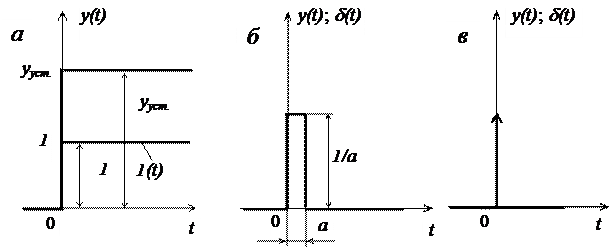Рисунок 1 – Типовые входные воздействия

а – ступенчатые функции – единичная и произвольной величины;

б - единичная импульсная функция конечных параметров;

в - единичная импульсная функция нулевой ширины

2.2.3. Импульсная переходная функцияили весовая функция (функция веса) - w(t)описывает переходной процесс на выходе звена (реакцию звена, системы), возникающий при подаче на его вход единичного импульса при нулевых начальных условиях.

2.2.4. Единичный импульс – дельта-функция d(t)– это математическая идеализация предельно короткого импульсного сигнала, площадь которого равна единице при длительности равной нулю, и высоте равной бесконечности. Дельта-функция представляет собой производную от единичной ступенчатой функции

d(t) = 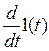= 1¢(t) (3)

или в операционной форме

d(s) = sL[1(t)] = s 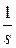=1. (4)

Поэтому

L[w(t)] = W(s) d(s) =W(s),(5)

т.е. изображение импульсной переходной функции равно передаточной функции. Отсюда, для характеристики динамических свойств звена (системы) в равной мере могут быть использованы как передаточная, так и импульсная переходная функция. Дельта-функция тождественно равна нулю повсюду, кроме точки t = 0, где она стремится к бесконечности. Основное свойство дельта-функции заключается в том, что

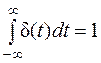. (6)

Формула (6) означает, что площадь под дельта-функцией равна единице. Из (6) также следует, что ее размерность равна [с^-1]. Функции W(s), h(t) и w(t) связаны между собой:

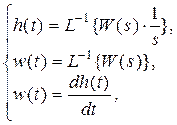(8)

где L^-1{×} – обратное преобразование Лапласа; 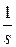– изображение по Лапласу функции 1(t).

Импульсная функция также представляет собой распространенный вид входного воздействия в автоматических системах. Это, например, кратковременный удар нагрузки на валу двигателя, кратковременный ток короткого замыкания генератора, отключаемого плавкими предохранителями и т.д.

При практических расчетах наиболее широкое применение находит временная характеристика в виде переходной характеристики, так как ее достаточно просто получить экспериментально и, кроме того, определяемый ею переходный процесс в системе часто возникает при включениях и изменении задания регулятору.

Для определения временных характеристик единичное скачкообразное постоянное или в виде импульса воздействие принято для того, чтобы однозначно оценивать динамические свойства звена или системы, так как при различной величине воздействий выходная величина даже одной и той же системы будет изменяться по-разному. Кроме того, использование ступенчатого постоянного или импульсного воздействия в виде стандартного входного сигнала имеет также и то преимущество, что действительные, любой формы, возмущающие воздействия на систему можно представить в виде последовательности таких сигналов, например так как показано на рисунке 2.

Рисунок 2 – Представление входного воздействия произвольной формы суммой входных ступенчатых воздействий

При поступлении на вход звена или разомкнутой системы с передаточной функцией W(p) входной величины y(t) = 1(t) на выходе получаем переходную характеристику x = h(t). Входная и выходная величины, преобразованные по Лапласу запишутся следующим образом

Y(p) = L[y(t)] = L[1(t)] = 1/p; (9)

X(p) = L[h(t)] = h(p). (10)

С учетом этих соотношений получим:

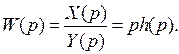(11)

Из выражения (11) следует, что по временной характеристике системы (по переходной функции) можно получить передаточную функцию системы. В свою очередь изображение по Лапласу переходной функции определяется выражением

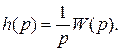(12)

Из выражения (12) с помощью обратного преобразования Лапласа можно определить переходную функцию разомкнутой системы:

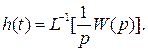(13)

Аналогично переходная функция замкнутой системы имеет вид:

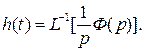(14)

2.3. Апериодическое звено - инерционное звено первого порядка.Звену соответствует дифференциальное уравнение

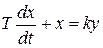. (15)

В операторной форме уравнение имеет вид:

TpX(p) + X(p) = kY(p). (16)

Передаточная функция звена

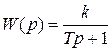. (17)

Определим характер изменения выходной величины X(p) при изменении скачком входной величины y(t) = y_уст.×1(t) (где y_уст. – величина скачка). По таблицам преобразований Лапласа изображение входной величины имеет вид:

Y(p)= L[y(t)] = L[y_уст.×1(t)] = y_уст./p.(18)

По формуле (1) можно определить изображение выходной величины

X(p) = W(p)Y(p). (19)

Тогда с учетом (17) и (18) из (19) получим:

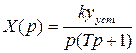(20)

Оригинал функции x(t) через ее изображение находится по таблице преобразований Лапласа после того, как в формуле (20) вынести постоянные величины за знак преобразования Лапласа

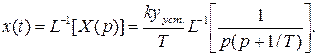(21)

Полагая, что 1/T = а, по таблице преобразований Лапласа можно найти

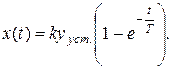(22)

Апериодическими звеньями первого порядка является, например, резервуар с газом, у которого входная величина представляет собой давление p₁ впускным отверстием, а выходная – давление p₂ в резервуаре – рисунок 3а.

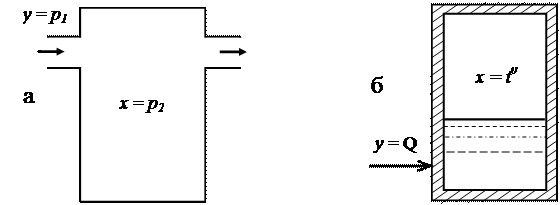
Рисунок 3 – Примеры устройств, работа которых описывается

апериодическими звеньями первого порядка

а – резервуар с газом; б – нагревательная печь

Другим примером может служить нагревательная печь - рисунок 3б, у которой входная величина – количество поступающего в единицу времени тепла Q, а выходная - температура в печи t⁰.

2.3.1. Переходная функция h(t) апериодического звена получается из уравнения (22) при y_уст. = 1 – при подаче на вход звена единичного ступенчатого воздействия 1(t)

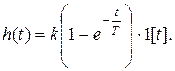(23)

Переходной процесс апериодического звена (22) представлен на рисунке 4.

Графические зависимости переходного процесса имеют вид экспонент. Поэтому время t, необходимое для того, чтобы выходная величина x(t) достигла установившегося значения x(t) = x_уст. = ky_уст. (при единичном входном сигнале y_уст. = 1, а x(t)= x_уст. = k), теоретически бесконечно велико. Величина T имеет размерность времени и называется постоянной времени. Физический смысл постоянной времени заключается в том, что это время, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости изменения ее в начальный момент времени.

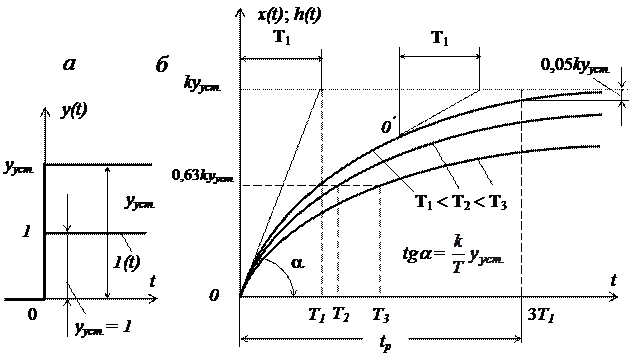
Рисунок 4 - Переходной процесс - переходная функция апериодического звена

а – графики скачкообразного изменения входной величины у апериодического звена (единичного и произвольной величины); б – графики переходной функции апериодического звена - изменения выходной величины при различных значениях постоянной времени

Постоянная времени определяет динамические свойства звена. Чем она больше, тем медленнее протекает переходный процесс в звене, и наоборот. В частности, при T = 0 процесс протекает в звене мгновенно и инерционное звено превращается в безынерционное усилительное звено. При t = T значение выходной величины составляет 63% нового установившегося значения. Постоянная времени апериодического звена геометрически определяется как проекция на ось времени отрезка касательной к экспоненте, заключенного между точкой касания и точкой пересечения касательной с линией установившегося значения выходной величины. Длина этой проекции одинакова для касательных, проведенных в любой точке экспоненты (точки 0 и 0¢). Практически переходной процесс считается закончившимся через промежуток времени t_р = 3T.

2.3.2. Импульсная переходная функция w(t) апериодического звена - реакция апериодического звенана импульсное входное воздействие может быть найдена дифференцированием переходной функции h(t).

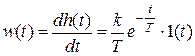. (24)

Вид импульсной переходной функции звенапоказан на рисунке 5.

2.4. Безынерционное (пропорциональное, усилительное) звено.Это звено не только в статике, но и в динамике описывается алгебраическим уравнением

x(t) = ky(t). (25)

Передаточная функция звена равна постоянной величине

W(p) = k. (26)

Примером такого звена является механический редуктор (без учета явлений скручивания и люфта), усилитель, делитель напряжения и т.п. Безынерционное звено является некоторой идеализацией реальных звеньев. В действительности ни одно звено не имеет постоянную времени равную нулю. К такому звену сводится одно из реальных звеньев, например, апериодическое, колебательное и др. если можно пренебречь влиянием динамических (переходных) процессов в этом звене (при T =0).

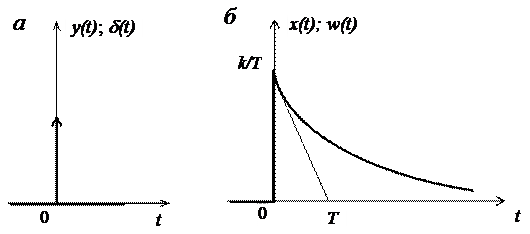Рисунок 5 - Импульсная переходная функция апериодического звена

a – импульсное воздействие d(t) на входе апериодического звена;

б – график импульсной переходной функции апериодического звена

2.4.1. Переходная функция такого звена представляет собой ступенчатую функцию, т.е. при

y(t) = 1(t); (27)

x(t) = h(t) = k×1(t). (28)

Выражение (28) для переходной функции усилительного звена получается из (23) апериодического звена при T = 0, когда инерционное звено превращается в безынерционное. Переходный процесс усилительного звена показан на рисунке 6.

2.4.2. Импульсная переходная функция (функция веса) усилительного звена представляет собой функцию, площадь которой равна k, т.е. при

y(t) = d(t); (29)

x(t) = w(t) = k×d(t). (30)

Из (30) видно, что график импульсной переходной функции усилительного звена совпадает с графиком дельта-функция d(t) - рисунок 1в.

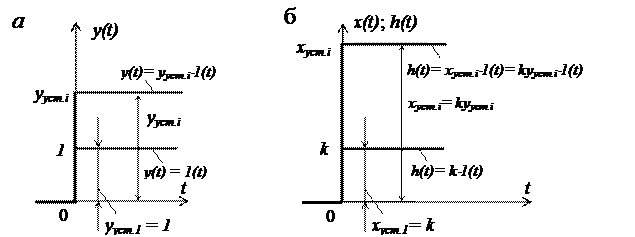Рисунок 6 – Переходный процесс усилительного звена

а – графики скачкообразного изменения входной величины усилительного звена (единичного и произвольной величины);

б – графики переходной функции усилительного звена

2.5. Идеальное интегрирующее звено.Выходная величина звена является интегралом по времени от величины на его входе

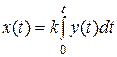. (31)

Соответственно дифференциальное уравнение интегрирующего звена

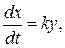(32)

где k- коэффициент усиления или передачи звена по скорости. Численно равен скорости изменения выходной величины при единичном значении входной величины.

Уравнение звена в операционной форме

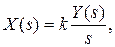(33)

откуда передаточная функция звена

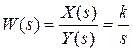. (34)

Если ко входу звена приложить воздействие в виде ступенчатой функции, то уравнение (31) примет вид:

x(t) = kyt, (35)

а переходная функция звена будет определять с помощью выражения

h(t) = kt×1(t). (36)

Импульсная переходная функция равна:

w(t) =k×1(t). (37)

Графики переходной и импульсной переходной функции интегрирующего звена приведены на рисунке 6.

б

t

t

а

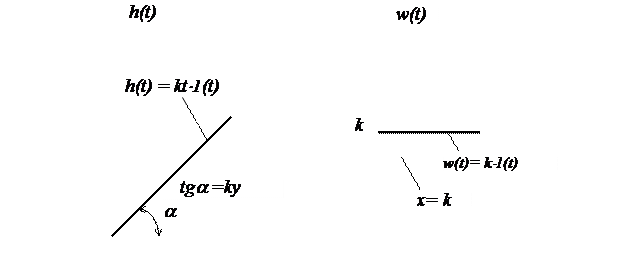
Рисунок 6 – Графики переходных процессов интегрирующего звена

а - переходная функция; б - импульсная переходная функции

Примером интегрирующего звена может служить гидравлический демпфер. Входной величиной здесь является сила F, действующая на поршень, а выходной м- перемещение поршня x. Так как скорость движения поршня пропорциональна приложенной силе (без учета инерционных сил), то

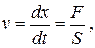
(где S – коэффициент скоростного сопротивления) его перемещение будет пропорциональным интегралу от приложенной силы

.

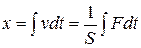Порядок выполнения работы

1.К выполнению лабораторной работы рекомендуется приступать только после внимательного ознакомления с теоретическим разделом настоящих методических указаний.

2. Письменно ответить на контрольные вопросы к лабораторной работе. Отчет с ответами утвердить у преподавателя.

3. В исследуемой следящей системе (рис.1) по передаточным функциям элементов определить тип каждого динамического звена рассчитать и построить для электромашинного усилителя, исполнительного двигателя с редуктором и корректирующего устройства следующие характеристики:

- переходную h(t);

- весовую w(t);

4. Оформить выполненную работу в виде отчета в соответствии с требованиями ГОСТа 2.105-95. Отчет выполнять на листах формата А4 (210х297 мм). Листы должны иметь штамп для текстовых документов (форма 2а, ГОСT 2.104-68).

5. Защитить выполненную работу у преподавателя и сдать отчет.

6. Все приведенные выше разделы лабораторной работы выполняются непосредственно в отведенное на лабораторную работу время (4 учебных часа).

Примечание. Исходные данные по корректирующему устройству взять из табл.2.

Требования к содержанию отчета

Отчет по лабораторной работе должен содержать:

7. Ответы на контрольные вопросы к лабораторной работе.

8. Для каждого из трех, указанных в п.3.2, звеньев, расчет, аналитические выражения и графики для h(t), w(t).

Контрольные вопросы

1. Что такое передаточная функция? Дать определение.

2. Свойства передаточной функции.

3. Как из дифференциального уравнения звена получить передаточную функцию?

4. Как по передаточной функции звена или системы составить дифференциальное уравнение?

5. Какие вы знаете типовые динамические звенья? Их передаточные функции и дифференциальные уравнения?

6. Нарисовать типовые входные воздействия.

7. Свойства дельта-функции.

8. Что такое переходная функция? Дать определение.

9. Что такое импульсная переходная функция? Дать определение.

10. Уравнения связи между W(s), h(t) и w(t).

11. Привести примеры апериодических звеньев.

12. Временные характеристики апериодического звена.

13. Безынерционное (пропорциональное, усилительное) звено. Привести примеры.

14. Временные характеристики безынерционного звена.

15. Привести примеры идеальных интегрирующих звеньев.

16. Временные характеристики идеального интегрирующего звена.

Литература

1 Востриков А.С. Теория автоматического регулирования: Учеб. пособие для вузов /А.С. Востриков, Г.А. Французова. – М.: Высшая школа. 2004.

2 Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. Учебное пособие для вузов. СПб: Профессия, 2003. 2004.

3 Филлипс Ч., Харбор Р. Системы управления с обратной связью. – М.: Лаборатория Базовых Знаний, 2001.

4 Дорф Р., Бишоп Р. Современные системы управления. – М.: Лаб. Базовых Знаний, 2002.

5 Анализ устойчивости систем автоматического управления: учебное пособие /под ред. Б.Г.Ильясова; Уфимск. гос. авиац. техн. ун-т. – Уфа: УГАТУ, 2006. – 204 с.

6 Дунин С.Е., Золотов Н.С. Теория автоматического управления. – М.: Высшая школа, 2003.