Из всех прямоугольников с периметром 16 см найти тот, который имеет наибольшую площадь.
15. Вторая производная, её физический смысл
Пусть функция  дифференцируема в некотором интервале
дифференцируема в некотором интервале 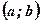 . Продифференцировав ее по аргументу х, мы получаем первую производную
. Продифференцировав ее по аргументу х, мы получаем первую производную  от функции
от функции  .
.
 - первая производная от функции
- первая производная от функции  или производная первого порядка от функции
или производная первого порядка от функции  .
.
Определение: Производная от производной первого порядка от данной функции называется производной второго порядка от этой функции.

Пример: Вычислить вторую производную функции 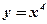 .
.
Решение:
 ;
;  .
.
Упражнения: Найти производную 2-ого порядка для функций:
1)  ; ; | 2) 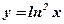 ; ; | 3)  ; ; | 4)  ; ; | 5)  . . |
Вывод: Вторая производная функции в точке – ускорение изменения функции в этой точке.
16. Выпуклость, точки перегиба графика функции
Графики функций имеют различное положение по отношению к оси абсцисс Ох. Поэтому вводится понятие выпуклости графика функции.
Определение: График функции называется выпуклым вверх на данном отрезке, если все точки графика лежат выше (не ниже) хорды, соединяющей любые две его точки. Рис. 1.
Определение: График функции называется выпуклым вниз на данном отрезке, если все точки графика лежат ниже (не выше) хорды, соединяющей любые две его точки. Рис. 2.
Определение: Точка перехода графика функции от выпуклости вверх к выпуклости вниз и наоборот называется точкой перегиба графика функции. Рис. 3.

Для определения выпуклости вверх и выпуклости вниз графика функции существует теорема.
 Теорема: Если вторая производная функции
Теорема: Если вторая производная функции  на отрезке
на отрезке 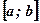 отрицательна, то график функции на этом отрезке выпуклый вверх, а если вторая производная функции
отрицательна, то график функции на этом отрезке выпуклый вверх, а если вторая производная функции  на отрезке
на отрезке 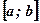 положительна, то график функции на этом отрезке выпуклый вниз.
положительна, то график функции на этом отрезке выпуклый вниз.
«Правило дождя» для запоминания теоремы о выпуклости графика функции:
Пример: Найти интервалы выпуклости графика функции  .
.
1. Найдем область определения функции: 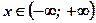 ;
;
2. Вычислим первую производную функции:  ;
;
3. Вычислим вторую производную функции:
 ;
;
4. Определим значения аргумента х, при которых вторая производная функции равна нулю:  ;
;  ;
;  ;
;  ;
;
5. Определим знак второй производной в интервалах, на которые область определения разбивается значениями аргумента  ;
;  , и характер выпуклости функции в этих интервалах:
, и характер выпуклости функции в этих интервалах:
| х |  | - 1 |  | 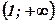 | |
 | + | - | + | ||
| у |  |  |  |
Ответ:  у – выпуклая вниз;
у – выпуклая вниз;
 у – выпуклая вверх.
у – выпуклая вверх.
Определение: Значение аргумента, при котором вторая производная функции равна нулю или не существует, называется критической точкой второго рода.
Теорема: Если непрерывная на отрезке 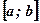 вторая производная функции в точке х0 равна нулю и при переходе аргумента через х0 меняет знак, то х0 – точка перегиба.
вторая производная функции в точке х0 равна нулю и при переходе аргумента через х0 меняет знак, то х0 – точка перегиба.
Пример: Найти точки перегиба графика функции  .
.
1. Найдем область определения функции  :
: 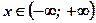 .
.
2. Вычислим производную функции:  .
.
3. Вычислим вторую производную функции:  .
.
4. Найдем критические точки второго рода функции, то есть значения аргумента х, при которых вторая производная функции равна нулю:
 ;
;  ;
;  .
.
5. Определим знак второй производной слева и справа от критической точки  , и характер выпуклости графика функции в полученных интервалах:
, и характер выпуклости графика функции в полученных интервалах:
| х |  |  | |
 | + | - | |
| у |  | перегиб |  |
6. Определим ординату точки перегиба графика функции:
 .
.
Ответ:  у - выпуклая вниз;
у - выпуклая вниз;  у - выпуклая вверх;
у - выпуклая вверх;
 - точка перегиба графика функии.
- точка перегиба графика функии.
План исследования функции на выпуклость и существование точек перегиба
1. Найти область определения функции.
2. Вычислить первую производную функции.
3. Вычислить вторую производную функции.
4. Найти критические точки 2-ого рода функции, приравняв вторую производную функции к нулю и решив полученное уравнение.
5. Определить знак второй производной функции слева и справа от критических точек.
6. Определить характер выпуклости функции в полученных интервалах области определения функции и точки перегиба функции, если они есть.
7. Вычислить значения функции в точках перегиба.
Упражнения: Исследовать на выпуклость и существование точек перегиба функции:
1. 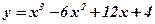 ; 2. ; 2. 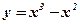 ; 3. ; 3. 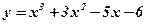 ; 4. ; 4. 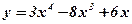 ; 5. ; 5. 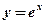 ; ; | 6. 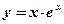 ; 7. ; 7. 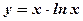 ; 8. ; 8. 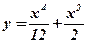 ; 9. ; 9. 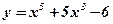 . . | 10. 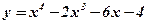 ; 11. ; 11. 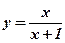 ; 12. ; 12. 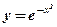 (кривая Гаусса); 13. (кривая Гаусса); 13.  . . |
17. Исследование функций и построение их графиков
Пример: Исследовать функцию  и построить ее график.
и построить ее график.
1. Найти область определения функции:  .
.
2. Определить четность, нечетность функции:
 ;
;  - не существует. Область определения не симметрична относительно начала координат, следовательно, функция не является ни четной ни нечетной.
- не существует. Область определения не симметрична относительно начала координат, следовательно, функция не является ни четной ни нечетной.
3. Определить точки пересечения с осью Оу:  ;
;  .
.
4. Определить нули функции (точки пересечения с осью Ох):
 ;
;  ;
;  - нуль функции.
- нуль функции.
5. Определить промежутки знакопостоянства:
 ;
;  ;
;  ;
;  .
.
6. Определить интервалы монотонности, точки экстремума функции:
1) Вычислить первую производную функции:

2) Найти критические точки функции, то есть значения аргумента х, при которых первая производная функции равна нулю:
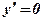 ;
;  ;
;  ;
;  ;
;  .
.
3) Определить знак первой производной слева и справа от критических точек  ;
;  , характер монотонности функции в полученных интервалах, точки экстремума функции:
, характер монотонности функции в полученных интервалах, точки экстремума функции:
| х |  | - 2 |  |  |  | |
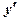 | + | - | - | + | ||
| у | ↑ | - 4 | ↓ | ↓ | ↑ | |
| max | min |
4) Определить экстремальные значения функции:
 ;
;  .
.
7. Определить интервалы выпуклости, точки перегиба графика функции:
1) Вычислить вторую производную функции:




2) Найти критические точки 2-ого рода, то есть значения аргумента х, при которых вторая производная функции равна нулю:
 ;
;  - уравнение корней не имеет, критических точек нет.
- уравнение корней не имеет, критических точек нет.
3) Определить знак второй производной в интервалах области определения функции, характер выпуклости графика функции в них:
| х |  |  |
 | - | + |
| у | Ç | È |
8. Найти дополнительные точки графика функции:
 ;
;  .
.
Пример: Исследовать функцию  и построить ее график.
и построить ее график.
Решение:
1. Найти область определения функции: 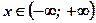 .
.
2. Определить четность, нечетность функции:
 ;
;
 и
и  , следовательно, функция не является ни четной, ни нечетной.
, следовательно, функция не является ни четной, ни нечетной.
3. Определить точки пересечения с осью  .
.
4. Определить нули функции:


 - нули функции.
- нули функции.
5. Определить промежутки знакопостоянства:
 ;
;  ;
;
 ;
;  ;
;
6. Определить интервалы монотонности, точки экстремума функции:
1) Вычислить производную функции:
 .
.
2) Найти критические точки функции:
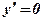 ;
;  ;
;  ;
; 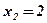 .
.
3) Определить знак производной слева и справа от критических точек  ,
, 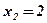 ; характер монотонности функции в полученных интервалах, точки экстремума функции:
; характер монотонности функции в полученных интервалах, точки экстремума функции:
| х |  |  | 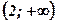 | ||
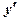 | + | - | + | ||
| у | ↑ | ↓ | ↑ | ||
| max | min |
4) Определить экстремальные значения функции:  ;
;  .
.
7. Определить интервалы выпуклости и точки перегиба графика функции:
1) Вычислить вторую производную функции:
 .
.
2) Найти критические точки 2-ого рода:  ;
;  ;
; 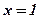 .
.
3) Определить знак второй производной слева и справа от критической точки, характер выпуклости функции в полученных интервалах, точку перегиба графика функции:
| х | 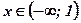 |  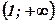 | |
 | - | + | |
| у | Ç | È | |
| перегиб |
 - точка перегиба графика функции.
- точка перегиба графика функции.
8. Найти дополнительные точки графика функции:

Пример: Исследовать функцию  и построить ее график.
и построить ее график.
Решение:
1. Найти область определения функции: 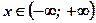 .
.
2. Определить четность, нечетность функции:
 ;
;
 и
и  , следовательно, функция не является ни четной, ни нечетной.
, следовательно, функция не является ни четной, ни нечетной.
3. Определить точки пересечения с осью  .
.
4. Определить нули функции:


 - нули функции.
- нули функции.
5. Определить промежутки знакопостоянства:
 ;
;  ;
;  ;
;  ;
;
6. Определить интервалы монотонности, точки экстремума функции:
1) Вычислить производную функции:
 .
.
2) Найти критические точки функции:
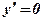 ;
;  ;
;  ;
;  .
.
3) Определить знак производной слева и справа от критических точек  ,
,  ; характер монотонности функции в полученных интервалах, точки экстремума функции:
; характер монотонности функции в полученных интервалах, точки экстремума функции:
| х |  |  |  | ||
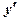 | + | + | - | ||
| у | ↑ | ↑ | 5,4 | ↓ | |
| max |
4) Определить максимальное значение функции:  .
.
7. Определить точки перегиба и интервалы выпуклости графика функции:
1) Вычислить вторую производную функции:
 .
.
2) Найти критические точки 2-ого рода:

 ;
;  ;
;  ;
;  .
.
3) Определить знак второй производной слева и справа от критических точек, характер выпуклости функции в полученных интервалах, точки перегиба графика функции:
| х | 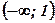 |  |  | ||
 | - | + | - | ||
| у | Ç | È | 3,2 | Ç | |
| перегиб | перегиб |
8. Найти дополнительные точки графика функции:
 ;
;
 .
.
Упражнения: Исследовать функцию и построить ее график:
|
|
|
18. Дифференциал функции. Геометрический смысл дифференциала функции
С понятием производной тесно связано понятие дифференциала.
 Пусть функция
Пусть функция  в точке М0 (х0 , у0) имеет производную
в точке М0 (х0 , у0) имеет производную  . Проведем к графику функции
. Проведем к графику функции  в точке М0 (х0 , у0) касательную М0Т с угловым коэффициентом
в точке М0 (х0 , у0) касательную М0Т с угловым коэффициентом  , который равен значению производной функции
, который равен значению производной функции  в точке х0 :
в точке х0 :  .
.
Если значению аргумента х0 (абсциссе точки М0)дать приращение  , то соответствующее значение функции у0 (ордината точки М0)получит приращение Δу. При этом ордината касательной получит приращение d у.
, то соответствующее значение функции у0 (ордината точки М0)получит приращение Δу. При этом ордината касательной получит приращение d у.
Из прямоугольного треугольника  (
(  ):
):


Определение: Дифференциалом функции  в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента:
в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента:
 .
.
Пример: Вычислить дифференциал аргумента х:  .
.

Вывод:
1. Дифференциал независимой переменной (аргумента) равен приращению этой переменной:  .
.
2. Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной:  или
или  .
.
Вывод: Если функция  имеет производную в точке х0, то дифференциал функции dу в точке х0 равен приращению ординаты касательной, проведенной к графику функции в точке х0 при переходе от х0 к х0 +Δ х.
имеет производную в точке х0, то дифференциал функции dу в точке х0 равен приращению ординаты касательной, проведенной к графику функции в точке х0 при переходе от х0 к х0 +Δ х.
Пример: Найти дифференциалы функций:
1)  ;
;  ;
;
2)  ;
;  .
.
Упражнения: Найти дифференциал функции:
|
|
|
Контрольные вопросы по теме «Дифференциальное исчисление функции одной переменной»
1. Дать определение функции, графика функции.
2. Дать определение области определения функции, множества значений функции.
3. Дать определение четной, нечетной функции.
4. Дать определение монотонной, возрастающей, убывающей функций.
5. Дать определение обратимой функции.
6. Дать определение нулей функции, промежутков знакопостоянства функции.
7. Дать определение периодической функции, периода функции.
8. Дать определение ограниченной функции.
9. Дать определения функции, непрерывной в точке х0, непрерывной на интервале.
10. Дать определение производной функции  в точке х0.
в точке х0.
11. Сформулировать вывод о физическом смысле производной.
12. Сформулировать правила дифференцирования суммы, произведения, частного функций?
13. Дать определение сложной функции.
14. Сформулировать правило дифференцирования сложной функции.
15. Формулы производных основных элементарных функций (степенной, показательной, логарифмической, тригонометрических, обратных тригонометрических).
16. Дать определение касательной к графику функции  в точке М0.
в точке М0.
17. Сформулировать вывод о геометрическом смысле производной.
18. Сформулировать признаки постоянства, возрастания, убывания функции.
19. Дать определения точек экстремума функции (минимума, максимума).
20. Сформулировать признак существования экстремума функции.
21. Как найти наибольшее и наименьшее значения функции на промежутке?
22. Дать определение второй производной функции.
23. Дать определение функции, выпуклой вверх, выпуклой вниз.
24. Дать определение точки перегиба графика функции.
25. Сформулировать признак выпуклости графика функции.
26. Сформулировать признак существования точки перегиба графика функции.
27. Дать определение дифференциала функции.
Таблицы производных
| Производные элементарных функций | Правила дифференцирования |
1. 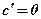 2. 2. 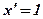 3. 3.  4. 4.  5. 5. 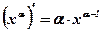 6. 6.  7. 7.  8. 8. 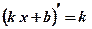 9. 9.  10. 10.  11. 11. 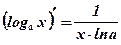 12. 12. 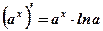 13. 13.  14. 14. 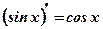 15. 15. 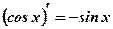 16. 16. 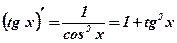 17. 17.  18. 18. 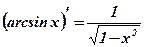 19. 19. 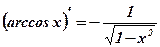 20. 20. 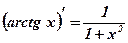 21. 21. 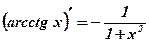 | 1.  2. 2. 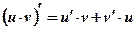 3. 3.  4. 4. 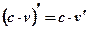 5. 5. 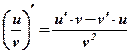 6. 6. 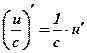 7. 7. 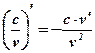 8. 8. 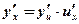 9. 9.  |

 ;
; ;
;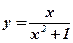 ;
; ;
; .
. ;
; ;
;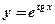 ;
;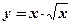 ;
; ;
; ;
; .
.