Построение графиков дифференциальной и интегральной функций распределения
Последовательность построения функции распределения
Для построения графика плотности распределения f(x) ЗНР необходимо либо выбрать из таблицы 1 (приложение 1), либо рассчитать по формуле:
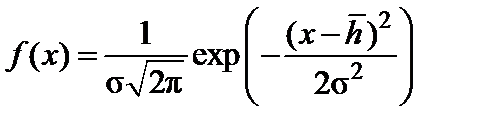(4.1)
плотность распределения для ряда последовательных значений величины износа. Обычно в качестве таких значений принимают середины интервалов статистического ряда. Для более точного построения можно взять в каждом интервале кроме середины еще несколько равноотстоящих точек.
Расчеты целесообразно проводить в табличной форме (табл. 4.1). В столбцы 1, 2 и 6 этой расчетной таблицы переносим значения из статистического ряда (табл. 3.2). В столбец 3 записываем значения табличного аргумента, рассчитанные по формуле (3.2). В столбец 4 записываем найденное в таблице 1 (приложение 1) значение плотности, делим его на σ и результат записываем в столбец 5. Далее строим график, откладывая (в выбранном масштабе) по оси абсцисс данные второго столбца, а по оси ординат – данные пятого столбца.
Для визуальной оценки степени совпадения теоретической плотности распределения с опытными данными на этот же график наносим опытные плотности (столбец 7), полученные делением опытных вероятностей на величину интервала А. На графике они отобразятся в виде горизонтальных линий, каждая из которых занимает весь свой интервал.
Таблица 4.1
Расчет плотности распределения износа плунжера топливного насоса высокого давления (ТНВД)
| Номер интервала | Середина интервала | Табличный аргумент | Плотность вероятности стандартного распределения (табл. 1 приложения 1) | Плотность вероятности исследуемого параметра | Опытная вероятность | Опытная плотность вероятности |
| i | 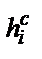 | 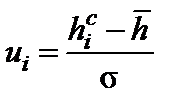 | f(u) | 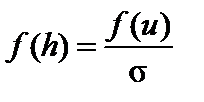 | pi |  |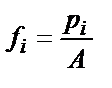
| -2,167 | 0,040 | 0,027 | 0,003 | 0,003 | ||
| -1,468 | 0,137 | 0,095 | 0,125 | 0,125 | ||
| -0,769 | 0,299 | 0,209 | 0,156 | 0,156 | ||
| -0,069 | 0,398 | 0,278 | 0,281 | 0,281 | ||
| 0,629 | 0,329 | 0,230 | 0,187 | 0,187 | ||
| 1,328 | 0,167 | 0,116 | 0,218 | 0,218 |
Для визуальной оценки степени совпадения теоретической плотности распределения с опытными данными на этот же график наносим опытные плотности (столбец 7), полученные делением опытных вероятностей на величину интервала А. На графике они отобразятся в виде горизонтальных линий, каждая из которых занимает весь свой интервал.
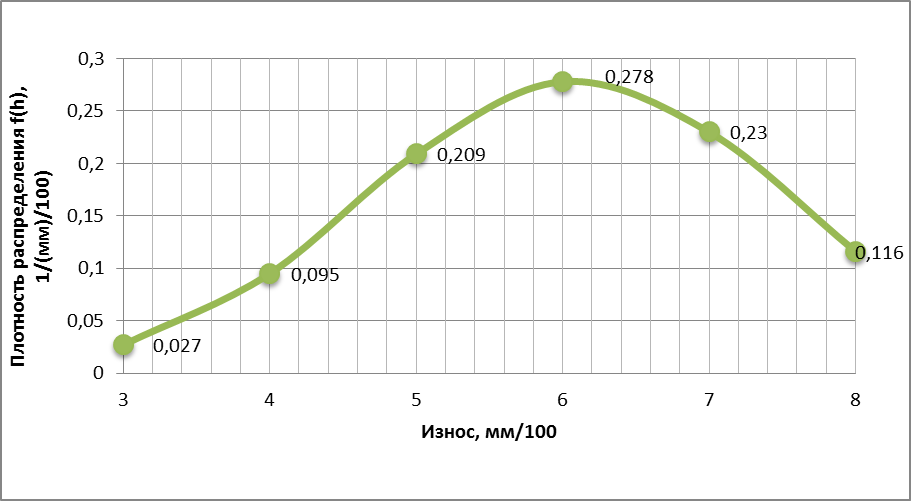Рисунок 4.1 - Теоретическая и опытная плотность распределения износа
плунжера топливного насоса высокого давления (ТНВД)
Для построения графика интегральной функции распределения составляем расчетную табл. 4.2. Содержимое столбцов 1, 2 и 5 (номер интервала, верхняя граница, накопленная опытная вероятность) переносим из статистического ряда (табл. 1.3). В столбец 3 записываем вычисленные по формуле (3.2) значения табличного аргумента u, в столбец 4 – найденные по таблице 2 (приложение 1) значения вероятностей. Откладывая их в масштабе на координатной плоскости и соединяя плавной кривой, получаем график интегральной функции. Для визуальной оценки степени совпадения теоретических значений вероятности с опытными данными на этот же график наносим в том же масштабе накопленные опытные вероятности (столбец 5) в виде отдельных точек.
Таблица 4.2
Расчет значений интегральной функции распределения износа плунжера топливного насоса высокого давления (ТНВД)
| Номер интервала | Верхняя граница интервала | Табличный аргумент | Теоретическая вероятность (таблица 2 приложения 1) | Накопленная опытная вероятность |
| i | 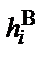 | 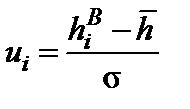 | F(h) = F(u) |  |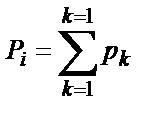
| 3,5 | –1,81 | 0,0351 | 0,031 | |
| 4,5 | –1,11 | 0,1335 | 0,156 | |
| 5,5 | –0,41 | 0,3409 | 0,312 | |
| 6,5 | 0,27 | 0,6064 | 0,593 | |
| 7,5 | 0,97 | 0,8340 | 0,780 | |
| 8,5 | 1,67 | 0,9525 | 0,99 |
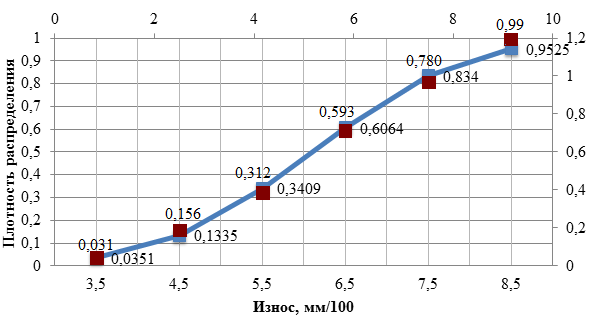
Рисунок 4.2 - Теоретическая интегральная и опытная функция накопленных вероятностей величины износа плунжера топливного насоса высокого давления (ТНВД)