Проверка статистических гипотез

Статистическая гипотеза — это предположение

о виде закона распределения («данная генеральная совокупность нормально распределена»);

о значениях его параметров («генеральное среднее равно нулю»);

об однородности данных («эти две выборки извлечены из одной генеральной совокупности»).

Статистическая проверка гипотезы состоит в выяснении того, согласуются ли результаты наблюдений (выборочные данные) с нашим предположением.

Результатом проверки может быть отрицательный ответ: выборочные данные противоречат высказанной гипотезе, поэтому от нее следует отказаться. В случае ответа неотрицательного (выборочные данные не противоречат гипотезе) гипотезу принимают в качестве одного из допустимых решений (не единственно верного).

Различают основную (нулевую) гипотезу (гипотеза, которая проверяется, 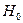) и альтернативную (конкурирующую, противопоставленную основной, 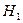). Например, если нулевая гипотеза 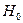: МХ= 10 (т. е. математическое ожидание нормально распределенной величины равно 10), тогда гипотеза 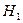, может иметь вид 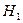: МХ ≠10.

Цель статистической проверки гипотез: на основании выборочных данных принять решение о справедливости основной гипотезы или отклонить в ее пользу альтернативной.

Так как проверка осуществляется на основании выборки, а не всей генеральной совокупности, то существует вероятность, возможно, очень малая, ошибочного заключения.

Так, нулевая гипотеза может быть отвергнута, в то время как в действительности в генеральной совокупности она является справедливой. Такую ошибку называют ошибкой первого рода, а её вероятность — уровнем значимости и обозначают a (стандартные значения a: 0.1, 0.05, 0.01, 0.001). Возможно, что нулевая гипотеза принимается, в то время как в генеральной совокупности справедлива альтернативная гипотеза. Такую ошибку называют ошибкой второго рода, а её вероятность обозначают 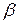Проверка статистических гипотез осуществляется с помощью статистического критерия K — правила (функции от результатов наблюдений), определяющего меру расхождения результатов наблюдений с нулевой гипотезой. Вероятность 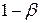называют мощностью критерия.

Замечание. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Например, основная гипотеза состоит в том, что предприятие получает прибыль. Если это правильная гипотеза, то ошибка первого рода состоит в том, что данная гипотеза отвергается. Если принимается решение о том, что прибыль предприятие не получает, то это ошибка второго рода.

Иногда ошибку первого рода называют «альфа-риск» (a-риск) а ошибку второго рода «бета-риск» (b-риск).

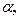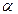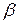Из двух критериев, характеризующихся одной и той же вероятностью выбирают тот, которому соответствует меньшая ошибка 2-го рода, т.е. большая мощность. Уменьшить вероятности обеих ошибок и одновременно можно, увеличив объем выборки.

Значения критерия K разделяются на две части: область допустимых значений (область принятия гипотезы 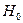) и критическую область (область принятия гипотезы 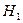). Критическая область состоит из тех же значений критерия К, которые маловероятны при справедливости гипотезы 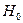. Если значение 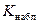критерия K, рассчитанное по выборочным данным, попадает в критическую область, то гипотеза 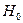отвергается в пользу альтернативной 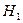в противном случае мы утверждаем, что нет оснований отклонять гипотезу .

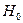Пример 4.7.Для подготовки к зачету преподаватель сформулировал 100 вопросов (генеральная совокупность) и считает, что студенту можно поставить «зачтено», если тот знает 60 % вопросов (критерий). Преподаватель задает студенту 5 вопросов (выборка из генеральной совокупности) и ставит «зачтено», если правильных ответов не меньше трех. Гипотеза 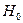: «студент курс усвоил», а множество 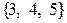— область принятия этой гипотезы. Критической областью является множество 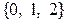— правильных ответов меньше трех, в этом случае основная гипотеза отвергается в пользу альтернативной 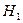«студент курс не усвоил, знает меньше 60 % вопросов».

Студент А выучил 70 вопросов из 100, но ответил правильно только на два из пяти, предложенных преподавателем, — зачет не сдан. В этом случае преподаватель совершает ошибку первого рода.

Студент Б выучил 50 вопросов из 100, но ему повезло, и он ответил правильно на 3 вопроса — зачет сдан, но совершена ошибка второго рода.

Преподаватель может уменьшить вероятность этих ошибок, увеличив количество задаваемых на зачете вопросов.

Алгоритм проверки статистических гипотез сводится к следующему:

1) сформулировать основную 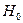и альтернативную 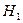гипотезы;

2) выбрать уровень значимости ;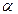

3) в соответствии с видом гипотезы 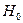выбрать статистический критерий для ее проверки, т.е. случайную величину K, распределение которой известно;

4) по таблицам распределения случайной величины K найти границу критической области 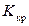(вид критической области определить по виду альтернативной гипотезы );

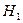5) по выборочным данным вычислить наблюдаемое значение критерия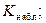

6) принять статистическое решение: если 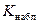попадает в критическую область — отклонить гипотезу 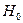в пользу альтернативной 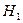; если 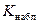попадает в область допустимых значений, то нет оснований отклонять основную гипотезу.

4.3.1 Проверка гипотез о виде распределения. критерий согласия Пирсона

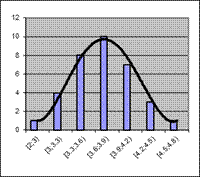
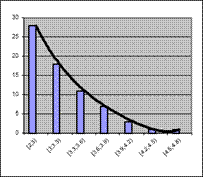
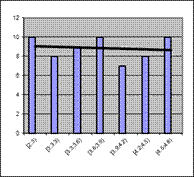
Одной из важных задач математической статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по эмпирическому распределению, представляющему вариационный ряд. Предположение о виде закона распределения можно сделать по гистограмме или полигону (Рис. 4.3)

а)	б)	в)

Рис. 4.3. Возможные виды гистограмм:
а) нормального, б) показательного, в) равномерного распределений

Например, по гистограмме (рис. 4.3, а)) можно сделать предположение о том, что генеральная совокупность распределена по нормальному закону.

Для проверки гипотез о виде распределения служат специальные критерии — критерии согласия. Они отвечают на вопрос: согласуются ли результаты экспериментов с предположением о том, что генеральная совокупность имеет заданное распределение.

Проверим это предположение с помощью критерия согласия Пирсона. В этом критерии мерой расхождения между гипотетическим (предполагаемым) и эмпирическим распределением служит статистика

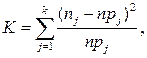
где n — объем выборки;

k — количество интервалов (групп наблюдений);

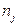— количество наблюдений, попавших в j-й интервал;

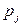— вероятность попадания в j-й интервал случайной величины, распределенной по гипотетическому закону.

Если предположение о виде закона распределения справедливо, то статистика Пирсона распределена по закону «хи-квадрат» с числом степеней свободы 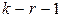(r — число параметров распределения, оцениваемых по выборке):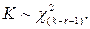

Оцениваются неизвестные параметры с использованием теории точечных оценок (см. источник [3], гл.16 и раздел 3.8. настоящего пособия), некоторые оценки приведены в табл. 4.4.

Таблица 4.4. Оцениваемые параметры и их точечные оценки

Вид распределения	Оцениваемые параметры	Точечные оценки параметров

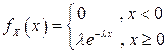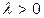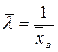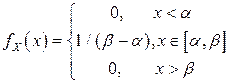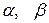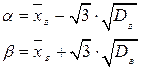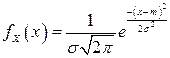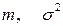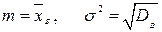Здесь .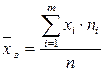

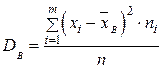Количество интервалов k рекомендуется рассчитывать по формуле Старджеса 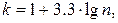где n — объем выборки. Длину i-го интервала принимают равной 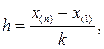где 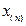—наибольшее, а 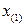— наименьшее значение в вариационном ряду.

Пример 4.8.Длясреднего балла среди 30-ти групп (с точностью до сотых долей балла) получили выборку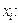

3.7, 3.85, 3.7, 3.78, 3.6, 4.45, 4.2, 3.87, 3.33, 3.76, 3.75, 4.03, 3.8, 4.75, 3.25, 4.1, 3.55, 3.35, 3.38, 3.05, 3.56, 4.05, 3.24, 4.08, 3.58, 3.98, 3.4, 3.8, 3.06, 4.38. Проверить гипотезу о нормальном распределении среднего балла на уровне значимости .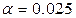

Решение. Сгруппируем эту выборку. Наименьший средний балл равен 3.05, наибольший — 4.75. Интервал [3; 4.8] разобьем на 6 частей длиной 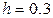, применяя формулу Старджеса ( 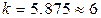). Подсчитаем частоту 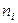(относительную частоту 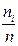) для каждого интервала и получим сгруппированный статистический ряд (табл. 4.5).

Таблица 4.5. Статистический ряд

Интервалы	[3;3.3)	[3.3;3.6)	[3.6;3.9)	[3.9;4.2)	[4.2;4.5)	[4.5;4.8)
Частоты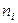
Относительные частоты	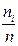0.133	0.233	0.3	0.167	0.1	0.033

Сформулируем основную и альтернативную гипотезы.

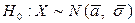— случайная величина X (средний балл) подчиняется нормальному закону с параметрами 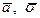. Так как истинных значений параметров 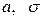мы не знаем, возьмем их оценки, рассчитанные по выборке: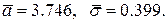

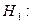случайная величина X не подчиняется нормальному закону с данными параметрами.

Рассчитаем наблюдаемое значение 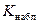статистики Пирсона. Эмпирические частоты 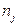уже известны (табл. 4.5), а для вычисления вероятностей 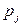(в предположении, что гипотеза 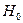справедлива) применим уже известную формулу (свойство В):

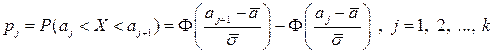
и таблицу функции Лапласа (приложение 1). Полученные результаты сведем в таблицу (табл. 4.6). Наблюдаемое значение статистики Пирсона равно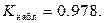

Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение 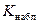, тем сильнее довод против основной гипотезы. Поэтому критическая область для этой статистики всегда правосторонняя: 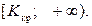Её границу 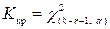находим по таблицам распределения «хи-квадрат» (приложение 3) и заданным значениям 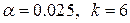(число интервалов), 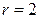(параметры 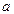и 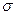оценены по выборке):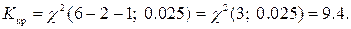

Наблюдаемое значение статистики Пирсона не попадает в критическую область: 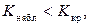поэтому нет оснований отвергать основную гипотезу.

Вывод: на уровне значимости 0.025 справедливо предположение о том, что средний балл имеет нормальное распределение.

Таблица 4.6. Сравнение наблюдаемых и ожидаемых частот

№ п/п	Интервалы группировки	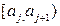Наблюдаемая частота	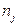Вероятность 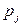попадания в j-й интервал	Ожидаемая частота	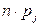Слагаемые статистики Пирсона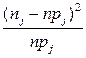
1.	[3; 3.3)		0.101	3.032	0.309
2.	[3.3; 3.6)		0.225	6.761	0.008
3.	[3.6; 3.9)		0.295	8.79	0.166
4.	[3.9; 4.2)		0.222	6.665	0.416
5.	[4.2; 4.5)		0.098	2.946	0.001
6.	[4.5; 4.8)		0.025	0.758	0.077
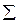	—		0.965	28.95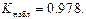

5 Лабораторная работа. Часть 1

Указания. «Показательные» типовые задачи и примеры находятся по указанным разделам.

Задача №1	Тема 2.3
Задача №2	Тема 2.4
Задача №3	Темы 2.5–2.7
Задача №4	Темы 2.8–2.9
Задача №5	Тема 2.10
Задача №6	Тема 2.11
Задачи №7–9	Темы 3.1–3.8

Вариант 1.1

1) Бросаются две игральные кости. Определить вероятность того, что сумма выпавших очков не превосходит трех.

2) В урне три белых и пять черных шаров. Наудачу вынимают два шара. Какова вероятность того, что эти шары разных цветов?

3) Вероятность попадания в цель при одном выстреле равна 0.9. Найти вероятность того, что в результате двух выстрелов будет хотя бы одно попадание.

4) В тире имеется пять винтовок, вероятности попадания в цель из которых равны соответственно 0.5, 0.6, 0,7, 0,8 и 0,9. Найти вероятность попадания в цель из взятой наугад винтовки.

5) 30% изделий некоторого предприятия – продукция высшего сорта. Приобретено 4 изделия этого предприятия. Какова вероятность того, что 2 из них высшего сорта?

6) Найти вероятность того, что среди 300 изделий окажется более трех бракованных, если в среднем бракованные изделия составляют 1,5%.

7) Два стрелка делают по одному выстрелу в одну мишень. Вероятность попадания для первого стрелка равна 0.5, для второго – 0.4. Х– число попаданий в мишень. Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X)и s(Х); в) найти вероятность Р(Х<М(Х)).

8) Дана плотность распределения случайной величины X :

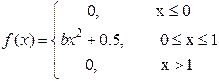
Найти: а) константу b; функцию распределения F(x), в ответ ввести F(l/3); F(l/2); в) МХ; г) DХ; д) Р(1/3 < Х < 1/2).

9) Весы для тяжелых предметов считаются годными, если отклонение X от контрольного веса на более чувствительных весах не превышает 18 г Величина X – нормально распределенная и М(Х)=0, D(X)=10 г. Сколько процентов пригодных весов изготавливает завод? Ответ округлить до целых.

Вариант 1.2

1) На тридцати карточках написаны числа от 11 до 40. Найти вероятность того, что сумма цифр числа на взятой наугад карточке равна 5–ти или 9–ти.

2) Студент знает 50 из 60 вопросов программы. Найти вероятность того, что студент знает два вопроса, содержащиеся в экзаменационном билете.

3) Игральная кость бросается шесть раз. Найти вероятность того, что число выпавших очков ни разу не повторится.

4) Из урны, содержавшей 3 белых и 7 черных шаров, один шар неизвестного цвета утерян. Найти вероятность извлечь наудачу из урны шар белого цвета.

5) Изделия некоторого предприятия содержат 5% брака. Найти вероятность того, что среди пяти взятых наудачу изделий окажутся два бракованных.

6) Полагая вероятность рождения мальчика равной 0.5, найти вероятность того, что среди 200 новорожденных будет: а) 100 мальчиков, б) от 90 до 110 мальчиков.

7) Из коробки, содержащей 3 синих и 4 красных карандаша, наудачу вынимают 3 карандаша. X – число красных карандашей среди вынутых. Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X)и s(Х); в) найти вероятность Р(Х<М(Х)).

8) Задана плотность распределения вероятностей

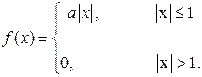
Найти: а) константу а; б) функцию распределения F(x), в ответ ввести значения F(–1/2), F(1/2); в) М(Х); г) D(X); д) Р(–1/2 < X < 2).

9) Компоненты изготовляемого лекарства отвешиваются на весах, ошибка X которых распределена нормально, причём М(Х)= 0, s(Х)= 0.00003 г. Норма веса лекарства 0.02 г. Определить вероятность отбракования лекарства, если максимально допустимый вес принятого к использованию лекарства 0.021г.

Вариант 3

1) В урне 2 красных, 7 зеленых , 5 синих и 10 неокрашенных шаров. Наудачу извлекается один шар. Какова вероятность того, что шар окажется окрашенным?

2) В партии из десяти изделий два бракованных. Наудачу выбирают пять изделий. Какова вероятность того, что среди них одно бракованное?

3) В ящике 10 красных и 6 синих пуговиц. Вынимаются наудачу две пуговицы. Найти вероятность того, что обе пуговицы одного цвета.

4) Имеется десять одинаковых урн, из которых в девяти
находятся по 2 белых и 2 черных шара, а в одной – 5 белых и 1 черный шар. Из взятой наугад урны извлечен белый шар. Какова вероятность того, что шар извлечен из урны, содержавшей 5 белых шаров?

5) Вероятность того, что покупателю потребуется обувь 41–го размера, равна 0,2. Найти вероятность того, что из пяти покупателей только одному потребуется обувь этого размера.

6) Среди семян ржи имеется 0.4% семян сорняков. Какова вероятность при случайном отборе 5000 семян обнаружить 5 семян сорняков?

7) Игральная кость бросается до появления шестерки, но не более семи раз. Х– число бросаний кости. Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X)и s(Х); в) найти вероятность Р(Х<М(Х)).

8) Задана плотность распределения вероятностей

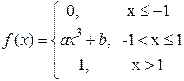
Найти: а) константы а; b б) функцию распределения F(x), в ответ ввести значения F(–1/2), F(1/2); в) М(Х); г) D(X); д) Р(–1/2 < X < 0.5).

9) Изделие считается пригодным, если отклонение его размера от номинала не превышает по модулю 1.45 мм. Случайные отклонения X распределены нормально, причём М(Х)=0, s(Х)=1.5 мм. Определить вероятность того, что случайно взятое изделие является пригодным.

Вариант 4

1) Бросаются две игральные кости. Определить вероятность того, что сумма выпавших очков не превосходит пяти.

2) В урне пять пронумерованных шаров с номерами от 1 до 5. Из урны наугад один за другим вынимаются все шары. Найти вероятность того, что их номера будут идти в возрастающем порядке.

3) Стрелок ведет огонь по приближающейся цели. Вероятность попадания в цель при первом выстреле равна 0.4 и увеличивается на 0.1 для каждого последующего выстрела. Какова вероятность получить два попадания при трех выстрелах?

4) В шкафу стоят однотипные приборы, из которых 15 новых и 10 уже бывших в эксплуатации. Берутся наугад два прибора и эксплуатируются в течение некоторого времени, после чего возвращаются в шкаф. Затем вторично берутся наугад два прибора. Найти вероятность того, что оба вторично взятых прибора новые.

5) Имеется 10 партий изделий, каждая из которых содержит по 20 изделий первого сорта и 5 изделий второго сорта. Из каждой партии берут по изделию. Найти вероятность того, что взяты изделия одного сорта.

6) Какова вероятность того, что в столбике из 100 наугад уложенных монет число монет, расположенных «орлом» вверх, находится в пределах от 45 до 55?

7) Вероятность попадания мячом в корзину при каждом бросании равна 0,4. Х– число попаданий при пяти бросках. Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X) и s(Х); в) найти вероятность Р(Х<М(Х)).

8) Задана плотность распределения вероятностей

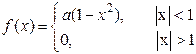
Найти: а) константу а; б) функцию распределения F(x); в ответ ввести значения F(0), F(1/2); в) М(Х),; г) D(X); д) Р(0 < X < 0.5).

9) Случайные ошибки измерителя глубины распределены по нормальному закону. Какую среднеквадратическую ошибку должен иметь измеритель глубины, чтобы с вероятностью 0.7 ошибка измерения глубины по модулю была меньше 150 м.

Вариант 5

1) На сорока карточках написаны числа от 21 до 60. Найти вероятность того, что сумма цифр числа на взятой наугад карточке равна пяти или восьми.

2) Слово «интеграл» составлено из букв разрезной азбуки. Из этих восьми карточек наудачу извлекают четыре и складывают в ряд друг за другом в порядке появления. Какова вероятность получить при этом слово «игра»?

3) Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0.96 для первого сигнализатора и 0.98 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.

4) На складе вперемешку хранятся лампы, полученные с четырех заводов: 250 – с первого завода, 525 – со второго, 275 –с третьего и 950 – с четвертого. Вероятность того, что лампа проработает больше 1500 часов, для продукции этих заводов соответственно равна 0.15, 0.3, 0.2 и 0.1. Найти вероятность того, что взятая наугад лампа проработает больше 1500 часов.

5) Имеется пять одинаковых партий изделий. Каждая партия состоит из четырех изделий первого сорта и одного изделия второго сорта. Из каждой партии берут по изделию. Найти вероятность того, что среди выбранных изделий хотя бы три изделия первого сорта.

6) Вероятность для любого абонента позвонить на коммутатор в течение часа равна 0.02. Телефонная станция обслуживает 250 абонентов, Какова вероятность того, что в течение часа позвонят три абонента?

7) Монета подбрасывается шесть раз. X – произведение
числа выпадений «орла» на число выпадений «решки». Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X) и s(Х); в) найти вероятность Р(Х<М(Х)).

8) Случайная величина 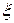имеет плотность распределения

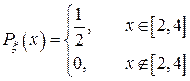
Другая случайная величина связана с 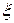функциональной зависимостью 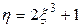. Определить математическое ожидание 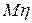и дисперсию 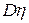случайной величины .

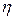9) Средняя дальность полёта снаряда равна т. Предполагается, что дальность полёта X распределена по нормальному закону со средним квадратичным отклонением 100 м. Найти, какой процент снарядов даёт перелёт от 120 м до150 м.

Вариант 6

1) В урне 10 белых, 15 синих и 25 красных, шаров. Найти вероятность того, что взятый наудачу шар окажется белым.

2) В урне 2 белых, 3 черных и 5 синих шаров. Наудачу извлечены три шара. Какова вероятность того, что все три шара разных цветов?

3) Деталь проходит три операции обработки. Вероятность получения брака на первой операции равна 0.02, на второй – 0.03, на третьей – 0.04. Найти вероятность получения детали без брака после трех операций.

4) На склад поступило 200 подшипников с первого завода, 460 – со второго и 340 – с третьего. Вероятность брака в продукции первого завода равна 0.03, второго – 0.02, третьего – 0.01. Взятый наугад подшипник оказался бракованным. Найти вероятность того, что он изготовлен на первом заводе.

5) Вероятность изготовления годной детали равна 0.7, а вероятность того, что годная деталь первого сорта равна 0.3. Наудачу взято 5 деталей. Найти вероятность того, что среди них ровно три детали первого сорта.

6) Производство дает 1% брака. Какова вероятность того, что из взятых на исследование 1100 изделий выбраковано будет не более чем 17 изделий?

7) В партии из десяти деталей имеется 8 стандартных. Наугад взято 4 детали. X – число стандартных деталей среди взятых деталей. Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X) и s(Х); в) найти вероятность Р(Х<М(Х)).

8) Случайная величина 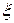имеет плотность распределения

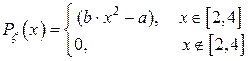
Найти a, b. Другая случайная величина связана с 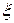функциональной зависимостью 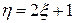. Определить математическое ожидание 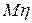и дисперсию 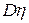случайной величины .

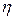9) Завод изготавливает бруски. Номинальный размер (длина) бруска d = 15 мм. Фактический диаметр – случайная величина с математическим ожиданием 15.5 мм и среднеквадратическим отклонением 0.3 мм. При контроле бракуются все бруски, диаметр которых отличается от номинала более, чем на 0.1 мм. Определить процент брака.

Вариант 7

1) Бросаются две игральные кости. Определить вероятность того, что сумма выпавших очков не превосходит семи.

2) В партии из 50 изделий 6 бракованных. Из партии выбираются наудачу 5 изделий. Определить вероятность того, что среди этих пяти изделий два бракованных.

3) В партии 20 изделий, из них 7 нестандартных. Наудачу взято 5 изделий. Найти вероятность того, что среди выбранных изделий хотя бы два нестандартных.

4) Среди двадцати пяти экзаменационных билетов пять «хороших». Найти вероятности того, что: а) первый студент взял «хороший» билет; б) второй студент взял «хороший» билет.

5) Найти вероятность того, что при десяти бросаниях монеты «орел» выпадет пять раз.

6) В магазин отправлено 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка будет разбита, равна 0.003. Найти вероятность того, что магазин получит хотя бы одну разбитую бутылку.

7) В ящике лежат пять изделий, из которых одно бракованное. Из ящика извлекают изделия одно за другим до тех пор, пока не будет вынуто бракованное изделие. X – число вынутых изделий. Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X) и s(Х); в) найти вероятность Р(Х<М(Х)).

8) Задана плотность распределения вероятностей

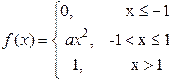
Найти: а) константу а; б) функцию распределения F(x), в ответ ввести значения F(–1/3), F(1/3); в) М(Х), г) D(X); д) Р(–1/2 < X < 0.5).

9) Случайная величина X – отклонение размера изделия от нормы – нормально распределенная, причём М(Х)= 0. Найти s(Х), если известно, что Р(– 1<X<1) = 0.3.

Вариант 8

1) Наудачу выбрано натуральное число, не превосходящее 20. Какова вероятность того, что это число кратно 5?

2) Слово «математика» составлено из букв разрезной азбуки. Наудачу извлекают отсюда три буквы и располагают друг за другом в порядке извлечения. Какова вероятность того, что при этом получится слово «мак»?

3) Из колоды, содержащей 36 карт, вынимают наудачу четыре карты. Найти вероятность того, что среди взятых карт есть хотя бы один туз.

4) Имеется три урны. Первая содержит 2 белых и 3 черных шара, вторая – 4 белых и 1 черный, третья – 3 белых шара. Наугад берется урна и из нее извлекается шар. Найти вероятность того, что извлечен белый шар.

5) Сделано 14 выстрелов по цели. Вероятность попадания при каждом выстреле равна 0.2. Найти вероятность того, что произошло три попадания в цель.

6) Вероятность появления события А в каждом из 1500 испытаний равна 0.4. Найти вероятность того, что число появлений события А заключено между: а) 570 и 630, б) 600 и 660.

7) Игральную кость бросают пять раз. X – число выпадений шести очков. Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X) и s(Х); в) найти вероятность Р(Х<М(Х)).

8) Дана плотность распределения случайной величины X :

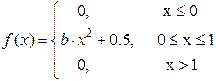
Найти: а) константу b; функцию распределения F(x), в ответ ввести F(l/3); F(l/2); в) М(X); г) D(X); д) Р(0.3 < х < 0.9).

9) Деталь, изготовленная автоматом, считается годной, если отклонение X её контролируемого размера от номинала не превышает 18 мм. Величина X распределена нормально, причём s(Х)=9 мм. Найти вероятность того, что деталь будет признана годной.

Вариант 9

1) Все буквы русского алфавита написаны на 33–х карточках. Наудачу извлекается одна карточка. Найти вероятность того, что на этой карточке написана гласная буква.

2) В урне 6 белых и 4 черных шара. Из урны наудачу извлечены 5 шаров. Найти вероятность того, что среди них 2 белых и 3 черных.

3) Рабочий обслуживает три станка. Вероятность того, что в течение часа станок потребует внимания рабочего, для первого станка равна 0.9, для второго – 0.8. для третьего – 0.7. Найти вероятность того, что в течение часа по крайней мере один из станков потребует внимания рабочего.

4) В первой урне – 1 белый и 2 черных шара, во второй – 3 белых и 3 черных шара. Из второй урны наугад переложили в первую один шар, а затем из первой урны вынули наугад один шар. Найти вероятность того, что вынутый шар находился ранее во второй урне, если известно, что он белый.

5) Партия изделий содержит 5% брака. Найти вероятность того, что среди пяти взятых наудачу изделий: а) нет ни одного бракованного, б) два бракованных изделия.

6) Вероятность производства бракованной детали равна 0.008. Какова вероятность наиболее вероятного числа бракованных деталей среди наудачу отобранных тысячи деталей?

7) Игральную кость бросают дважды. Х– абсолютная величина разности выпавших очков. Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X) и s(Х); в) найти вероятность Р(Х<М(Х)).

8) Случайная величина 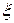имеет плотность распределения

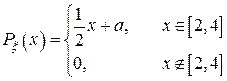
Найти а. Другая случайная величина связана с 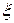функциональной зависимостью 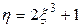. Определить математическое ожидание 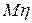и дисперсию 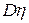случайной величины .

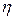9) Средняя дальность полёта пули равна 2т. Предполагается, что дальность полёта X распределена по нормальному закону со средним квадратичным отклонением 90 м. Найти, какой процент снарядов даёт перелёт от 100 м до 110 м.

Вариант 10

1) Бросаются две игральные кости. Определить вероятность того, что сумма выпавших очков не превосходит девяти.

2) При наборе телефонного номера абонент забыл две последние цифры и набрал их наугад, зная, что эти цифры нечетные и разные. Найти вероятность того, что номер набран правильно.

3) Имеется две одинаковых партии изделий, содержащих по семи изделий первого сорта и по одному изделию второго сорта. Из каждой партии берут по четыре изделия. Найти вероятность того, что состав партий останется одинаковым.

4) В группе из десяти студентов, пришедших на экзамен, три студента подготовлены отлично, четыре – хорошо, два – посредственно и один – плохо. Отлично подготовленный студент знает все 20 вопросов экзаменационных билетов, хорошо подготовленный – 16, посредственно подготовленный – 10, плохо подготовленный – 5. Вызванный наугад студент ответил на все три вопроса билета. Найти вероятность того, что этот студент подготовлен отлично.

5) Имеется 7 одинаковых партий изделий. Каждая партия состоит из пяти изделий первого сорта и трех изделий второго сорта. Из каждой партии берут наудачу по одному изделию. Найти вероятность того, что взято не более одного изделия второго сорта.

6) Опыт состоит в бросании монеты 4040 раз (опыт Бюффона), «орел» выпал 2048 раз. Найти вероятность того, что при повторении опыта Бюффона относительная частота появления «орла» отклонится от 0.5 не более чем в опыте Бюффона.

7) Вероятность попадания при каждом выстреле равна 0,7. Охотник стреляет до первого попадания, но успевает сделать не более пяти выстрелов. X – число произведенных выстрелов. Требуется для дискретной случайной величины X: а) построить ряд распределения; б) вычислить М(Х), D(X) и s(Х); в) найти вероятность Р(Х<М(Х)).

8) Дана плотность распределения случайной величины X :

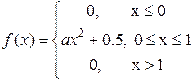
Найти: а) константу а; функцию распределения F(x), в ответ ввести F(1.3); F(0.5); в) МX; г) DX; д) Р(0.3 < X < 0.8).

9) Производится стрельба по цели, имеющей вид полосы шириной 25 м. Прицеливание производится по средней линии полосы. Среднеквадратическое отклонение точки попадания от середины полосы равно 16 м. Найти вероятность попадания в полосу при одном выстреле.

Вариант 11

1) Наудачу выбрано натуральное число, не превосходящее 20. Какова вероятность того, что 20 нацело делится на это число ?

2) Из пяти карточек с буквами А, Б, В, Г, Д наудачу выбирают три. Какова вероятность того, что из этих трех карточек можно составить слово «ДВА»?

3) Партия состоит из четырех изделий первого сорта и шести изделий второго сорта. Наудачу взято три изделия. Какова вероятность того, что ровно два из них одного сорта?

4) В урне лежит один шар неизвестного цвета – с равной вероятностью белый или черный. В урну опускается белый шар и затем наудачу извлекается один шар, оказавшийся белым. Какова вероятность того, что в урне остался белый шар?

5) Имеется пять одинаковых партий изделий. Каждая партия состоит из двух изделий