Проверка статистических гипотез

Приведем список некоторых основных пакетов, содержащих стандартные статистические тесты (многие критерии находятся в пакете stats, который загружается автоматически):

ctest - классические тесты (Фишера, "Стьюдента", Пирсона, Бартлетта, Колмогорова- Смирнова...)

eda - методы, используемые в “Разведочном анализе данных”

lqs - регрессия и оценка ковариации

modreg – современные методы построения регрессионных моделей: сглаживание и локальные регрессии

mva - многомерный анализ

nls – нелинейные модели регрессии

splines - сплайны

stepfun - эмпирические функции распределения

ts - исследования временных рядов

Для загрузки пакета используется фукция: library() с именем соответствующего пакета:

> library(eda)

3.1. Критерий Х² Пирсона (Проверка гипотезы о нормальном распределении генеральной совокупности ).

Описание

Критерий c2 используется для анализа таблиц сопряженности признаков и сравнения законов распределения непрерывных случайных величин. Анализируются номинальные или приведенные к номинальной шкале данные, представленные в виде таблицы сопряженности признаков. Для непрерывных случайных величин используется принадлежность значений заданным интервалам, выбираемых таким образом, чтобы в каждом из них было не менее 5-7 значений (интервалы с меньшим числом значений объединяются). Простейшим выбором является равный шаг интервалов, равный 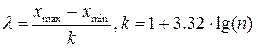или .

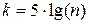Вычисление критериальной статистики производится по формуле:

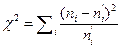
где n_i- эмпирические частоты, n_i^’- теоретические частоты попадания элементов выборки в группы (заданные интервалы).

Число степеней свободы находят по формуле:

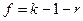
где 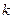-число групп выборки, 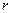-число параметров предполагаемого распределения, которые оценены по данным выборки.

Если предполагаемое распределение – нормальное, то по выборке оценивают два параметра (математическое ожидание и дисперсию), поэтому 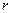=2 и 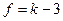.Одной из функций, осуществляющей проверку данного критерия в R является chisq.test().

Описание функции

chisq.test (x, y = NULL, p = rep(1/length (x), length (x)))

Параметры

x	вектор или матрица.
y	вектор; игнорируемый, если x - матрица.
p	вектор теоретических вероятностей той же длины, что x.

Примечание

Если x ‑ матрица с одной строкой или столбцом, или если x ‑ вектор, и y не дан, x ‑ одномерная таблица сопряженности признаков. В этом случае, проверенная гипотеза - равняются ли вероятности совокупности тем, что в p, или все равны, если p не дается. Если x - матрица с двумя строками (или столбцами), содержащими неотрицательные целые числа, то она рассматривается как таблица сопряженности признаков. Если x и y – два вектора, содержащих факторы (номинальные или ординальные значения), то по ним строится таблица сопряженности.

Критические значения (квантили) находятся с использованием функции qchisq(p,df) или по таблице c2-распределения [2,стр.329].

Пример

Сгенерируем случайную выборку из нормального распределения, и проверим ее нормальность.

N<-100 # объем выборки

x.norm<-rnorm(N,mean=2,sd=2.5) # задаем среднее и СКО

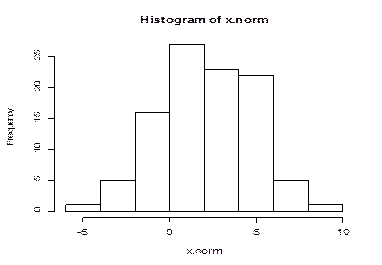Вычисляем квантили выборки с шагом 10% (по 10 элементов в интервале)

> x.norm.q <- quantile(x.norm,probs=seq(0,1,0.1))

> round(x.norm.q,2)

0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%

-4.12 -1.51 -0.14 0.59 1.52 2.15 2.70 3.89 4.51 5.22 8.15

> summary(x.norm)

Min. 1st Qu. Median Mean 3rd Qu. Max.

-1.4490 0.6675 2.0330 2.0670 3.1050 6.5830

Выбираем интервалы:

> k<-6 # число интервалов

> x.q <- c(-10, -1.0, 0.5, 2.0, 3.5, 5.0,12.0)

Вычисляем фактические частоты

> x.norm.hist<-hist(x.norm,breaks=x.q,plot=FALSE)

> x.norm.hist$counts

12 15 22 18 18 15

Вычисляем (по выборке) теоретические вероятности для каждого интервала

> x.q[1]<-(-Inf);x.q[k+1]<-(+Inf)#«раздвигаем» границы до бесконечности

> x.norm.p.theor<-pnorm(x.q,mean=mean(x.norm),sd=sd(x.norm))

> x.norm.p.theor<-(x.norm.p.theor[2:(k+1)]-x.norm.p.theor[1:k])

> round(x.norm.p.theor,2)

0.12 0.15 0.21 0.22 0.16 0.14

Сравниваем фактические и теоретические частоты

> chisq.test(x.norm.hist$counts,p=x.norm.p.theor)

Chi-squared test for given probabilities

data: x.norm.hist$counts

X-squared = 0.9691, df = 5, p-value = 0.965

Поскольку для проверки нулевой гипотезы H₀ о нормальности распределения генеральной совокупности в нашем случае используется правосторонний критерий, а уровень значимости (p-value) равен 0.965 (96.5%), то нужно допустить разрешить вероятность ошибки, равную 96.5%, чтобы считать выборку не принадлежащей нормальному распределению. Следовательно, гипотеза о нормальности принимается.

Приведем пример проверки случайности сопряжения признаков. Пусть первый признак является полом (закодированным символами «М» и «Ж»), а второй – наличием близорукости (закодированной числами 0, 1).

> x<-c(”М”,”Ж”,”Ж”,”М”,”Ж”,”Ж”,”М”,”Ж”,”М”,”Ж”,”Ж”,”М”,”М”)

> y<-c( 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0)

> tbl<-table(x,y)

> tbl

y

x 0 1

Ж 4 3

М 4 2

Оцениваем по выборке маргинальные (безусловные) вероятности для x и y:

> p.x<-c(sum(tbl[1,])/sum(tbl),sum(tbl[2,])/sum(tbl))

> p.y<-c(sum(tbl[,1])/sum(tbl),sum(tbl[,2])/sum(tbl))

или, что тоже самое (годится для таблиц любой размерности),

> p.x<-apply(tbl,1,sum)/sum(tbl) # 1 - суммируем по строкам

> p.y<-apply(tbl,2,sum)/sum(tbl) # 2 - суммируем по столбцам

Если сопряженности признаков нет (гипотеза H₀), то наблюдаемые относительные частоты должны совпадать с произведениями маргинальных вероятностей:

>p.theor<-c(p.x[1]*p.y[1],p.x[2]*p.y[1], p.x[1]*p.y[2],p.x[2]*p.y[2])

или, что тоже самое (годится для таблиц любой размерности),

> p.theor<- p.x %*% t(p.y)

> chisq.test(as.vector(t),p=p.theor)

Chi-squared test for given probabilities

data: as.vector(t)

X-squared = 0.1238, df = 3, p-value = 0.9888

Поскольку p-value близко к единице, то нулевая гипотеза принимается. Отметим, что поскольку в таблице сопряженности tbl есть ячейки с числами, меньшими 5 (в нашем случае – все ячейки такие), то аппроксимация хи-квадрат может быть неправильной, а полученный результат - неверным.