Произведение и сумма событий

Произведением двух событий А я В называется событие АВ, состоящее в том, что происходит каждое из этих событий.

Произведением нескольких событий называется событие, состоящее в появлении всех этих событий.

Суммой двух событий А и В называется событие А+В, состоящее в том, что происходит хотя бы одно из этих событий.

Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Пример 2.9. Из урны, содержащей не менее двух белых и двух черных шаров, последовательно извлекаются два шара.

А = {белый шар при первом извлечении};

В = {белый шар при втором извлечении};

АВ = {белые шары при первом и втором извлечениях};

А+В = {первый шар – белый, второй – черный, или первый шар – черный, второй – белый, или первый и второй шары – белые}.

Условная вероятность. вероятность произведения событий

Определение2.2.Вероятность события А, вычисленная при условии, что произошло событие В, называется условной вероятностью события А при наличии события В и обозначается Р(А|В).

Пример 2.10. Опыт: подбрасывание двух монет. События:

А = {выпадение «орла» на обеих монетах};

В = {выпадение «орла» на одной из монет}.

Найти вероятность Р(А). Общее число возможных исходов опыта n=4 (оо, ор, рр, ро), благоприятствующий исход один (оо), следовательно, Р(А)=1/4.

Найти теперь условную вероятность Р(А|В). Поскольку известно, что произошло событие В, число возможных исходов испытания п–1(оо, ор, ро), благоприятствующий исход по–прежнему один, следовательно, Р(А|В)=1/3.

Теорема. Вероятность произведения двух событий А и В, равна произведению вероятности одного из этих событий на условную вероятность другого при наличии первого:

Р(АВ) = Р(А)Р(В|А)или Р(АВ) = Р(В)Р(А|В). (2.1)

Эта теорема обобщается на любое конечное число событий следующим образом:

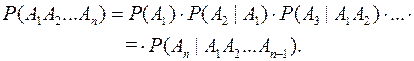(2.2)

Определение2.3. Два события называются независимыми, если появление любого из них не изменяет вероятности другого, т.е. события А и В независимы, если Р(А|В)=Р(А).

Из формул (2.1) следует, что если выполняется равенство Р(А|В)=Р(А),.то выполняется и равенство Р(В\А)=Р(В).

Определение2.4.Несколько событий, А₁, А₂, ..., А_п, называются независимыми в совокупности (или просто независимыми), если появление любых из них не изменяет вероятностей остальных. Для независимых событий формула (2.2) принимает вид:

Р(А₁ А₂...А_п) = Р(А₁)×Р(А₂×...×Р(А_п).

Пример 2.11. Из урны, содержащей 3 белых и 7 черных шаров, наудачу извлекают два шара. Найти вероятность того, что оба шара белые.

Решение. Считаем, что шары извлекаются поочередно. Пусть

А = {первый шар – белый}, В = {второй шар – белый}, тогда АВ – {оба шара – белые}.

По теореме умножения вероятностей Р(АВ)=Р(А)Р(В|А). Согласно классическому определению вероятности Р(А)=3/10, Р(В|А)=2/9.Следовательно, Р(АВ)= (3/10)×(2/9).

Пример 2.12. Два стрелка стреляют по одной мишени. Вероятность поражения мишени первым стрелком равна 0.6, вторым – 0.8. Найти вероятность того, что в мишени будет две пробоины.

Решение. Введем в рассмотрение события, вероятности которых известны:

А = {поражение мишени первым стрелком},

В – {поражение мишени вторым стрелком}.

Интересующее нас событие выразим через эти события. Для того, чтобы имело место событие С={две пробоины в мишени}, надо, чтобы произошли вместе события А и В, т.е. С=АВ.

Естественно считать события А и В независимыми, поэтому

Р(С)=Р(А)×Р(В)=0.6×0.8.

Вероятность суммы событий

Теорема 2.1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

Теорема 2.2. Для любого события А вероятность противоположного события А выражается равенством

Р(`А) = 1 – Р(А)

Теорема 2.3. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления:

Р(А + В) = Р(А)+ Р(В) – Р(АВ).

Теорема сложения обобщается на любое конечное число событий следующим образом:

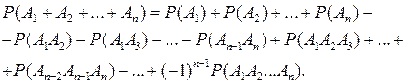(2.3)

Если события А₁, А₂, ..., А_ппопарно несовместные, то формула (2.3) принимает вид:

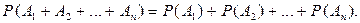
Замечание. При решении задач с использованием формулы (2.3) приходится производить громоздкие вычисления, поэтому часто выгоднее перейти к противоположным событиям, т.е. вместо вероятности суммы событий А₁+А₂+...+А_п находить вероятность произведения противоположного события 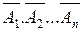. Очевидно, что эти два события противоположны, поэтому

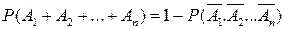(2.4)

Пример 2.13. В условиях примера 2 предыдущего пункта найти вероятность появления хотя бы одной пробоины.

Решение. Данное событие есть сумма событий А и В, причем эти события совместные, поэтому вероятность интересующего нас события равна Р(А + В) = Р(А) + Р(В) – Р(АВ). Ранее было найдено, что Р(АВ)=0.48, следовательно, Р(А + В) = 0.6 + 0.8 – 0.48 = 0.92.

Пример 2.14. Устройство содержит четыре независимо работающих элемента и сохраняет работоспособность, если работает хотя бы один из элементов. Вероятности безотказной работы элементов в течение определенного срока соответственно равны 0.9, 0.8, 0.7 и 0.6. Найти вероятность безотказной работы устройства.

Решение. Пусть события А₁ А₂, А₃и А₄означают безотказную работу соответственно первого, второго, третьего и четвертого элементов. Событие А={безотказная работа устройства} есть сумма событий: А=А₁+А₂+А₃+А₄.События А₁ А₂, А₃и А₄совместные, поэтому вероятность Р(А)надо вычислять по формуле (2.3). Чтобы упростить вычисления, воспользуемся формулой (2.4):

.

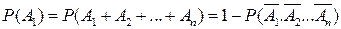Так как события А₁ А₂, А₃и А₄независимые, то противоположные события 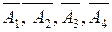также независимы, поэтому

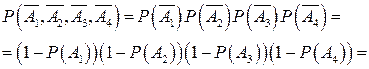
= (1 – 0.9)(1 – 0.8)(1 – 0.7)(1 – 0.6) = 0.0024; и

Р(А) = 1 – 0.0024 = 0.9976.

Пример 2.15. Производится три независимых выстрела по мишени. Вероятности попадания в мишень при первом, втором и третьем выстрелах соответственно равны 0.2, 0.5, 0.4. Найти вероятность того, что будет ровно два попадания в мишень.

Решение. Событие А={ровно два попадания в мишень} выражается через события А₁={попадание при первом выстреле}, А₂={попадание при втором выстреле), А₃={попадание при третьем выстреле} следующим образом:

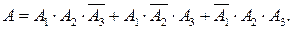
Отсюда, учитывая несовместность суммируемых произведений событий и независимость событий А₁, А₂, А₃,находим

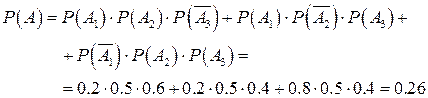
Пример 2.16. В двух урнах находятся шары, отличающиеся только цветом: в первой урне 5 белых шаров, 11 черных и 8 красных, во второй 10 белых, 8 черных и 6 красных. Из обеих урн наудачу извлекают по одному шару. Найти вероятность того, что оба шара одного цвета.

Решение. Введем в рассмотрение следующие события:

В₁={извлечение белого шара из первой урны},

В₂={извлечение белого шара из второй урны},

С₁={извлечение черного шара из первой урны},

С₂={извлечение черного шара из второй урны},

D₁={извлечение красного шара из первой урны},

D₂={извлечение красного шара из второй урны}.

Выразим событие А= {извлечение шаров одного цвета} через эти события:

А= В₁ В₂+ С₁ С₂+ D₁ D₂

Следовательно,

Р(А) = Р(В₁)Р(В₂) + Р(С₁)Р(С₂) + Р(D₁)P(D₂).

Вероятности событий В, С, D найдем из классического определения: Р(В₁)=5/24, Р(В₂)=10/24, Р(С₁)=11/24, Р(С₂)=8/24, Р(D₁)=8/24, P(D₂)=6/24.

Таким образом, получаем

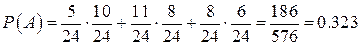
Формула полной вероятности

Пусть А – некоторое событие, которое может появиться совместно с одним из ряда попарно несовместных событий Н₁, Н₂,…,Н_n образующих полную группу ( 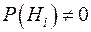). Будем называть события Н гипотезами.

Теорема 2.4. Вероятность события А, которое может произойти вместе с одной из гипотез Н₁, Н₂,…,Н_n, равна сумме парных произведений вероятностей этих гипотез на соответствующие им условные вероятности события А:

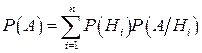
Эта формула называется формулой полной вероятности.

Пример 2.17.Первый станок производит 25%, второй – 35%, третий – 40% всех изделий. Брак в их продукции составляет соответственно 5%, 4% и 2%. Найти вероятность того, что взятое наугад изделие окажется бракованным.

Решение. Введем гипотезы:

Н₁={взятое изделие изготовлено на первом станке},

Н₂={взятое изделие изготовлено на втором станке},

Н₃={взятое изделие изготовлено на третьем станке}.

События Н₁, Н₂и Н₃ несовместные, образуют полную группу, и событие А ={взятое изделие – брак} происходит вместе с одним из них, следовательно, они действительно могут быть взяты в качестве гипотез для события А. Согласно формуле полной вероятности

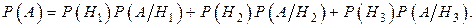
По условию задачи

Р(Н₁)= 0.25, Р(Н₂)=0.35, Р(Н₃)=0.40, 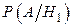=0.05,

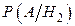=0.04, 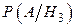=0.02,

следовательно, Р(А)= 0.25 • 0.05 + 0.35 • 0.04 + 0.40 • 0.02 = 0.0345.

Замечание. Вероятности 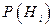характеризуют возможность осуществления некоторых условий 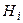, а 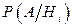возможность появления А при этих условиях.

Формула Байеса

Пусть событие А может произойти совместно с одной из гипотез Н₁, Н₂,…, Н_n . Если до проведения опыта были известны вероятности гипотез 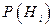, а в результате опыта произошло событие А, то условные вероятности гипотез 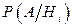вычисляются по формуле Байеса:

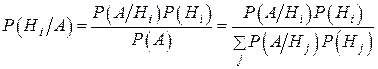
Пример 2.18.Первый станок производит 20%, а второй 80% всех деталей. Брак в их производстве составляет соответственно 4% и 2%. Взятая наугад деталь оказалась бракованной. Найти вероятность того, что эта деталь изготовлена на первом станке.

Решение. Введем две гипотезы для события А={взятая деталь оказалась бракованной}:

Н₁={взятая деталь изготовлена на первом станке},

Н₂={взятая деталь изготовлена на втором станке}.

Из условия задачи известно: Р(Н₁)= 0.2, Р(Н₂)=0.8, 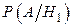=0.04, 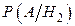=0.02.. По формуле Байеса находим

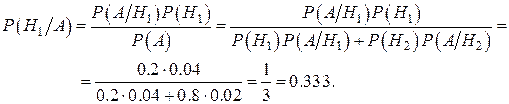
Замечание. Формула Байеса указывает путь использования новых экспериментальных данных для коррекции априорных (доопытных) вероятностных представлений об исследуемом объекте.