Теоремы о дифференцируемых функциях.

Теоремы о дифференцируемых функциях.

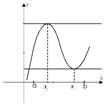
Теорема Ферма.

Пусть функция определена и дифференцируема

на интервале (a;b) и в некоторой точке x₀ этого интервала принимает наибольшее или наименьшее значение. Тогда .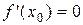

Геометрический смысл теоремы Ферма:

Так как 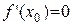, то угловой коэффициент касательной равен нулю 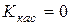Þ касательная параллельна оси ОХ.

Теорема Ролля.

Пусть функция 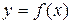определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), причем на концах интервала принимает одинаковые значения 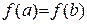. Тогда существует точка сÎ(a;b), значения производной в которой равно 0, т.е. .

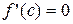Геометрический смысл теоремы Ролля:

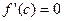Þ К_кас=0 Þ касательная

в точке c параллельна оси ОX.

Теорема Лагранжа.

Пусть функция 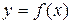определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда существует точка cÎ(a;b), значение производной в которой равно .

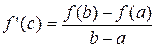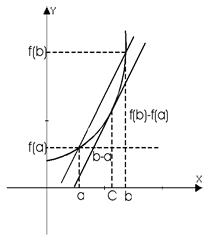
Геометрический смысл теоремы Лагранжа:

.

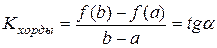Существует точка cÎ(a;b), в которой угловой коэффициент касательной равен угловому коэффициенту хорды, соединяющей граничные точки:

.

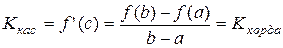Найдется такая точка на графике, касательная в которой параллельна хорде, стягивающей концы отрезка [a;b].

Теорема Коши.

Пусть функции f(x) и g(x) определены и непрерывны на отрезке [a;b] и дифференцируемы на интервале (a;b), причем производная функции g(x) отлична от нуля, g¢(x)¹0. Тогда существует такая точка cÎ(a;b), для которой выполняется равенство: .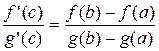

Правило Лопиталя.

Теорема.

Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки x₀, за исключением может быть самой точки x₀, и 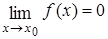, 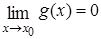. Тогда если существует предел отношения производных функций 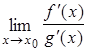, то существует предел отношения самих функций 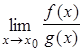, причем они равны между собой, т.е. .

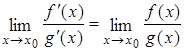В дальнейшем это утверждение будем также называть правилом Лопиталя

Замечание. На практике при раскрытии неопределенности типа 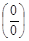можно пользоваться правилом Лопиталя и в случаях, когда x®±¥, x®¥.

Для раскрытия неопределенностей типа 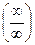существует аналог правила Лопиталя.

Замечание 1. Правилом Лопиталя можно пользоваться при раскрытии неопределенностей вида (¥-¥), (0×¥), (1^¥), (¥⁰), (0⁰), сводя их к неопределенностям типа , .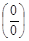

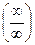Замечание 2. Если после применения правила Лопиталя опять получаем неопределенность вида 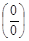или 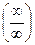, то его можно применить повторно.

Пример: Вычислить пределы по правилу Лопиталя.

1. Чтобы применять правило Лопиталя при неопределенности вида 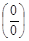или 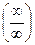, нужно продифференцировать отдельно числитель и знаменатель дроби, и вычислить полученный предел.

.

.

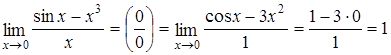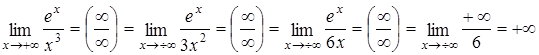Вывод: показательная функция (y=aⁿ) всегда растет быстрее, чем степенная (у=xⁿ).

.

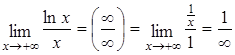Вывод: логарифмическая функция (y=log_ax) растет медленнее, чем степенная.

2. Неопределенность вида (0×¥) нужно преобразовать в неопределенность вида 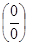или 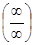, опустив один из множителей в знаменатель в отрицательной степени, и потом применять правило Лопиталя.

3. При показательной неопределенности: (0⁰), (1^¥), (¥⁰); прежде чем применять правило Лопиталя, нужно прологарифмировать этот предел по основанию e.

.

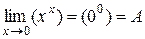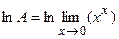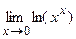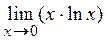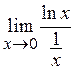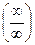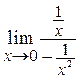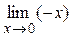= = =(0×¥)= = = =

= =0;

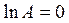Þ A=e⁰=1.

Формулы Тейлора и Маклорена.

Теорема. Пусть функция 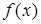n раз дифференцируема в окрестности точки x₀. Тогда в этой окрестности для функции 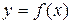справедлива следующая формула Тейлора:

+

+ .

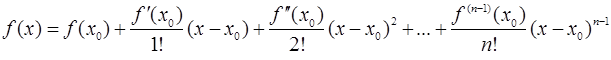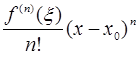Здесь 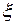некоторая точка, заключенная между 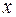и 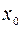( 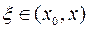), зависящая от 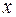, а 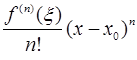= 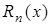- остаточный член в форме Лагранжа.

Если x₀=0, то формула Тейлора превращается в формулу Маклорена:

+

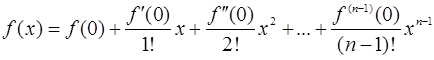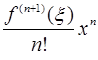
Признаки монотонности функции.

Пусть функция 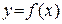определена и непрерывна на промежутке (a;b).

Определение: Функция 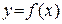называется неубывающей (невозрастающей) на (a;b), если для любых x₁<x₂, принадлежащих (a;b), выполняется ( ).

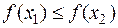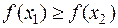Определение: Функция 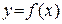называется возрастающей (убывающей) на (a;b), если для любых x₁<x₂, принадлежащих (a;b), выполняется ( ).

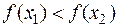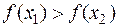Теорема 1.

Для того чтобы функция 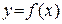, дифференцируемая на (a;b), была возрастающей, необходимо, чтобы производная на этом промежутке была неотрицательна, т.е. 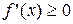, и достаточно, чтобы .

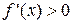Теорема 2.

Для того чтобы функция 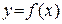, дифференцируемая на (a;b), была убывающей, необходимо, чтобы производная на этом промежутке 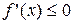и достаточно, чтобы .

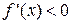Пример: Найти интервалы возрастания и убывания функции .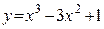

.

.

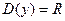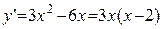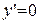Þ .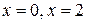

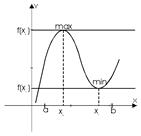Экстремум функции.

Пусть функция 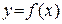определена в окрестности точки x₀.

Определение: Точка x₀ называется точкой строгого локального максимума, если существует такая ее окрестность точки, в которой выполняется неравенство .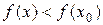

x₀ — max.

Определение: Точка x₀ называется точкой строгого локального минимума, если существует такая ее окрестность точки, в которой выполняется неравенство .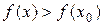

x₀ — min.

Точки локального максимума и минимума называются точками экстремума.

Необходимое условие экстремума дифференцируемой функции.

Если функция 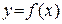, дифференцируемая в точке x₀, имеет в этой точке экстремум, то производная .

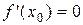Точки, в которых производная 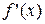либо равна 0, либо не существует, называются критическими точками производной.

Замечание 1: Обратное утверждение не верно. Не всякая функция, производная которой в точке равна нулю или не существует, имеет в этой точке экстремум.

Замечание 2. Функция имеет экстремум только в критических точках.

Таблица интегралов.

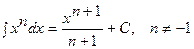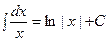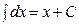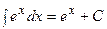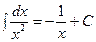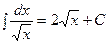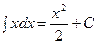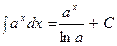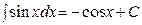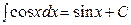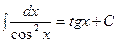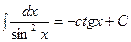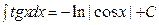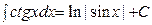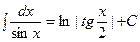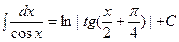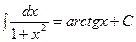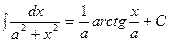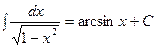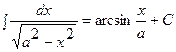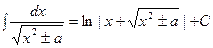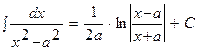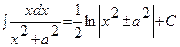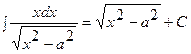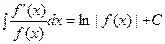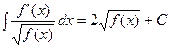Й случай.

Интеграл 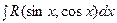универсальной тригонометрической подстановкой 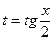сводится к интегралу от рациональной функции. При этом .

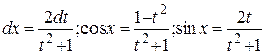С учетом сделанной замены получим

,

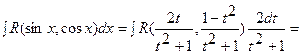
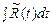где 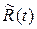- рациональная функция, интеграл от которой рассматривался выше.

Пример: Найти неопределенный интеграл: .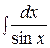

Решение: Сделаем универсальную тригонометрическую подстановку:

; .

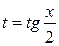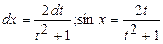Тогда .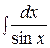

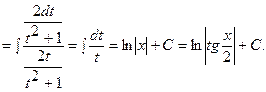Отметим, что универсальную тригонометрическую подстановку, как правило, используют в тех случаях, когда другие подстановки, приведенные ниже не приводят к желаемым результатам.

Й случай.

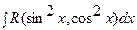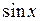В интегралах , где и 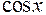входят в подынтегральную рациональную функцию, только в четных степенях делается замена 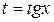. При этом

.

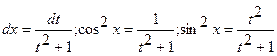Этой же подстановкой к интегралам от рациональных функций приводятся интегралы вида .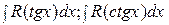

Пример: Найти неопределенный интеграл:

.

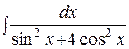Решение: Сделаем подстановку:

; .

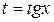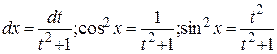Тогда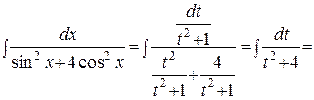

.

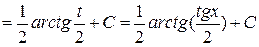3-й случай. Интегрирование выражений вида

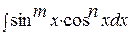, (6)

где mи n-целые числа. Рассмотрим два случая:

а) Среди чисел m,nесть хотя бы одно нечетное. Тогда за tпринимается функция, стоящая в основании другой степени.

Пример. Найти неопределенный интеграл:

.

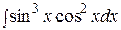Решение: Здесь функция 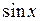стоит в нечетной степени, поэтому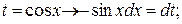

;

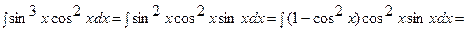
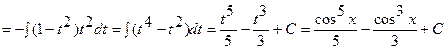б) В выражении (6) оба числаm,n- четные неотрицательные.

Положим m=2p, n=2q и применим формулы:

.

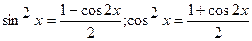Тогда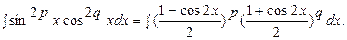

Раскрыв скобки, получим сумму интегралов, к каждому из которых применим 1-й или 2-й способы:

.

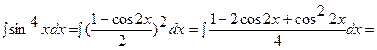
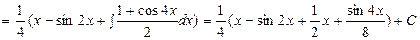Определенный интеграл.

Формула Ньютона-Лейбница.

,

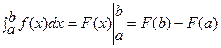где F(x)-одна из первообразных f(x).

Пример:

.

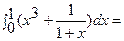
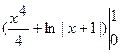
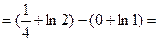
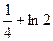Полярная система координат.

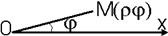Рассмотрим на плоскости точкуО, которую называют полюсом, и луч, выходящий из этой точки, который называется полярной осью.

Зададим на полярной оси масштаб. Каждой точке M поставим в соответствие два числа r - длина радиус-вектора 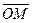и j - угол между радиус-вектором точки M и положительным направлением полярной оси.

Таким образом, любая точка в полярной системе координат будет иметь две координаты M(r,j), r – полярный радиус, j – полярный угол. Очевидно, что r – величина неотрицательная (как длина любого вектора), а угол может выбираться по договоренности (для однозначности определения координат) из промежутков 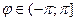или .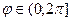

Если угол j откладывается от полярной оси против хода часовой стрелки, то его будем считать положительным, если по часовой стрелке, то отрицательным.

Изображение линий в полярной системе координат.

r= R – окружность с центром в полюсе и радиусом R.

j= a - луч под углом 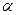к полярной оси.

r= j – при построении любой кривой в полярной системе координат, нужно задавать различные значения полярного угла j и вычислять соответственно значения полярного радиуса r. Если r получится меньше нуля, то картинки не будет (этой части рисунка не будет)

Спираль Архимеда	Кардиоида	3-х лепестковая роза		Лемниската Бернулли
r=j	r=1+cosj	r=cos3j	r=4cosj	r2=cos2j

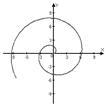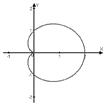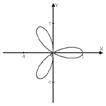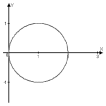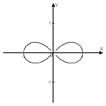Связь между декартовой и полярной системами координат.

Если полярную и декартову систему координат совместить так, чтобы полюс совпал с началом координат, а полярная ось с положительным направлением оси 0x, то можно получить формулы перехода от полярных координат (r;j ) к декартовым (x;y):

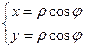, и от декартовых к полярным: ,

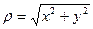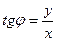
Объем тела вращения.

Определение: Если криволинейная трапеция ограничена линиями y=0; x=a; x=b; y=f(x), где f(x)³0вращается вокруг оси OX, то полученное тело называется телом вращения вокруг оси OX.

Как известно, объем тела выражается через площадь поперечного сечения по формуле: 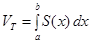. В данном случае поперечными сечениями являются круги радиусом R_кр=f(x); S_кр=S(x) = pf²(x) ÞV_OX= .

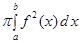Если фигура, ограниченная кривыми y₁=f₁(x) и y₂=f₂(x) [0 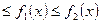] и прямыми x=a, x=b, вращается вокруг оси Ох, то объем тела вращения

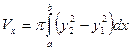
Если криволинейная трапеция ограниченная линиями 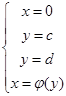вращается вокруг оси OY, то объем полученного тела вращения V_OY= .

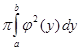Пример: Вычислить объем тела вращения, ограниченного линиями y=0; x=0; x=1; y=e^x.

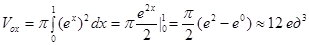
Теоремы о дифференцируемых функциях.

Теорема Ферма.

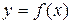Пусть функция определена и дифференцируема

на интервале (a;b) и в некоторой точке x₀ этого интервала принимает наибольшее или наименьшее значение. Тогда .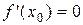

Геометрический смысл теоремы Ферма:

Так как 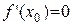, то угловой коэффициент касательной равен нулю 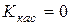Þ касательная параллельна оси ОХ.

Теорема Ролля.

Пусть функция 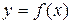определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), причем на концах интервала принимает одинаковые значения 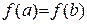. Тогда существует точка сÎ(a;b), значения производной в которой равно 0, т.е. .

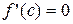Геометрический смысл теоремы Ролля:

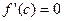Þ К_кас=0 Þ касательная

в точке c параллельна оси ОX.

Теорема Лагранжа.

Пусть функция 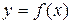определена и непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b). Тогда существует точка cÎ(a;b), значение производной в которой равно .

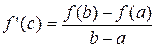Геометрический смысл теоремы Лагранжа:

.

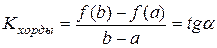Существует точка cÎ(a;b), в которой угловой коэффициент касательной равен угловому коэффициенту хорды, соединяющей граничные точки:

.

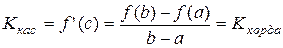Найдется такая точка на графике, касательная в которой параллельна хорде, стягивающей концы отрезка [a;b].

Теорема Коши.

Пусть функции f(x) и g(x) определены и непрерывны на отрезке [a;b] и дифференцируемы на интервале (a;b), причем производная функции g(x) отлична от нуля, g¢(x)¹0. Тогда существует такая точка cÎ(a;b), для которой выполняется равенство: .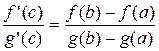

Правило Лопиталя.

Теорема.

Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки x₀, за исключением может быть самой точки x₀, и 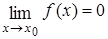, 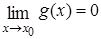. Тогда если существует предел отношения производных функций 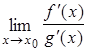, то существует предел отношения самих функций 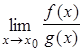, причем они равны между собой, т.е. .

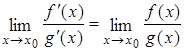В дальнейшем это утверждение будем также называть правилом Лопиталя

Замечание. На практике при раскрытии неопределенности типа 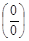можно пользоваться правилом Лопиталя и в случаях, когда x®±¥, x®¥.

Для раскрытия неопределенностей типа 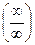существует аналог правила Лопиталя.

Замечание 1. Правилом Лопиталя можно пользоваться при раскрытии неопределенностей вида (¥-¥), (0×¥), (1^¥), (¥⁰), (0⁰), сводя их к неопределенностям типа , .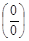

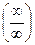Замечание 2. Если после применения правила Лопиталя опять получаем неопределенность вида 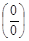или 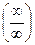, то его можно применить повторно.

Пример: Вычислить пределы по правилу Лопиталя.

1. Чтобы применять правило Лопиталя при неопределенности вида 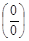или 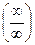, нужно продифференцировать отдельно числитель и знаменатель дроби, и вычислить полученный предел.

.

.

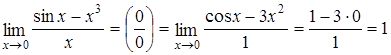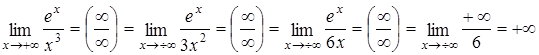Вывод: показательная функция (y=aⁿ) всегда растет быстрее, чем степенная (у=xⁿ).

.

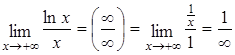Вывод: логарифмическая функция (y=log_ax) растет медленнее, чем степенная.

2. Неопределенность вида (0×¥) нужно преобразовать в неопределенность вида 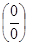или 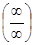, опустив один из множителей в знаменатель в отрицательной степени, и потом применять правило Лопиталя.

3. При показательной неопределенности: (0⁰), (1^¥), (¥⁰); прежде чем применять правило Лопиталя, нужно прологарифмировать этот предел по основанию e.

.

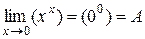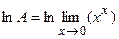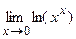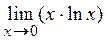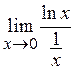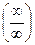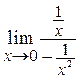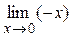= = =(0×¥)= = = =

= =0;

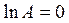Þ A=e⁰=1.

Формулы Тейлора и Маклорена.

Теорема. Пусть функция 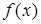n раз дифференцируема в окрестности точки x₀. Тогда в этой окрестности для функции 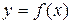справедлива следующая формула Тейлора:

+

+ .

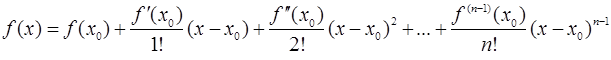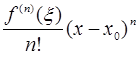Здесь 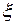некоторая точка, заключенная между 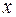и 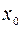( 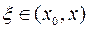), зависящая от 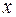, а 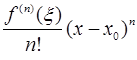= 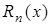- остаточный член в форме Лагранжа.

Если x₀=0, то формула Тейлора превращается в формулу Маклорена:

+

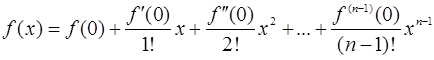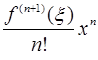
Признаки монотонности функции.

Пусть функция 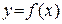определена и непрерывна на промежутке (a;b).

Определение: Функция 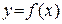называется неубывающей (невозрастающей) на (a;b), если для любых x₁<x₂, принадлежащих (a;b), выполняется ( ).

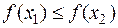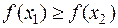Определение: Функция 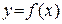называется возрастающей (убывающей) на (a;b), если для любых x₁<x₂, принадлежащих (a;b), выполняется ( ).

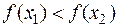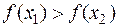Теорема 1.

Для того чтобы функция 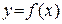, дифференцируемая на (a;b), была возрастающей, необходимо, чтобы производная на этом промежутке была неотрицательна, т.е. 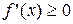, и достаточно, чтобы .

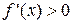Теорема 2.

Для того чтобы функция 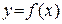, дифференцируемая на (a;b), была убывающей, необходимо, чтобы производная на этом промежутке 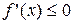и достаточно, чтобы .

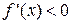Пример: Найти интервалы возрастания и убывания функции .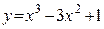

.

.

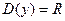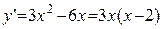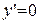Þ .

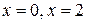Экстремум функции.

Пусть функция 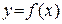определена в окрестности точки x₀.

Определение: Точка x₀ называется точкой строгого локального максимума, если существует такая ее окрестность точки, в которой выполняется неравенство .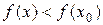

x₀ — max.

Определение: Точка x₀ называется точкой строгого локального минимума, если существует такая ее окрестность точки, в которой выполняется неравенство .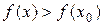

x₀ — min.

Точки локального максимума и минимума называются точками экстремума.

Необходимое условие экстремума дифференцируемой функции.

Если функция 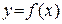, дифференцируемая в точке x₀, имеет в этой точке экстремум, то производная .

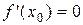Точки, в которых производная 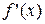либо равна 0, либо не существует, называются критическими точками производной.

Замечание 1: Обратное утверждение не верно. Не всякая функция, производная которой в точке равна нулю или не существует, имеет в этой точке экстремум.

Замечание 2. Функция имеет экстремум только в критических точках.