Выбор и определение числа неизвестных

Идею метода перемещений рассмотрим на примере. Пусть требуется рассчитать раму, изображенную на рис.17.1,а.

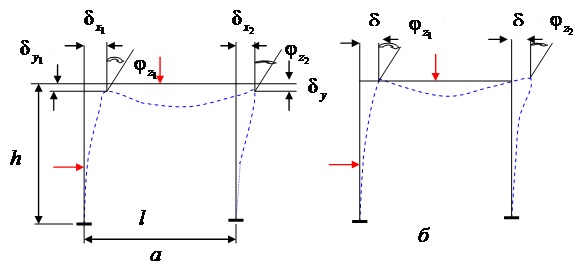
Рис.17.1. К определению числа неизвестных метода перемещений: а – учитываютсяпродольные деформации стержней, б - продольные деформации стержней не учитываются

В результате деформации рамы под нагрузкой ее узлы смещаются в новое положение, приобретая при этом перемещения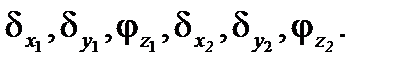

Если бы удалось каким-либо образом найти эти перемещения, то дальнейший расчет свелся бы к расчету каждого стержня в отдельности как статически неопределимой балки на действие заданных нагрузок и узловых перемещений. При этом можно было бы пользоваться приведенной в разделе 4 лекции 16 таблицей 16.1. Метод расчета, в котором узловые перемещения рассматриваются как основные неизвестные, называется методом перемещений.

Сущность метода рассмотрим, упростив задачу, а именно: пренебрежем деформациями растяжения-сжатия. Тогда деформированное состояние будет таким, как показано на рис.17.1,б. При этом узлы смещаются по горизонтали за счет изгиба стоек на одно и то же расстояние d, узел 1 рамы поворачивается на угол 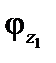, а узел 2 — на угол 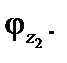Число неизвестных при этом уменьшается до трех.

В общем случае число неизвестных метода перемещений n следует определять по формуле:

(17.1)

где n_у— число неизвестных углов поворота,

n_л — число неизвестных линейных перемещений узлов.

Число неизвестных углов поворота для плоских конструкций в точности равно числу жестких узлов рамы. При этом жесткими называются такие узлы, в которых жестко соединяются между собой по крайней мере два стержня конструкции. Примеры жестких узлов показаны на рис.17.2.

Рис.17.2.Примеры жестких узлов

Число неизвестных линейных узловых перемещений в упрощенном варианте расчета (без учета продольных деформаций стержней) подсчитывается следующим образом.

Предполагается, что расстояния между концами стержней вследствие изгиба изменяются незначительно и этими изменениями можно пренебречь. Это дает основание при подсчете числа независимых линейных перемещений узлов перейти к анализу шарнирно-стержневой системы, полученной из заданной конструкции постановкой полных шарниров во все узлы, включая опорные. Если в такой системе возможны перемещения узлов без деформаций удлинения или укорочения стержней, то они возможны и в заданной конструкции. Следовательно, число независимых линейных перемещений равно степени геометрической изменяемости шарнирно-стержневой системы, полученной описанным выше способом. Эта характеристика подсчитывается по формуле:

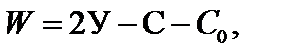
где У - число узлов шарнирно-стержневой схемы, включая опорные,

С - число стержней конструкции,

С₀ - число опорных стержней.

Вычислим по формуле (17.1), в качестве примера, число неизвестных метода перемещений для рамы рис.17.1. Рама имеет два жестких узла, следовательно, n_у=2. Введем шарниры во все узлы рамы, как показано на рис.17.3.

Рис.17.3. Шарнирно-стержневая модель рассчитываемой рамы

Учитывая, что число стержней конструкции равно трем, а число опорных стержней — четырем (каждая шарнирно-неподвижная опора эквивалентна двум опорным стержням), находим:

n_л = W = 2У-С-С₀= 2×4 - 3 - 4 = 1.

Таким образом, 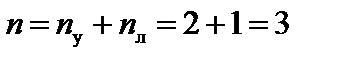.