Расчет симметричных рам на действие симметричных и обратно симметричных нагрузок
Симметричная конструкция— это такая конструкция, которая имеет симметрию в расположении и в жесткостях элементов.
Расчет симметричных рам можно существенно упростить за счет разделения основных неизвестных на две группы: прямо и обратно симметричные. Методику упрощения рассмотрим на примере.
Пусть надо рассчитать симметричную конструкцию, изображенную на рис.16.1, а. Данная конструкция трижды статически неопределима.
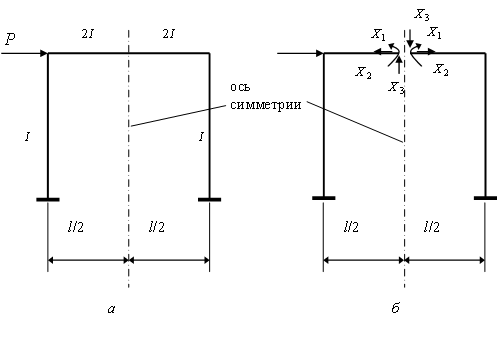
Ри.16.1. Симметричная рама (а) и ее симметричная основная система (б)
При расчете данной конструкции обычным способом пришлось бы составлять и решать систему из 3 совместных уравнений с 3 неизвестными:
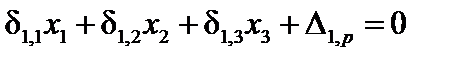
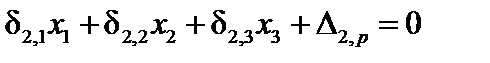
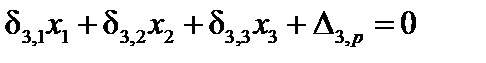
Однако решение можно упростить, если выбрать симметричную основную систему, как показано на рис.16.1,б. Такой выбор системы приводит к тому, что единичные эпюры 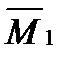 и
и 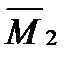 оказываютсяпрямо симметричными, а единичная эпюра
оказываютсяпрямо симметричными, а единичная эпюра 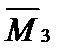 — обратно симметричной (рис.16.2). Грузовая эпюра при нагрузке, показанной на рис.16.1,а, в данном случае является несимметричной (рис.16.3).
— обратно симметричной (рис.16.2). Грузовая эпюра при нагрузке, показанной на рис.16.1,а, в данном случае является несимметричной (рис.16.3).
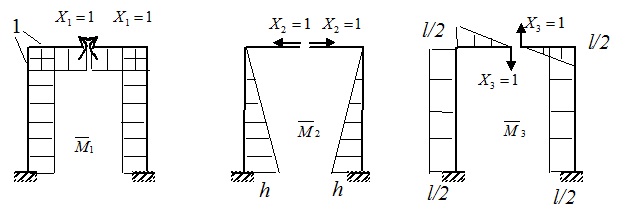
Рис.16.2.Единичные эпюры моментов при основной системе, показанной на рис.16.1,а
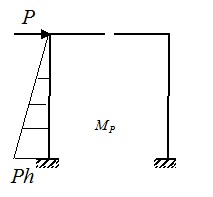
Рис.16.3.Грузовая эпюра моментов при основной системе, показанной на рис.16.1,а
Коэффициенты канонических уравнений, которые находятся перемножением прямо и обратно симметричных эпюр, обратятся в ноль. При этом:
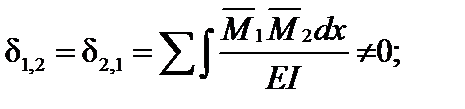
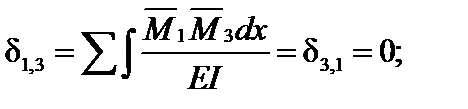
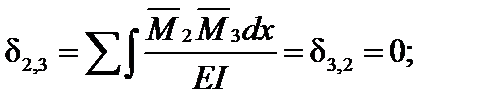 ;
; 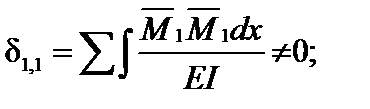 ;
;
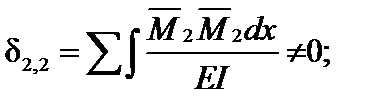
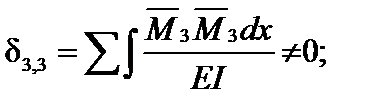 .
.
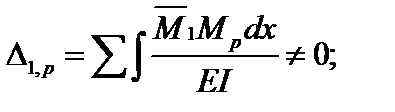
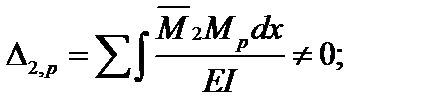
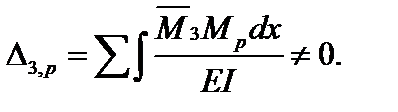
Система канонических уравнений принимает вид:
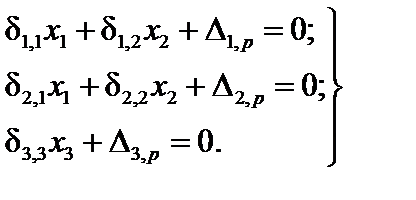 | (16.1) |
т.е. распадается на две подсистемы меньшего порядка. Расчет упрощается и за счет того, что единичные эпюры можно строить только для одной половины рамы и вычисление коэффициентов при неизвестных так же можно проводить только для одной половины, удваивая результат.
Если нагрузка при этом является прямо симметричной, как показано на рис.16.4,а, то коэффициент 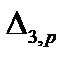 в системе уравнений (16.1) обращается в нуль, и из третьей строки этой системы получаем Х3=0.
в системе уравнений (16.1) обращается в нуль, и из третьей строки этой системы получаем Х3=0.
Вывод: при действии на симметричную конструкцию симметричной нагрузки обратно симметричные неизвестные всегда раны нулю. Это упрощает расчет симметричных рам.
Аналогично можно доказать, что при действии на симметричную раму обратно симметричной нагрузки прямо симметричные неизвестные равны нулю.
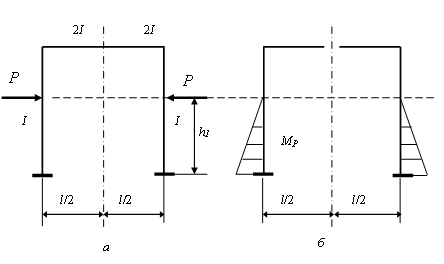
Рис.16.4.Симметрично нагруженная рама (а) и симметричная грузовая эпюра моментов для основной системы (б)
Если рама имеет несколько пролетов, то даже при выборе симметричной основной системы не всегда удается сразу получить прямо и обратно симметричные неизвестные.
Рассмотрим, например, раму, изображенную на рис.16.5, а. Данная конструкция симметрична. Для нее можно выбрать симметричную основную систему (рис.16.5,б), но основные неизвестные при этом оказываются несимметричными, и никакого выигрыша при использовании основной системы рис.16.5,б получить невозможно.В таких случаях полезен способ группировки неизвестных, который заключается в следующем:
а б
Рис.16.5. Симметричная рама (а) с симметричной основной системой и несимметричными основными неизвестными (б)
Представим основные неизвестные 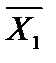 и
и 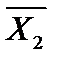 в виде:
в виде:
|
Приложим силы 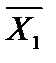 и
и 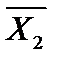 , определяемые формулами (16.2), к основной системе рис. 16.6, б, как показано на рис. 16.6, а, затем разобьем их на две группы, показанные на рис. 16.6, б и в.
, определяемые формулами (16.2), к основной системе рис. 16.6, б, как показано на рис. 16.6, а, затем разобьем их на две группы, показанные на рис. 16.6, б и в.
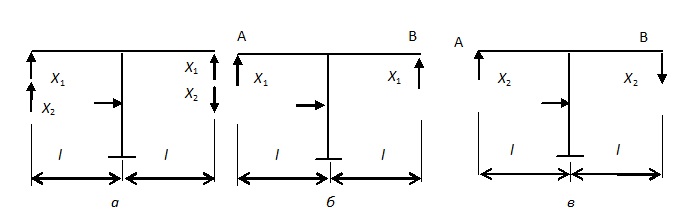
Рис.16.6. Групповые неизвестные:
а - сумма групповых неизвестных, б – первая групповая неизвестная, в – вторая групповая неизвестная
Две силы Х1 приложенные в точках А и В, назовем первой групповой неизвестной, а две силы Х2 в тех же точках— второй групповой неизвестной. Первая групповая неизвестная является прямо симметричной, а вторая — обратно симметричной, при этом побочные коэффициенты 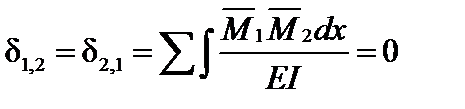 , за счет чего достигается упрощение решения задачи.
, за счет чего достигается упрощение решения задачи.
ПРЕОБРАЗОВАНИЕ ПРОИЗВОЛЬНОЙ НАГРУЗКИ К ПРЯМО И ОБРАТНО СИММЕТРИЧНОМУ ВИДУ
Допустим, что на симметричную конструкцию действует несимметричная нагрузка, например, силаР, приложенная в произвольной точке А (рис. 16.7). Найдем на правой половине рамы симметрично расположенную точку 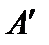 и приложим в этой точке две противоположно направленные силы, равные Р/2 каждая. Силу Р в точке А представим также состоящей из двух частей, равных Р/2.
и приложим в этой точке две противоположно направленные силы, равные Р/2 каждая. Силу Р в точке А представим также состоящей из двух частей, равных Р/2.
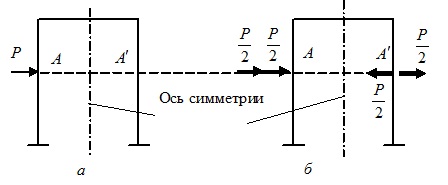
Рис.16.7. Замена несимметричной нагрузки (а) суммой прямо и обратно симметричных нагрузок (б)
Очевидно, что нагрузки, показанные на рис.16.7,а и б, эквивалентны между собой. Очевидно также, что нагрузку, показанную на рис.16.7,б можно представить в виде суммы двух, как показано на рис.16.8.
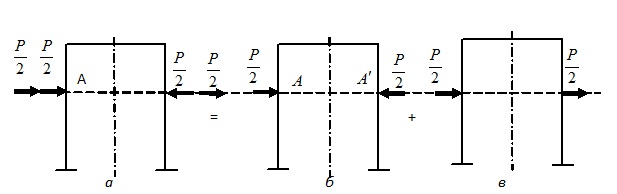
а б в
Рис.16.8. Преобразование нагрузки: а – суммарная нагрузка, б – прямо симметричная нагрузка, в – обратно симметричная нагрузка.
Но нагрузка на рис.16.8,б является прямо симметричной, а нагрузка на рис.16.8, в— обратно симметричной. Таким образом, произвольную нагрузку можно представить как сумму двух, одна из которых является прямо, а другая — обратно симметричной.