Линии влияния для простой балки

Рассмотрим балку на двух опорах с консолями и установим на ней движущийся груз Р=1 (см.рис.10.1,а). Текущее положение груза зададим координатой х, которую будем отсчитывать от левой опоры. Составим уравнение равновесия всех сил в виде суммы моментов относительно точки В. Получим:

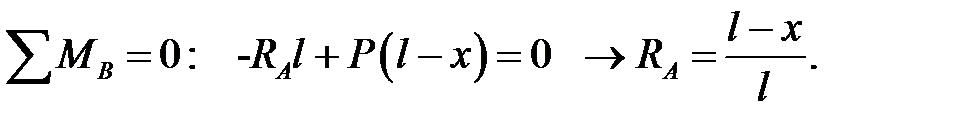(10.1)

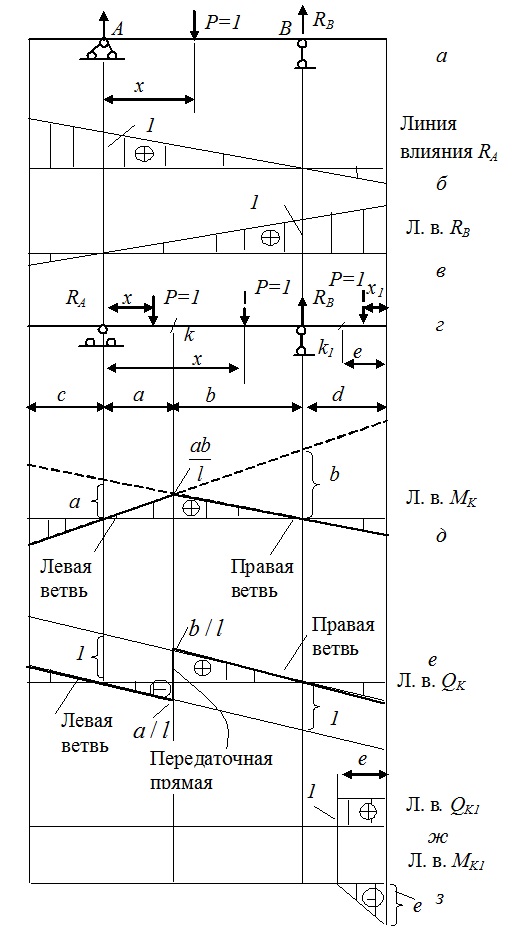
Рис.10.1. Построение линий влияния для балки

Формула (10.1) описывает закон изменения опорной реакции 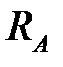при движении единичного груза. Из формулы видно, что эта реакция изменяется по линейному закону. График функции (10.1) представлен на рис.10.1,б. Он легко строится по двум точкам: 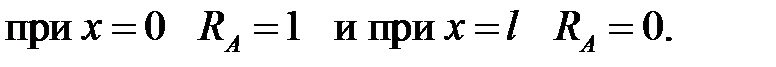Остальные ординаты этого графика легко найти по линейной интерполяции.

Это и есть линия влияния опорной реакции .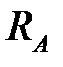

Чтобы получить уравнение линии влияния опорной реакции 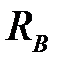, составим уравнение равновесия в виде суммы моментов относительно точки А:

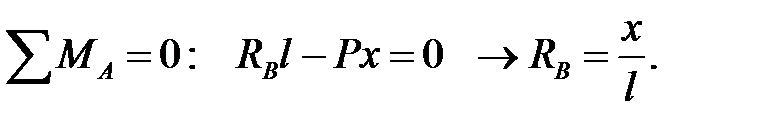(10.2)

Формула (10.2) есть уравнение линии влияния опорной реакции R_B. По этому уравнению строим линию влияния R_B (рис.10.1,в).

В соответствии с изложенным выше, сформулируем правила построения линий влияния опорных реакций, чтобы в дальнейшем не составлять никаких уравнений.

Правило 1: Чтобы построить линию влияния опорной реакции R_A необходимо отложить на опоре А ординату, равную 1, на опоре В — ординату, равную нулю, и соединить вершины ординат прямой линией. При наличии консолей эту линию необходимо продлить до конца консолей.

Правило 2: Чтобы построить линию влияния опорной реакции R_B необходимо отложить на опоре В ординату, равную 1, на опоре А — ординату, равную нулю, и соединить вершины ординат прямой линией. При наличии консолей эту линию необходимо продлить до конца консолей.

Построим линию влияния изгибающего момента в пролетном сечении к. Расположим груз Р=1 левее сечения к . При таком положении груза изгибающий момент в сечении к проще найти через опорную реакцию R_B. Получаем:

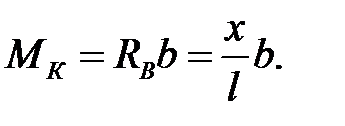(10.3)

Формула (10.3) дает закон изменения изгибающего момента в сечении к, когда груз Р = 1 при его движении по балке находится в точке к или левее этой точки. Поэтому формула (10.3) представляет уравнение левой ветви линии влияния M_K. Из формулы (10.3) видно, что левая ветвь линии влияния M_K совпадает с линией влияния опорной реакции R_B, все ординаты которой увеличены в 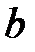раз.

Из формулы (10.3) при х=а находим ординату линии влияния в точке к:

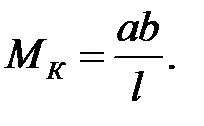
Чтобы построить левую ветвь, нужно взять за основу линию влияния R_B , ординаты которой увеличены в 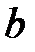раз, и обвести жирной линией ту ее часть, которая находится левее точки к(см.рис.10.1,д).

Расположим теперь груз Р=1 правее сечения к.На рис.10.1,г с это положение показано пунктиром. При таком положении груза изгибающий момент в сечении к проще найти через опорную реакцию R_A.Получаем:

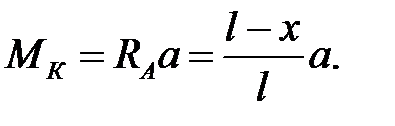(10.4)

Формула (10.4) дает уравнение правой ветви линии влияния M_K. Из этой формулы видно, что правая ветвь линии влияния M_K совпадает с линией влияния опорной реакции R_A, все ординаты которой увеличены в a раз. При х=а получаем:

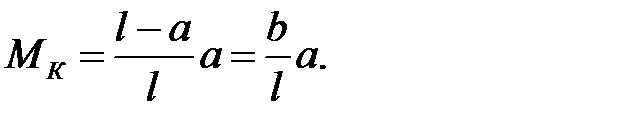
Таким образом, левая и правая ветви в точке к имеют одну и ту же ординату, т.е.они пересекаются в этой точке.

В окончательном виде линия влияния M_K представлена на рис.10.1,д.

Из изложенного можно сформулировать следующее правило построения линии влияния изгибающего момента в пролетном сечении к, расположенном на расстоянии а от левой опоры и на расстоянии b от правой.

Правило 3: Чтобы построить линию влияния изгибающего момента для сечения, расположенного на расстоянии а от левой опоры и на расстоянии b от правой, необходимо взять за основу линию влияния правой опорной реакции, увеличенную в b раз, часть этой линии левее точки к принять в качестве левойветви линии влияния изгибающего момента; на линию влияния опорной реакции спроецировать сечение к, через вершину полученной ординаты и нулевую точку на правой опоре провести прямую линию до конца правой консоли и принять полученную прямую в качестве правой ветви линии влияния изгибающего момента.

Построим линию влияния поперечной силы для пролетного сечения к. Следуя методике, принятой при построении линии влияния изгибающего момента, расположим груз Р=1 поочередно слева и справа от рассматриваемого сечения и для каждого положения груза получим формулу для поперечной силы.

Груз Р=1 слева от сечения. При таком положении груза поперечная сила в сечении к равна Q_K = - R_B. Это означает, что левая ветвь линии влияния поперечной силы совпадает с линией влияния правой опорной реакции, взятой со знаком минус.

Груз Р=1 справа от сечения. При таком положении груза поперечная сила в сечении к равна Q_K = R_A. Это означает, что правая ветвь линии влияния поперечной силы совпадает с линией влияния левой опорной реакции.

В сечении к проходит передаточная прямая (см.рис.10.1,е).

Правило 4: Чтобы построить линию влияния поперечной силы для сечения, расположенного на расстоянии а от левой опоры и на расстоянии b от правой, необходимо взять за основу линию влияния правой опорной реакции со знаком минус и линию влияния левой опорной реакции со знаком плюс; спроецировать на эти линии сечение к; в качестве окончательного результата принять часть линии влияния правой опорной реакции слева от сечения к и часть линии влияния левой опорной реакции справа от сечения к.

В заключение данного раздела рассмотрим построение линий влияния изгибающего момента и поперечной силы для консольного сечения к₁.

Заметим, что при положении груза Р=1 слева от сечения к₁ изгибающий момент и поперечная сила в этом сечении будут равны нулю. При положении груза правее сечения эти величины могут быть найдены по формулам:

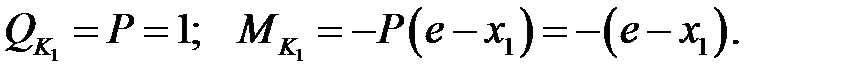(10.5)

По формулам (10.5) строим линии влияния 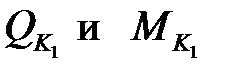(см.рис.10,1, ж,з).