Метод Ньютона (метод касательных)
Рассмотренные ранее методы решения нелинейных уравнений являются методами прямого поиска. В них для нахождения корня используется нахождение значения функции в различных точках интервала [a,b].
Метод Ньютона относится к градиентным методам, в которых для нахождения корня используется значение производной.
Дано нелинейное уравнение: f(x)=0
Найти корень на интервале [a,b] с точностью ɛ.
Метод Ньютона основан на замене исходной функции f(x), на каждом шаге поиска касательной, проведенной к этой функции. Пересечение касательной с осью Х дает приближение корня (Рисунок 6).
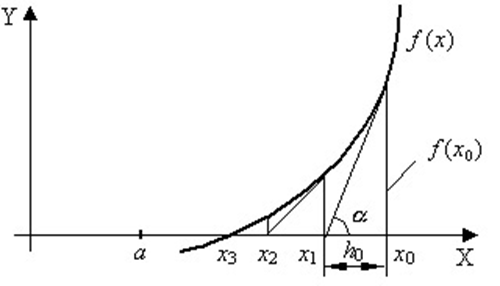
Выберем начальную точку x0=b (конец интервала изоляции). Находим значение функции в этой точке и проводим к ней касательную, пересечение которой с осью Х дает нам первое приближение корня x1.
Рисунок 6 – Геометрический смысл метода
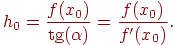x1 = x0 – h0,где
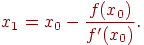
Поэтому
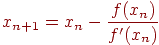В результате итерационный процесс схождения к корню реализуется рекуррентной формулой (4.6)
Процесс поиска продолжаем до тех пор, пока не выполнится условие:
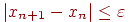 | (4.7) |
Упростим условие (4.7), исходя из (4.6). Получим:
 | (4.8) |
Метод обеспечивает быструю сходимость, если выполняется условие:
 | (4.9) |
т.е. первую касательную рекомендуется проводить в той точке интервала [a,b], где знаки функции f(x0) и ее кривизны f"(x0) совпадают.
Модифицированный метод ньютона (метод секущих)
В этом методе для вычисления производных на каждом шаге поиска используется численное дифференцирование по формуле:
Тогда рекуррентная формула (4.6) будет иметь вид:
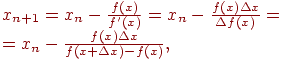 | (4.10) |
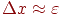где
Метод хорд
Метод основан на замене функции f(x) на каждом шаге поиска хордой, пересечение которой с осью Х дает приближение корня.
При этом в процессе поиска семейство хорд может строиться:
а) при фиксированном левом конце хорд, т.е. z=a, тогда начальная точка х0=b (Рисунок 7а);
б) при фиксированном правом конце хорд, т.е. z=b, тогда начальная точка х0=a (Рисунок 7б);
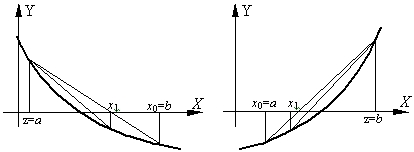
Рисунок 7а,б - Геометрический смысл метода
В результате итерационный процесс схождения к корню реализуется рекуррентной формулой:
для случая а)
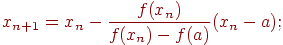 | (4.11) |
для случая б)
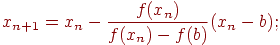 | (4.12) |
Процесс поиска продолжается до тех пор, пока не выполнится условие:
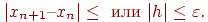 | (4.13) |
Метод обеспечивает быструю сходимость, если f(z)f"(z) > 0, т.е. хорды фиксируются в том конце интервала [a,b], где знаки функции f(z) и ее кривизны f"(z) совпадают.
Алгоритмическое конструирование
Пояснение задачи
Реализовать программу для решения нелинейных уравнений.
Методами:
1. Половинного деления.
2. Простых итераций.
3. Ньютона (метод касательных).
4. Хорд.
С помощью программной среды Pascal ABC.NET.
В качестве проверки работоспособности программы решить уравнения:
x4-3x+1=0
lgx=10-x
Выявить самый быстрый и действенный метод решения.
Для выполнения задания функция x4-3x+1=0 была протабулирована с шагом 0,2 на отрезке [0.1;4].
| X | Y |
| 0.1 | 0.7001 |
| 0.3 | 0.1081 |
| 0.5 | -0.4375 |
| 0.7 | -0.8599 |
| 0.9 | -1.0439 |
| 1.1 | -0.8359 |
| 1.3 | -0.0439 |
| 1.5 | 1.5625 |
| 1.7 | 4.2521 |
| 1.9 | 8.3321 |
| 2.1 | 14.1481 |
| 2.3 | 22.0841 |
| 2.5 | 32.5625 |
| 2.7 | 46.0441 |
| 2.9 | 63.0281 |
| 3.1 | 84.0521 |
| 3.3 | 109.6921 |
| 3.5 | 140.5625 |
| 3.7 | 177.3161 |
| 3.9 | 220.6441 |
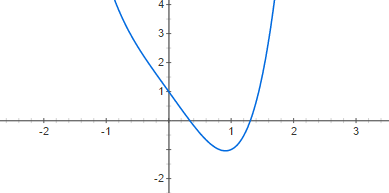
Рис. 8 - График функции x4-3x+1=0 .
Для выполнения задания функция lgx=10-x была протабулирована c шагом 0,2 на отрезке [0.1;4].
| X | Y |
| 0.1 | -1.7943 |
| 0.3 | -1.0241 |
| 0.5 | -0.6173 |
| 0.7 | -0.3544 |
| 0.9 | -0.1717 |
| 1.1 | -0.0380 |
| 1.3 | 0.0638 |
| 1.5 | 0.1445 |
| 1.7 | 0.2105 |
| 1.9 | 0.2662 |
| 2.1 | 0.3143 |
| 2.3 | 0.3567 |
| 2.5 | 0.3948 |
| 2.7 | 0.4294 |
| 2.9 | 0.4611 |
| 3.1 | 0.4906 |
| 3.3 | 0.5180 |
| 3.5 | 0.5438 |
| 3.7 | 0.5680 |
| 3.9 | 0.5909 |
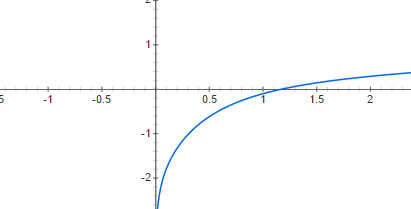
Рисунок 9 - График функции lgx=10-x.