Алгоритм нахождения производных и интегралов

I способ.Через меню символьных операций Symbolics:

Для того, чтобы найти производную или неопределенный интеграл с помощью меню, введите в рабочий документ выражение, которое необходимо продифференцировать или проинтегрировать и выделите аргумент в любом месте выражения. Далее щелкните по строке Differentiate (дифференцирование) илиIntegrate (интегрирование) в пункте Variabe(переменная)меню Symbolics.

II способ.С помощью пиктограммы Calculus(матанализ):

1. В панели Матанализнужновыбрать операцию, которую вы хотите выполнить.

2. При нажатии на соответствующий значок появляется шаблон с незаполненными полями (в виде черных квадратов).

3. Заполните пустые поля и нажмите c пиктограммы Symbolics.

Пример 1.Продифференцировать и проинтегрировать функцию . ►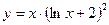

◄.

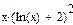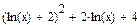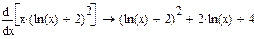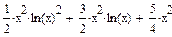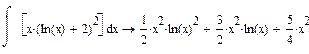Пример 2: Найти значение производной функции 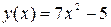в точке х:=0.37.

· Сначала введите точку, в которой будете находить производную, наберите х=0.37

· Щелкните ниже, затем нужно выбрать в панели Матанализзначок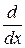

· В появившемся шаблоне щелкните в нижнем черном квадрате и наберите х, щелкните в поле справа и наберите выражение, которое нужно дифференцировать.

· Нажмите знак =, чтобы увидеть результат.

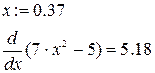
Для нахождения производных высших порядков используется символ 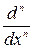и дополнительно заполняются два черных квадрата, где указывается порядок производной.

Пример 3. Найти производную 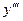для функции .►

◄

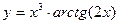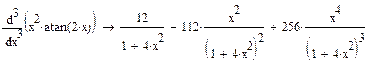Пример 4. Вычислить определенный интеграл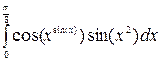

►Выберите в панели Матанализзначок определенного интеграла 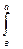. Появится шаблон интеграла с четырьмя полями для заполнения.

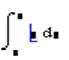
Заполните соответствующие поля и нажмите =.

◄

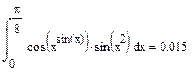Пример 5. Вычислить координаты центра масс треугольника, задаваемого неравенствами 0<x<1 и 0<y<x, плотность которого пропорционально расстоянию от начала координат. ►

· Вводим функцию .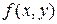

· Обозначим массу 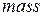, вводим имя массы. Нажимаем два раза на значок определенного интеграла, появится шаблон для заполнения.

· Заполняем шаблон и нажав = получим ,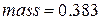

(для 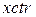и 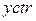−действия аналогичные).

◄

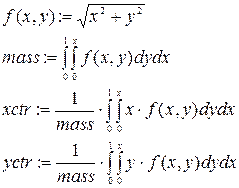
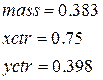Пример 6.Закон движения точки M в плоскости xy задан уравнениями

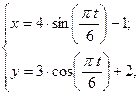(где x, y — в сантиметрах, t — в секундах).

Определить уравнение траектории точки; для момента времени 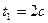, найти скорость и ускорение точки, а также ее касательное ускорение, нормальное ускорение и радиус кривизны в соответствующей точке траектории.

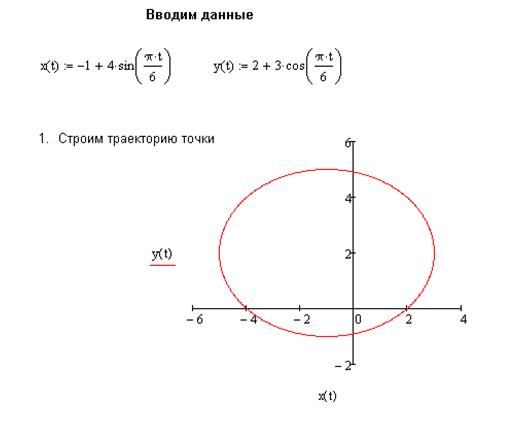
►Уравнение траектории точки будем искать в виде зависимости между координатами точки. Для исключения из уравнения движения времени t, которое входит в аргумент тригонометрических функций, используем формулу

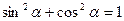или, считая 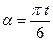, 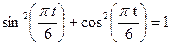. (12)

Из уравнений движения находим выражения тригонометрических функций

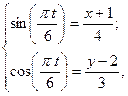
и подставляем их в равенство (12), получим

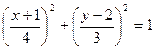. (13)

Таким образом, траекторией является эллипс, центр С которого имеет координаты (-1,2), а размеры полуосей, параллельных осям x и y, соответственно равны 4 см и 3 см.

Скорость точки найдем по ее проекциям на координатные оси:

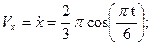
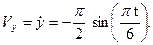
При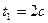

	;

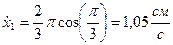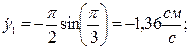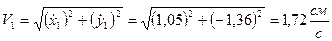При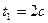

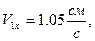
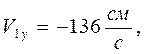
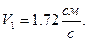
Теперь найдем ускорение точки:

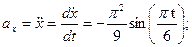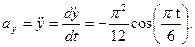При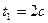

	.

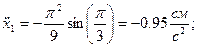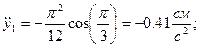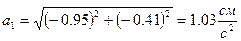При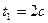

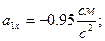
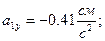
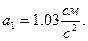
Так как движение точки задано координатным способом, то величины скорости и ускорения были определены по проекциям этих величин на координатные оси.

Теперь определим касательное и нормальное ускорения точки, то есть проекции вектора 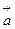на оси естественного трехгранника:

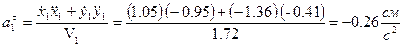Величина 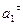является проекцией ускорения 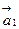на направление вектора 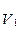. . 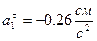Знак минус указывает на то, что вектор 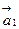противоположен вектору .

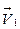Нормальное ускорение точки при известных значениях величин 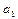и 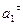вычисляется по формуле

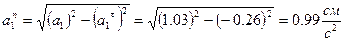Радиус кривизны траектории определим по формуле

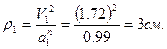
О т в е т: , , , , .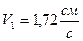

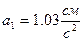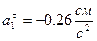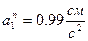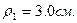Ниже приведен документ решения данной задачи в системе Mathcad

План выполнения работы

1. Выполните примеры 1 – 6, приведенные выше.

2. Найдите производную функции 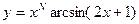и результат проверить интегрированием.

3. Проинтегрируйте функцию 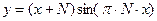и результат проверить дифференцированием.

4. Вычислите интегралы:

а) ;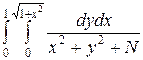

б) ;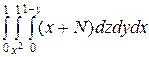

в) ;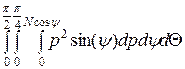

г)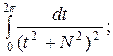

д) ;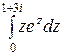

е) .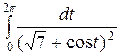

Контрольные вопросы

1. Как выполняется дифференцирование и интегрирование с помощью символьной переменной?

2. Каков порядок вычисления производных и интегралов?

Лабораторная работа №5

«Решение дифференциальных уравнений в Mathcad »

Цель работы: Познакомиться с методами решения дифференциальных уравнений.

I способ − аналитический

Можно решать уравнения с разделяющимися переменными интегрированием. Решение находится в виде функции.

Пример 1. Найти решение уравнения с разделенными переменными ydy=e^x/(e^x+1)dx, удовлетворяющее начальному условию y(0)=1 (задача Коши). Изобразите график решения (интегральную кривую, проходящую через точку (0,1)).

►1) Установите режим автоматических вычислений.

2) Установите режим отображения результатов символьных вычислений по горизонтали, установив метку Horizontaly в окне диалога строки Evaluation Style меню Symbolics.

3) Введите начальные условия y(x0)=y0:

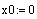
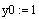
4) Если уравнение имеет вид Y(y)dy=X(x)dx, определите подынтегральные функции Y(y) и X(x):

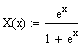
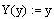
5) Вычислите с символьной переменной интегралы с переменными верхними пределами и нижними пределами, равными начальным условиям x0 и y0:

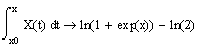
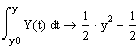
6) Запишите уравнение, задающее неявно y(x) как функцию x, и решите его относительно переменной y.

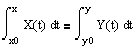
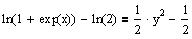
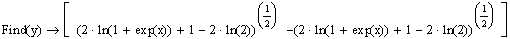
7) Выбираете решение, удовлетворяющее условию y(0)=1, и определите как функцию переменной x:

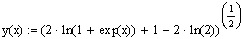
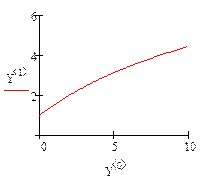
8) Постройте график найденного решения:

◄

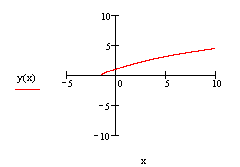II способ − численный

Аналитическое выражение для решений дифференциальных уравнений удается получить достаточно редко. Поэтому используются численные методы. Численное решение задачи Коши состоит в построении таблицы приближенных значений функции y(x), которая является решение, в узловых точках. Одним из численных методов решения задачи Коши является метод Рунге-Кутты. В системе Mathcad программа решения уравнений по методу Рунге-Кутты имеет имя rkfixed. Обращение к ней осуществляется через операцию присваивания какой-либо переменной имени программы с помощью встроенной функции

Z=rkfixed(y,x1,x2,n,f), где

y − вектор-столбец, задающий начальные условия;

x1 − левый конец отрезка интегрирования;

x2 − правый конец отрезка интегрирования;

n − число узлов на отрезке интегрирования;

f − имя вектора-функции f(x,y), содержащей правую часть уравнения.

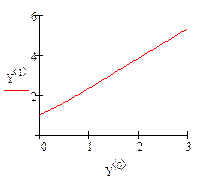
В результате будет получена матрица Z значений решения уравнения в узловых точках, по которым можно построить график функции, которая является решением уравнения.

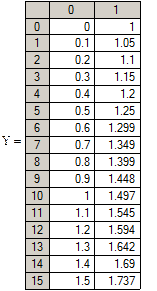
Ниже приведен фрагмент документа решения примера 1 методом Рунге-Кутты

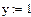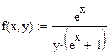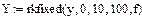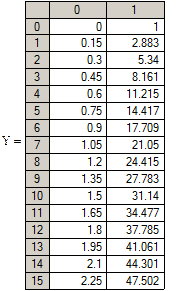
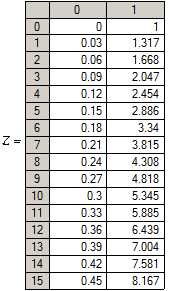
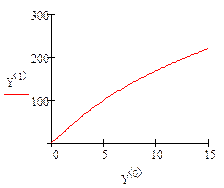
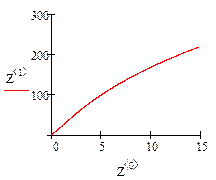
Пример 2.Решить задачу Коши 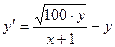, 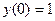методом Рунге-Кутты на промежутке 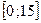из 100 и 500 узлов.

►

◄

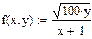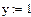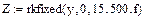Пример 3. Решите на отрезке [0,3] задачу Коши у"=ехр(-ху), у(0)=1, у'(0)=1 методом Рунге-Кутты с постоянным шагом на сетке из 100 равноотстоящих узлов.

►Сведем решение уравнения к решению системы. Обозначим у₀=у(х) и у₁=у'(х). Поскольку у"=(у')'=(y₁)', то получим

(у₀)'=y₁, y₀(0)=1.

(y₁)'=exp(-xy₀), y₁(0)=1, то начальные условия будут заданы в виде столбца .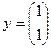

Уравнение будет эквивалентно системе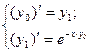

Правая часть уравнения вводится элементами вектора-столбца

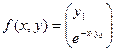
Ниже приведен фрагмент решение уравнения в Mathcad

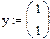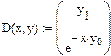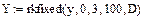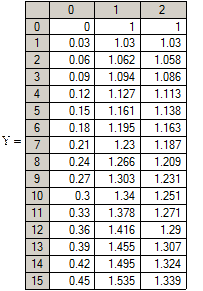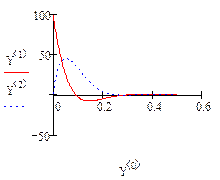
Пример 4.Решить систему уравнений состояния 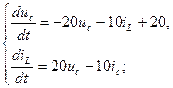при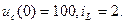

►Обозначим 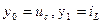и система примет вид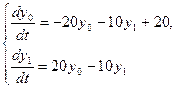

Ниже приведен фрагмент решение системы уравнений в Mathcad на промежутке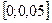

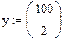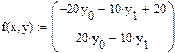Пример 5. Решить задачу Коши: 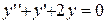, , 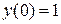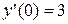на отрезке [0,0.5].

►Это уравнение можно представить в виде системы:

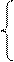
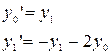
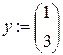- матрица-вектор начальных условий

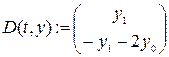- функция правых частей системы уравнений в виде матрицы-вектора относительно первых производных неизвестных функций.

◄

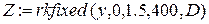
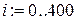
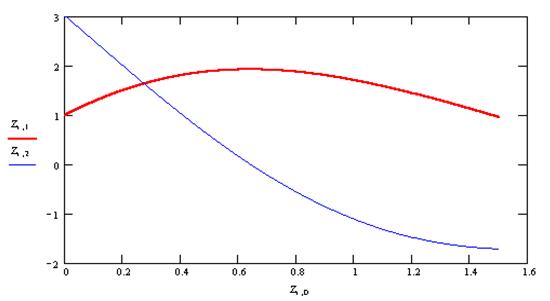Порядок выполнения работы

1. Выполните примеры 1 −5 из описания работы.

2. Решите уравнение 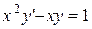при начальных условиях y(1)=0 в промежутке [1;2]с шагом h=0.2.

3. Решить уравнение y``+N y`+17y=x+N.

Контрольные вопросы

1.Опишите, в чем заключается метод Рунге-Кутта.

2.Какие функции применяются при решении дифференциальных уравнений в MathCAD?

Лабораторная работа №6

«Важнейшие математические преобразования в Mathcad »

Цель работы: научиться находить математические преобразования.

Преобразование Лапласа

Преобразование Лапласа в Mathcad выполняется в символьной форме, поэтому все выражения являются функциями: в области оригинала от времени t, в области изображения от комплексной переменной s.

Пример 1. Найти изображение функции f(t)= 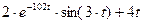и выполнить проверку.

►Отмечаем мышью переменную t (она будет окружена рамкой) в любом месте выражения. Затем, переходим в пункт меню Символы->Преобразование->Лапласа. Можно пользоваться пиктограммой Symbolics.Для того чтобы найти изображение функции, нужно щелкнуть по слову laplaseв панели Symbolics,заполнить черный квадратик переменной t и щелкнуть вне рамки.

◄

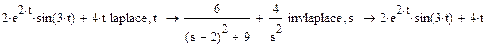Чтобы получить обратное преобразование Лапласа нужно проделать то же самое, что и в первом случае, только функция должна зависеть от комплексной переменной s. Соответствующий пункт меню находится ниже предыдущего Лапласа Обратное, а на пиктограмме Symbolicsнужно использовать слово invlaplase.

Пример 2. Найти оригинал по изображению f(s)= 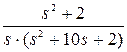и выполнить проверку.

►

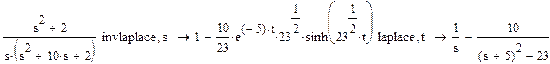Последнее выражение упрощаем, для этого в меню Symbolicsвыбираем процедуруУпроститьи получаем исходную функцию

◄
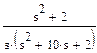