График в полярных координатах

Аналогично строятся графики в полярных координатах. Вводим пределы изменения угла q и формулы для функции r(q). Затем, выбираем в меню пункт Вставка->График->Полярные Координаты

Пример 2.Построить график функции .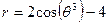

В автоматическом режиме:

Ранжирование переменной:

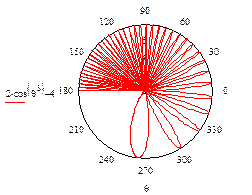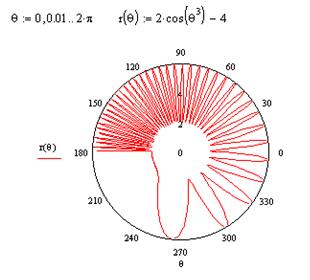
В одной системе координат можно строить несколько графиков функций, вводя эти функции через запятую.

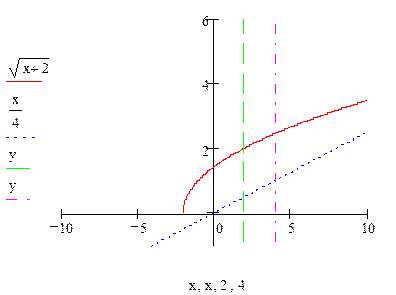
Пример 3. Изобразить область, ограниченную кривыми

а)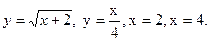

б) .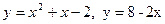

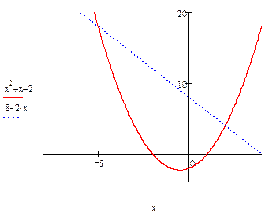График функции двух переменных

График функции двух переменных строится:

1) в автоматическом режиме.

Для этого вводим функцию двух переменных. Выбираем в меню Вставка->График->Поверхности. В нижней части появившегося прямоугольника вводим имя функции.

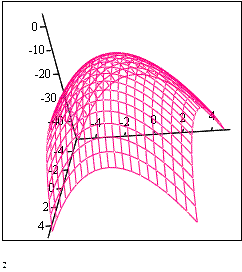
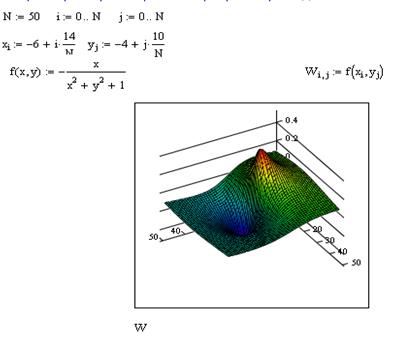
Пример 4. Построить поверхность 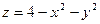в автоматическом режиме.

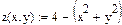2) ранжированием двух переменных.

Пример 5. Построить поверхности

а) 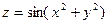; б) .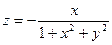

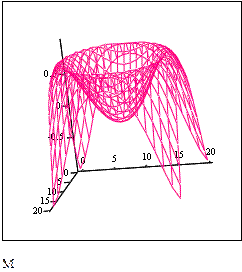
Пусть переменные i и j (индексы) принимают целые значения от 0 до N

N=20. Поверхность будет построена по 20 точкам.

Аргументы х и у будут дискретными, если их задать, например, так:

x_i=(-1.5+0.15i), у_j=(- 1.5+0.15j)

Водится функция: z(x,y):=sin(x²+y²)

Далее вводится индексированная матрица М_i,j, элементы которой есть значения функции: М_i,j=z(x_i,y_j).

Выбираем в меню Вставка->График->Поверхности. В нижней части появившегося прямоугольника вводим матрицу М

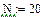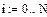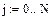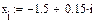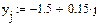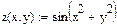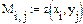Второй пример построения графика приведен ниже:

План выполнения работы

1. Решите примеры 1 −5.

2. Постойте график функции 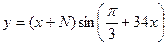и форматируйте его.

3. Постройте в автоматическом режиме и по 50 точкам поверхности:

а) ;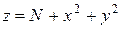

б)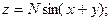

4. Постройте кривую в полярной системе координат .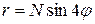

Контрольные вопросы

1. Каким способом вводится шаблон двумерных и трехмерных графиков?

2. Способы построения графиков.

3. Как можно просмотреть небольшой участок графика?

4. Как можно форматировать трехмерные графики?

5. Можно ли вращать трехмерные графики мышью?

Лабораторная работа №3

Решение алгебраических уравнений в Mathcad

Цель работы: изучить методы решения алгебраических уравнений, систем нелинейных уравнений.

Решение линейных алгебраических уравнений с одной переменной

Алгебраическое уравнение нужно представить в виде f(x)=0. В Mathcad

предусмотрено несколько способов решения таких уравнений.

I способ

Решение выполняется встроенной функцией: root(f(x),x)

Пример 1. Решить уравнение: cos(x) = x + 0.2

Чтобы решить его в Mathcad, нужно ввести начальное приближение к корню x=1, а далее:

root(cos(x) - x - 0.2,x) =

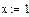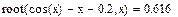Использование функции root требует предварительного задания начального приближения. Если исследуемая функция имеет много корней, то найденный корень будет зависить от начального приближения.

Если начальное приближение расположено близко к локальному экстремуму функции f, функция root может не найти корня, либо найденный корень будет далеко от начального приближения.

Начальное приближение к корню можно определить графически.

II способ

Решение выполняется встроенной функцией: solve

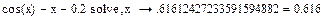III способ

Нахождение корней полинома с помощью функции polyroots(v), которая возвращает вектор, содержащий все корни многочлена, коэффициенты которого задаются вектором v. Если полином имеет рациональные или комплексно-сопряженные корни, то его можно разложить на множители с помощью процедуры factorменю символьных операций Symbolics

Пример 2. Найти корни полинома 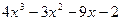и разложить его на множители.
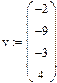
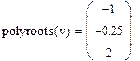
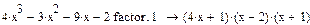