Движение точки в полярных координатах
Д.В. Кузьмин
КИНЕМАТИКА
Учебное пособие
Северодвинск
УДК 531 (075.8)
Кузьмин Д.В. Кинематика: учебное пособие. – Северодвинск: РИО Севмашвтуза, 2004. – 50 с.
Ответственный редактор ст. преподаватель каф. «Проектирование подъемно-транспортного и технологического оборудования» Севмашвтуза Л.А. Ковалев.
Рецензенты: Зав. каф. «Робототехнические системы, машины и оборудование лесного компекса» Архангельского государственного технического университета,
к.т.н., доцент Б.К. Микитюк;
Ведущий инженер НИТИЦ ФГУП ПО «Севмаш»
Ю.П. Голованов.
Учебное пособие «Кинематика» состоит из трех разделов: «Кинематика точки», «Кинематика твердого тела» и «Основы кинематики механической системы». Целью учебного пособия является оказание помощи студентам в установлении прочных взаимосвязей между лекционным курсом теоретической механики (раздел «Кинематика») и задачами, решаемыми на практических занятиях. В пособии дано строгое изложение основного теоретического материала с использованием современных математических методов и приведены подробно описанные примеры решения задач. Разделы «Кинематика точки» и «Кинематика твердого тела» предназначены для всех студентов, изучающих теоретическую механику; раздел «Основы кинематики механической системы» предназначен для студентов, учебная программа которых предусматривает углубленное изучение теоретической механики в течение двух семестров. Учебное пособие «Кинематика» может быть полезно студентам немеханических инженерных специальностей, изучающих дисциплину «Прикладная механика».
Печатается по решению редакционно-издательского совета Севмашвтуза
ISBN
© Севмашвтуз, 2004 г.
СОДЕРЖАНИЕ
1. КИНЕМАТИКА ТОЧКИ………………………………………………………...5
ООсновные понятия………………………………………………………................5
Векторный способ задания движения точки…………………………………..6
ККоординатный способ задания движения точки………………………………6
Естественный способ задания движения точки………………………..............8
ДДвижение точки в полярных координатах…………………………… ……..11
ВВопросы для проверки усвоения материала…………………………………..12
2. КИНЕМАТИКА ТВЕРДОГО ТЕЛА…………………………………………13
ООсновные понятия………………………………………………………………14
ЧЧисло степеней свободы твердого тела……………………………….............15
ВВекторно-матричный способ описания движения твердого тела…………...16
ВВращение твердого тела вокруг неподвижной точки……………………….17
ППроизвольное движение твердого тела……………………………..................18
ССкорость точки твердого тела в случае его произвольного
ддвижения…………………………………………………………………………19
УУскорение точки твердого тела в случае его произвольного
ддвижения…………………………………………………………………………21
ЧЧастные случаи движения твердого тела…………………………………….22
ВВращение вокруг неподвижной оси…………………………………………..23
ППлоское движение………………………………………………………………24
.Сложное движение точки………………………………………………………29
ВВопросы для проверки усвоения материала………………………………….38
3. ОСНОВЫ КИНЕМАТИКИ МЕХАНИЧЕСКОЙ СИСТЕМЫ………………...39
3.1. Классификация связей…………………………………………………….39
3.2. Ограничения, налагаемые связями на положения, скорости, ускорения и перемещения точек механической системы……………………………40
3.3. Действительные и виртуальные перемещения………………………….42
3.4. Обобщенные координаты…………………………………………………44
3.5. Вопросы для проверки усвоения материала……………………………..49
СПИСОК ЛИТЕРАТУРЫ………………………………………………………….50
КИНЕМАТИКА ТОЧКИ
Основные понятия
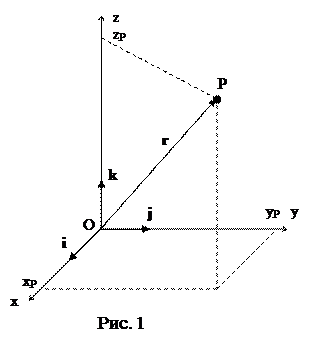
Кинематика точки изучает движение точки в трехмерном пространстве относительно начальной точки отсчета, которая полагается неподвижной. Например, начало отсчета может принадлежать неподвижному твердому телу. Тогда, совершая движение, точка будет изменять свое положение относительно начала отсчета с течением времени. Задать движение точки означает дать способ определения положения, скорости и ускорения точки в любой момент времени. Следовательно, задачей кинематики точки является разработка способов задания движения точки, а также методов определения ее скорости и ускорения. Положение точки P относительно начала отсчета удобно определять с помощью радиус-вектора положения (рис. 1):
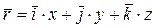 , (1)
, (1)
где 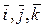 - единичные векторы, задающие в пространстве направления осей
- единичные векторы, задающие в пространстве направления осей 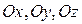 декартовой системы координат,
декартовой системы координат, 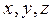 - координаты радиус-вектора положения точки. Так как координаты начала отсчета
- координаты радиус-вектора положения точки. Так как координаты начала отсчета 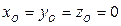 , то
, то 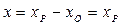 ,
, 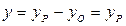 ,
, 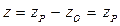 , т.е. координаты вектора положения совпадают с координатами точки P.
, т.е. координаты вектора положения совпадают с координатами точки P.
 | |||||
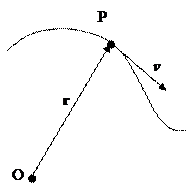 | |||||
| |||||
Выражение (1) называется геометрической формой задания 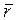 . Оно читается следующим образом: «чтобы получить
. Оно читается следующим образом: «чтобы получить 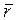 , отложим расстояние x в направлении
, отложим расстояние x в направлении 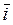 , прибавим к нему расстояние y в направлении
, прибавим к нему расстояние y в направлении 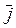 , затем прибавим еще расстояние z в направлении
, затем прибавим еще расстояние z в направлении 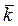 ». Кроме этого, существует координатная форма задания
». Кроме этого, существует координатная форма задания 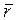 в виде вектора-столбца:
в виде вектора-столбца:
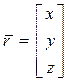 . (2)
. (2)
Формы задания вектора (1) и (2) используются в задачах математического описания движения точки.
Векторный способ задания движения точки
Радиус-вектор 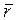 можно задать как вектор-функцию времени:
можно задать как вектор-функцию времени: 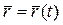 . С течением времени конец вектора
. С течением времени конец вектора 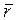 описывает траекторию точки P (рис.2). Производная от
описывает траекторию точки P (рис.2). Производная от 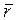 по времени t называется скоростью точки P:
по времени t называется скоростью точки P:
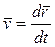 (3)
(3)
Производная от 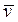 называется ускорением точки:
называется ускорением точки:
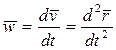 (4)
(4)
Вектор скорости всегда направлен по касательной к траектории в точке P, вектор ускорения – внутрь траектории, как будет показано в п. 1.4.
Координатный способ задания движения точки
Запишем вектор-функцию 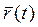 в форме (1):
в форме (1): 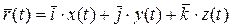 . Тогда скорость точки P будет иметь вид
. Тогда скорость точки P будет иметь вид 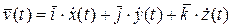 , где точкой обозначаются полные производные по времени t, т.е.
, где точкой обозначаются полные производные по времени t, т.е. 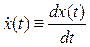 ,
, 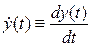 ,
, 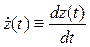 . Эти производные координат вектора
. Эти производные координат вектора 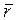 имеют геометрический смысл проекций вектора
имеют геометрический смысл проекций вектора 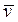 на оси Ox, Oy и Oz.
на оси Ox, Oy и Oz.
Величина скорости 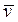 определяется равенством
определяется равенством
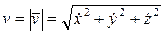 , (5)
, (5)
а направление вектора 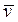 относительно осей Ox, Oy и Oz – направляющими косинусами[1]
относительно осей Ox, Oy и Oz – направляющими косинусами[1]
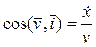 ,
, 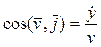 ,
, 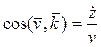 . (6)
. (6)
Ускорение точки P определяется равенством 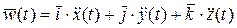 , где двумя точками обозначены вторые производные по времени t:
, где двумя точками обозначены вторые производные по времени t: 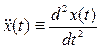 ,
, 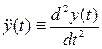 ,
, 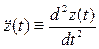 . Эти производные координат вектора
. Эти производные координат вектора 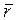 имеют геометрический смысл проекций вектора
имеют геометрический смысл проекций вектора 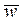 на оси Ox, Oy и Oz. Величина вектора ускорения и его направления определяются равенствами, аналогичными (5), (6). Таким образом, движение точки будет полностью заданным, если известны законы изменения ее координат:
на оси Ox, Oy и Oz. Величина вектора ускорения и его направления определяются равенствами, аналогичными (5), (6). Таким образом, движение точки будет полностью заданным, если известны законы изменения ее координат: 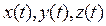 .
.
Задача
Задан закон движения точки P: 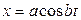 ,
, 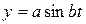 ,
, 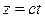 , где
, где 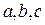 - постоянные. Найти траекторию, скорость и ускорение точки.
- постоянные. Найти траекторию, скорость и ускорение точки.
Решение
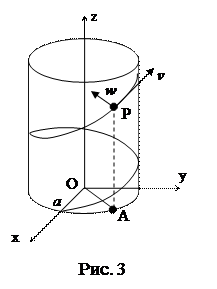
Возведя в квадрат первые равенства, и сложив их, получим 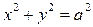 . Это показывает, что точка P движется по поверхности цилиндра радиуса a, ось которого совпадает с осью Oz (рис. 3). Пусть φ – угол между проекцией OA радиус-вектора OP на плоскость Oxy и осью Ox. Тогда
. Это показывает, что точка P движется по поверхности цилиндра радиуса a, ось которого совпадает с осью Oz (рис. 3). Пусть φ – угол между проекцией OA радиус-вектора OP на плоскость Oxy и осью Ox. Тогда 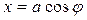 ,
, 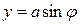 ,
, 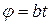 ,
, 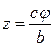 . Следовательно, отрезок OA равномерно вращается, а точка P равномерно перемещается по образующей AP. Таким образом, точка движется по винтовой линии.
. Следовательно, отрезок OA равномерно вращается, а точка P равномерно перемещается по образующей AP. Таким образом, точка движется по винтовой линии.
Определим скорость точки P: 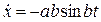 ,
, 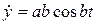 ,
, 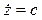 . Модуль скорости
. Модуль скорости 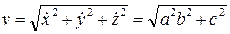 , т.е. величина вектора скорости постоянна, а ее направление изменяется со временем.
, т.е. величина вектора скорости постоянна, а ее направление изменяется со временем.
Ускорение точки P: 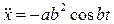 ,
, 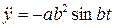 ,
, 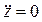 . Модуль ускорения
. Модуль ускорения 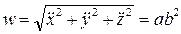 . Направляющие косинусы вектора ускорения
. Направляющие косинусы вектора ускорения 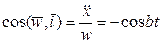 ,
, 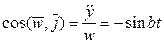 ,
, 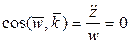 . Следовательно, ускорение точки P имеет постоянную величину и направлено по внутренней нормали цилиндра (рис. 3).
. Следовательно, ускорение точки P имеет постоянную величину и направлено по внутренней нормали цилиндра (рис. 3).
 | |||||
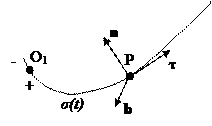 | |||||
| |||||
Естественный способ задания движения точки
Можно задать движение точки P, заранее определив ее траекторию σ относительно точки O. Тогда, на известной траектории выбирается начало отсчета дуговой координаты σ(t) точка O1 и положительное направление отсчета положения точки P (рис. 4). Такой способ задания движения точки называется естественным.
Для вычисления скорости и ускорения точки P при естественном способе задания движения введем правую тройку единичных векторов 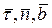 . Вектор
. Вектор 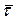 направлен по касательной к траектории в точке P, вектор
направлен по касательной к траектории в точке P, вектор 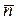 - по нормали. Вектор
- по нормали. Вектор 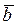 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 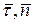 . Радиус-вектор точки P относительно точки O будет сложной функцией времени:
. Радиус-вектор точки P относительно точки O будет сложной функцией времени: 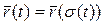 . Тогда скорость точки P будет определяться равенством
. Тогда скорость точки P будет определяться равенством
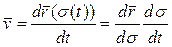 . (7)
. (7)
Вычислим производную 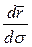 . Она равна
. Она равна 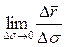 . Ясно, что при
. Ясно, что при 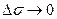 длина хорды
длина хорды 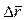 будет приближаться к длине соответствующей дуги
будет приближаться к длине соответствующей дуги 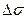 и
и 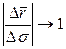 . При этом
. При этом 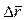 займет положение касательной к σ в точке P. Следовательно,
займет положение касательной к σ в точке P. Следовательно, 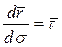 и равенство (7) запишется в виде
и равенство (7) запишется в виде
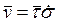 . (8)
. (8)
Равенство (8) показывает, что скорость точки P всегда направлена по касательной к траектории. Ускорение точки P, с учетом (8), имеет вид
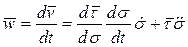 . (9)
. (9)
Вычислим производную 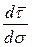 =
= 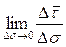 . Ясно, что единичный вектор
. Ясно, что единичный вектор 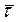 изменяется только по направлению при движении точки P по траектории σ. Приращение дуги представим в виде
изменяется только по направлению при движении точки P по траектории σ. Приращение дуги представим в виде 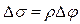 , где ρ – радиус кривизны траектории, Δφ – приращение угла поворота радиуса кривизны. Тогда можно записать
, где ρ – радиус кривизны траектории, Δφ – приращение угла поворота радиуса кривизны. Тогда можно записать 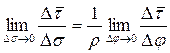 . При
. При 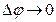 длина
длина 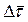 будет приближаться к величине угла
будет приближаться к величине угла 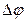 и
и 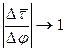 . При этом
. При этом 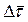 займет положение нормали к σ в точке P. Следовательно,
займет положение нормали к σ в точке P. Следовательно, 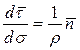 и равенство (9) запишется в виде
и равенство (9) запишется в виде
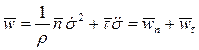 . (10)
. (10)
Соотношение (10) называется теоремой о разложении полного ускорения точки на нормальную 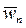 и тангенциальную
и тангенциальную 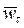 составляющие. Нормальное ускорение
составляющие. Нормальное ускорение 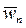 точки объясняется наличием кривизны траектории и характеризует изменение вектора скорости точки P по направлению. Тангенциальное ускорение
точки объясняется наличием кривизны траектории и характеризует изменение вектора скорости точки P по направлению. Тангенциальное ускорение 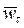 характеризует изменение вектора скорости точки P по величине. Если траектория точки – кривая, то в любом случае
характеризует изменение вектора скорости точки P по величине. Если траектория точки – кривая, то в любом случае 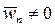 и вектор полного ускорения
и вектор полного ускорения 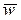 будет всегда направлен внутрь траектории.
будет всегда направлен внутрь траектории.
Задача
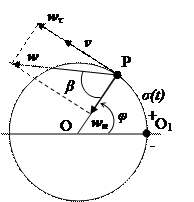
Точка P движется по окружности радиуса R, закон движения точки 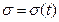 . Определить модуль полного ускорения точки и угол между полным ускорением и его нормальной составляющей.
. Определить модуль полного ускорения точки и угол между полным ускорением и его нормальной составляющей.
Решение
Так как 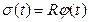 , из (8) и (10) следует, что
, из (8) и (10) следует, что 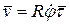 ,
, 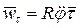 ,
, 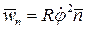 . Величины
. Величины  и
и 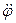 являются соответственно угловой скоростью и угловым ускорением радиуса OP = R (рис. 5). Обозначая
являются соответственно угловой скоростью и угловым ускорением радиуса OP = R (рис. 5). Обозначая 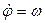 ,
, 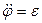 , получим выражение для модуля ускорения точки:
, получим выражение для модуля ускорения точки:
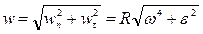 .
.
 Угол между полным ускорением и его нормальной составляющей определяется из равенства
Угол между полным ускорением и его нормальной составляющей определяется из равенства 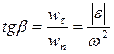 .
.
 | |||||
| |||||
| |||||
Задача
Движение точки P задано уравнениями: 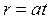 ,
, 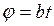 ,
, 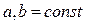 . Найти траекторию, скорость и ускорение точки.
. Найти траекторию, скорость и ускорение точки.
Решение
Исключив из данных уравнений время t, получим уравнение траектории 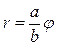 . Эта линия называется спиралью Архимеда. Согласно (11) имеем
. Эта линия называется спиралью Архимеда. Согласно (11) имеем
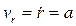 ,
, 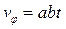 .
.
Величина скорости точки P: 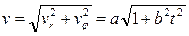 . Согласно (12) имеем
. Согласно (12) имеем
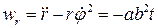 ,
, 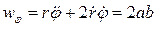 .
.
Величина ускорения точки P: 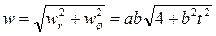 .
.
Вопросы для проверки усвоения материала
1) Сформулируйте задачу кинематики точки.
2) Что такое радиус-вектор положения точки?
3) Перечислите способы задания движения точки.
4) Дайте определения скорости и ускорения точки.
5) Как направлена скорость точки?
6) Сформулируйте теорему о разложении полного ускорения точки.
7) Почему ускорение точки всегда направлено внутрь траектории?
8) Какую систему координат называют полярной?
9) Как направлены радиальная и трансверсальная оси?
10) Как связаны между собой декартовая и полярная системы координат?
КИНЕМАТИКА ТВЕРДОГО ТЕЛА
Основные понятия
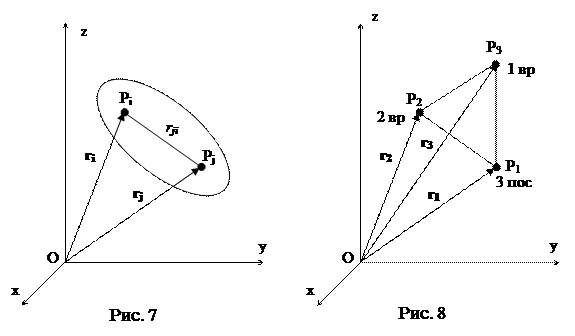
Абсолютно твердое тело – это такая механическая система, расстояние между любыми двумя точками которой всегда постоянно. Для краткости, абсолютно твердое тело называют просто твердым телом. Пусть твердое тело представляет собой механическую систему из некоторого числа точек 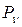 ,
, 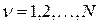 . Тогда для любой пары точек
. Тогда для любой пары точек 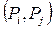 из этой системы справедливо утверждение
из этой системы справедливо утверждение 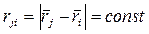 (рис. 7).
(рис. 7).
 |
Задача кинематики твердого тела состоит в разработке способов задания его движения, а также способов определения скоростей и ускорений точек твердого тела при помощи кинематических характеристик, общих для всего твердого тела.
Задача
В неподвижной системе координат OXYZ заданы радиус-векторы концов тонкого стержня AB: 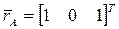 ,
, 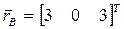 . Определить положение стержня после его поворота вокруг оси OZ на угол θ = 600.
. Определить положение стержня после его поворота вокруг оси OZ на угол θ = 600.
Решение
Введем систему координат Oxyz, жестко связанную со стержнем. Пусть начальное положение этой системы координат совпадает с положением осей неподвижной системы координат OXYZ. Тогда радиус-векторы точек A и B в этих системах координат будут совпадать: 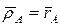 ,
, 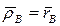 . Положение стержня после указанного поворота определится из соотношений:
. Положение стержня после указанного поворота определится из соотношений:
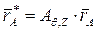 ,
, 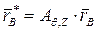 .
.
Выполняя вычисления, получим:
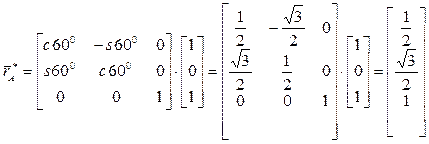 ;
;
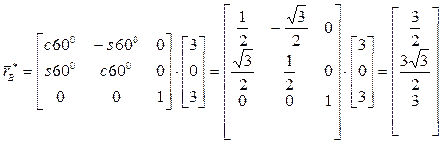 .
.
Начальное и конечное положения стержня приведены на рис. 10.
Задача
Определить конечное положение стержня AB из предыдущей задачи, если стержень после поворота на угол θ = 600 вокруг оси OZ совершил поступательное перемещение 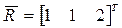 .
.
Решение
Введем абсолютную систему координат OaXYZ так, чтобы в начальном положении системы координат OaXYZ и OXYZ совпадали. Тогда конечные положения точек A и B стержня будут получены из соотношений:
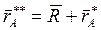 ,
, 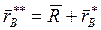 .
.
Выполняя вычисления, получим:
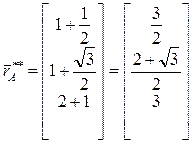 ,
, 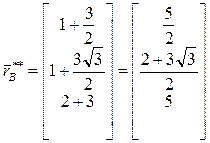 .
.
Начальное, промежуточное и конечное положения стержня, а также его перемещения изображены на рис. 12.
2.4. Скорость точки твердого тела в случае его произвольного движения
Пусть задан радиус-вектор некоторого центра O твердого тела 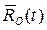 и матрица поворота A(t). Тогда скорость любой точки P, принадлежащей этому телу определится из соотношения:
и матрица поворота A(t). Тогда скорость любой точки P, принадлежащей этому телу определится из соотношения:
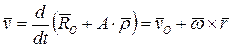 , (3)
, (3)
где 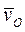 - абсолютная скорость центра O,
- абсолютная скорость центра O, 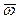 - угловая скорость твердого тела. Координаты вектора
- угловая скорость твердого тела. Координаты вектора 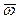 в системе координат OaXYZ определяются как элементы кососимметрической матрицы5
в системе координат OaXYZ определяются как элементы кососимметрической матрицы5
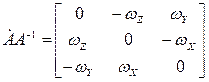 . (4)
. (4)
Скорость центра 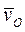 и угловая скорость
и угловая скорость 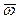 являются величинами, общими для всего твердого тела. Согласно (3), с их помощью можно вычислить скорость любой точки твердого тела относительно неподвижного начала отсчета.
являются величинами, общими для всего твердого тела. Согласно (3), с их помощью можно вычислить скорость любой точки твердого тела относительно неподвижного начала отсчета.
Задача
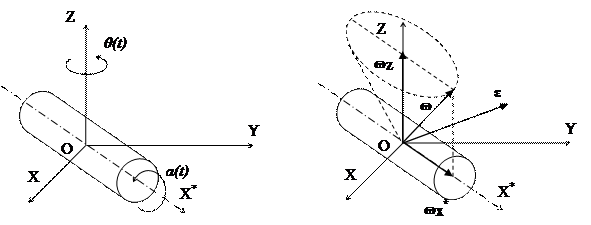
Вал, на котором укреплена зенитная пушка, вращается вокруг своей оси OX* по закону 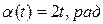 и одновременно поворачивается вокруг оси OZ неподвижной системы координат OXYZ по закону
и одновременно поворачивается вокруг оси OZ неподвижной системы координат OXYZ по закону 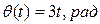 (рис. 13). Определить угловую скорость вала.
(рис. 13). Определить угловую скорость вала.
 | |||||
| |||||
| |||||
Решение
По условию задачи, вал вращается вокруг неподвижной точки O. Найдем матрицу поворота вала:
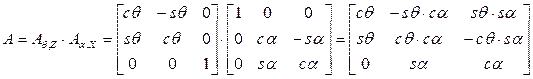 .
.
Вектор угловой скорости вала 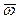 найдем согласно (4). Для этого выполним следующие вычисления:
найдем согласно (4). Для этого выполним следующие вычисления:
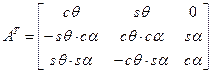 ;
; 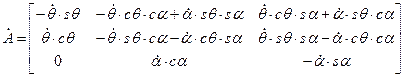 .
.
Учитывая, что 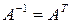 , получаем:
, получаем:
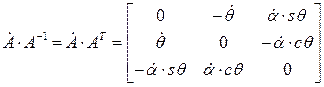 , откуда
, откуда 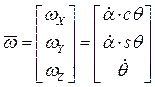 .
.
Модуль вектора угловой скорости: 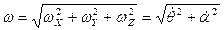 . Подставляя исходные данные
. Подставляя исходные данные 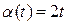 ,
, 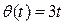 в полученные соотношения, окончательно будем иметь:
в полученные соотношения, окончательно будем иметь:
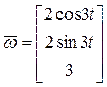 ,
, 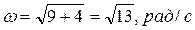 .
.
Таким образом, вектор угловой скорости вала имеет постоянную величину 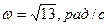 и вращается вокруг оси OZ по закону
и вращается вокруг оси OZ по закону 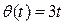 (рис. 14).
(рис. 14).
2.5. Ускорение точки твердого тела в случае его произвольного движения
Ускорение точки P, принадлежащей твердому телу, вычисляется в соответствии с соотношением:
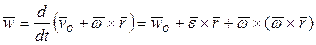 , (5)
, (5)
где 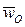 - ускорение центра O,
- ускорение центра O, 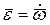 - угловое ускорение твердого тела. Слагаемое
- угловое ускорение твердого тела. Слагаемое 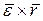 называют вращательным, а
называют вращательным, а 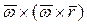 - осестремительным ускорением. Ускорение центра
- осестремительным ускорением. Ускорение центра 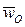 и угловое ускорение
и угловое ускорение 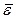 являются величинами, общими для всего твердого тела.
являются величинами, общими для всего твердого тела.
Задача
Вычислить угловое ускорение вала из задачи п. 2.4.
Решение
Угловое ускорение найдем, продифференцировав по времени t вектор угловой скорости:
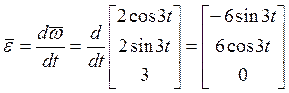 .
.
Модуль углового ускорения: 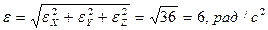 . Таким образом, угловое ускорение вала постоянно по величине, находится в плоскости OXY нормально к
. Таким образом, угловое ускорение вала постоянно по величине, находится в плоскости OXY нормально к 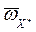 и вращается вокруг оси OZ вместе с вектором
и вращается вокруг оси OZ вместе с вектором 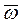 (рис. 14).
(рис. 14).
Плоское движение
Движение твердого тела называется плоским, если все точки тела движутся в плоскостях, параллельных неподвижной плоскости.
 | |||||
 | |||||
| |||||
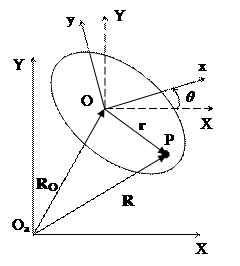
Плоское движение твердого тела эквивалентно движению соответствующей плоской фигуры в собственной плоскости (рис. 16). Фигура имеет свободу по трем независимым перемещениям: вдоль оси OaX, вдоль оси OaY и вращение в плоскости OaXY. Соответственно, любое положение фигуры может быть задано тремя координатами: XO, YO, θ.
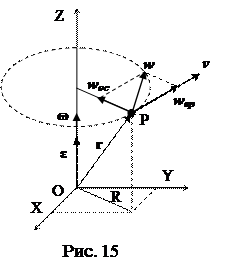
Формулы для скорости и ускорения точки P твердого тела, совершающего плоское движение, получаются из общих соотношений (3) и (5) путем применения к этим соотношениям частных условий:
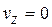 ,
, 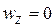 ,
, 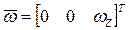 .
.
В результате из (3) следует7
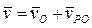 , (8)
, (8)
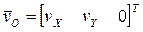 ,
, 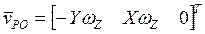 ,
, 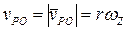 ,
,
а из (5)
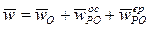 , (9)
, (9)
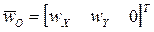 ,
, 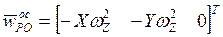 ,
, 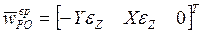 ,
,
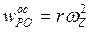 ,
, 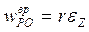 .
.
Таким образом, в случае плоского движения, векторы скорости и ускорения точки твердого тела всегда лежат в плоскости движения, а векторы угловой скорости и углового ускорения всегда перпендикулярны этой плоскости. Этот факт позволяет при решении практических задач оперировать линейными скоростями и ускорениями как векторами в плоскости, а угловыми скоростями и ускорениями – как скалярными величинами.
Задача
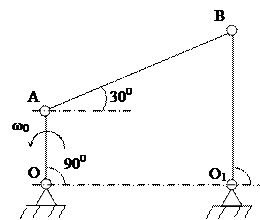
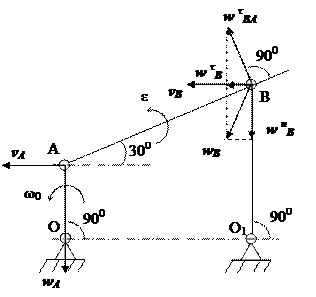 Стержень OA шарнирного четырехзвенника (рис. 17) вращается с постоянной угловой скоростью ω0. Определить угловую скорость, угловое ускорение стержня AB, а также ускорение шарнира B в положении, указанном на рисунке, если AB = 2OA = 2a.
Стержень OA шарнирного четырехзвенника (рис. 17) вращается с постоянной угловой скоростью ω0. Определить угловую скорость, угловое ускорение стержня AB, а также ускорение шарнира B в положении, указанном на рисунке, если AB = 2OA = 2a.
 | |||||
| |||||
| |||||
Решение
Стержень AB изображенного на рисунке четырехзвенного механизма совершает плоское движение, а стержни OA и O1B вращаются вокруг неподвижных центров O и O1. Найдем скорость шарнира A:
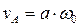 .
.
Вектор 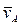 перпендикулярен OA и направлен в сторону вращения стержня OA (рис. 18). Для скорости шарнира B справедливо равенство (8):
перпендикулярен OA и направлен в сторону вращения стержня OA (рис. 18). Для скорости шарнира B справедливо равенство (8):
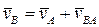 ,
,
причем направление 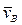 , согласно положению механизма, будет то же, что и у
, согласно положению механизма, будет то же, что и у 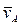 . Из этого следует, что
. Из этого следует, что 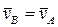 ,
, 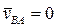 ,
, 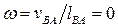 , т.е. стержень AB совершает мгновенно-поступательное движение.
, т.е. стержень AB совершает мгновенно-поступательное движение.
Найдем ускорение шарнира A. Так как этот шарнир движется вокруг неподвижной точки O, то для его ускорения справедливо равенство (7):
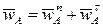 ,
,
где 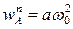 - нормальное ускорение, направленное от точки A к центру вращения O;
- нормальное ускорение, направленное от точки A к центру вращения O; 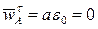 , т.к.
, т.к. 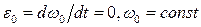 . В данном случае
. В данном случае 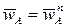 . Для ускорения шарнира B справедливо равенство (9):
. Для ускорения шарнира B справедливо равенство (9):
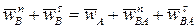 , (10)
, (10)
где 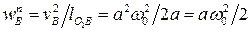 - нормальное ускорение шарнира B в его движении вокруг неподвижной точки O1;
- нормальное ускорение шарнира B в его движении вокруг неподвижной точки O1; 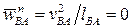 - нормальное ускорение шарнира B относительно точки A.
- нормальное ускорение шарнира B относительно точки A.
Неизвестные по величине векторы 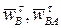 определим, построив план ускорений. Для этого из произвольной точки pw, называемой полюсом плана ускорений, отложим отрезок pwa,, отображающий ускорение
определим, построив план ускорений. Для этого из произвольной точки pw, называемой полюсом плана ускорений, отложим отрезок pwa,, отображающий ускорение 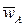 (рис. 19). Тогда, проводя через точку a прямую, перпендикулярную AB, получим направление тангенциального ускорения
(рис. 19). Тогда, проводя через точку a прямую, перпендикулярную AB, получим направление тангенциального ускорения 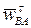 . Составляющую результирующего ускорения
. Составляющую результирующего ускорения 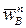 отложим из полюса pw в виде отрезка pwb*, длина которого вдвое меньше pwa. Замкнем план ускорений прямой, перпендикулярной стержню O1B и задающей направление
отложим из полюса pw в виде отрезка pwb*, длина которого вдвое меньше pwa. Замкнем план ускорений прямой, перпендикулярной стержню O1B и задающей направление 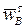 . На пересечении двух перпендикуляров получим точку b. Отрезок pwb будет отображать ускорение
. На пересечении двух перпендикуляров получим точку b. Отрезок pwb будет отображать ускорение 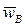 шарнира B, а отрезок ab – ускорение
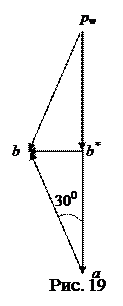
шарнира B, а отрезок ab – ускорение 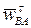 . План ускорений графически отображает векторное равенство (10), из плана легко определяются все неизвестные ускорения:
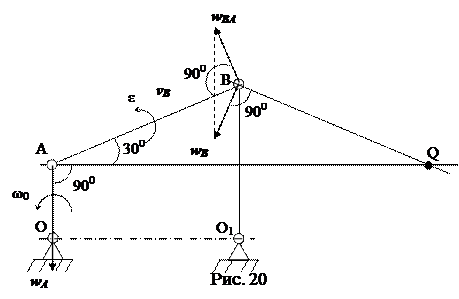
. План ускорений графически отображает векторное равенство (10), из плана легко определяются все неизвестные ускорения:
 | |||
 | |||
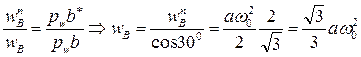 - ускорение шарнира B;
- ускорение шарнира B;
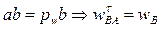 ,
, 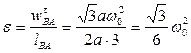 - угловое ускорение стержня AB. Направления всех вычисленных скоростей и ускорений точек механизма изображены на рис. 18.
- угловое ускорение стержня AB. Направления всех вычисленных скоростей и ускорений точек механизма изображены на рис. 18.
В задачах на случай плоского движения твердого тела иногда удается получить более короткое решение за счет использования понятий мгновенный центр скоростей и мгновенный центр ускорений. Мгновенным центром скоростей (МЦС) называют такую точку плоской фигуры, скорость которой в данный момент времени движения равна нулю. Скорости остальных точек фигуры при этом такие, какие они были бы при вращательном движении фигуры вокруг МЦС. Мгновенный центр ускорений (МЦУ), соответственно, это такая точка плоской фигуры, ускорение которой в данный момент времени движения равно нулю. Ускорения остальных точек фигуры такие, какие они были бы при ее вращательном движении относительно МЦУ.
Решим предыдущую задачу, используя понятия МЦС и МЦУ. Из рис. 17 видно, что стержень OA параллелен стержню O1B. Следовательно, абсолютные скорости точек A и B стержня AB параллельны. Учитывая, что в силу неизменности расстояния между точками A и B проекции скоростей 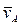 и
и 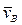 на направление AB должны быть одинаковыми (точка B не может догнать точку A, но также не может отстать от точки A), заключаем, что
на направление AB должны быть одинаковыми (точка B не может догнать точку A, но также не может отстать от точки A), заключаем, что 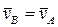 . Таким образом, стержень AB совершает мгновенно-поступательное движение, положение его МЦС бесконечно удалено и
. Таким образом, стержень AB совершает мгновенно-поступательное движение, положение его МЦС бесконечно удалено и 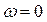 .
.
Определим направление ускорения 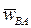 точки B в ее движении относительно точки A. Так как угловая скорость стержня AB
точки B в ее движении относительно точки A. Так как угловая скорость стержня AB 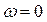 , то
, то 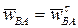 и, следовательно, угол между
и, следовательно, угол между 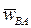 и AB равен 900 (рис. 20). Согласно определению понятия МЦУ угол между абсолютным ускорением
и AB равен 900 (рис. 20). Согласно определению понятия МЦУ угол между абсолютным ускорением 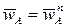 и направлением на МЦУ (точка Q) также равен 900. Для определения положения точки Q воспользуемся соотношением, справедливым при
и направлением на МЦУ (точка Q) также равен 900. Для определения положения точки Q воспользуемся соотношением, справедливым при 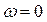 :
:
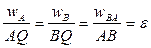 . (11)
. (11)
Вычислим ускорение точки A: 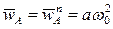 . В силу соотношения
. В силу соотношения 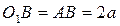 будем иметь
будем иметь 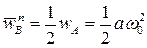 . Так как
. Так как 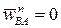 , а
, а 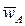 направлено в ту же сторону, что и
направлено в ту же сторону, что и 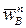 , на основании равенства (10) заключаем:
, на основании равенства (10) заключаем: 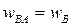 (рис. 19). Следовательно, из (11) получим
(рис. 19). Следовательно, из (11) получим 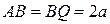 , и точка Q будет симметрична точке A относительно направления O1B (рис. 20). Тогда
, и точка Q будет симметрична точке A относительно направления O1B (рис. 20). Тогда 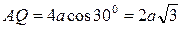 ,
, 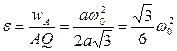 и
и 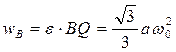 . Угол между
. Угол между 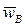 и направлением BQ, согласно определению понятия МЦУ, составит 900.
и направлением BQ, согласно определению понятия МЦУ, составит 900.
Сложное движение точки
Движение точки называется сложным, если оно происходит относительно двух систем координат, одна из которых – подвижная, а другая – неподвижная. Движение точки относительно подвижной системы координат называется относительным, а движение подвижной системы координат относительно неподвижной – переносным. Часто подвижную систему координат связывают с некоторым твердым телом, совершающим движение относительно неподвижной системы координат. При этом полагается, что относительное и переносное движения известны. Задача состоит в том, чтобы определить сложное движение точки в неподвижной (абсолютной) системе координат.
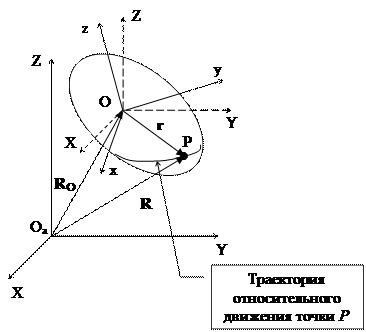 Пусть точка P перемещается по поверхности твердого тела, движущегося произвольным образом относительно абсолютной системы координат OaXYZ (рис. 21).
Пусть точка P перемещается по поверхности твердого тела, движущегося произвольным образом относительно абсолютной системы координат OaXYZ (рис. 21).
|
Система координат OXYZ движется поступате
