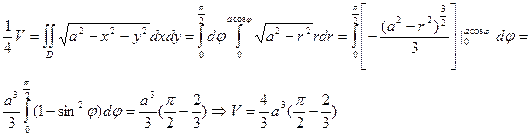Двойной интеграл в полярных координатах

Применим формулу (**) к преобразованию с помощью полярных координат (обозначения общепринятые)

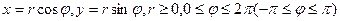
Якобиан будет равен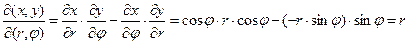

Тогда 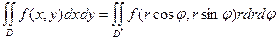(***), где

D и 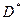- соответствующие друг другу области в плоскостях OXY и 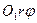(здесь r и 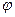рассматриваются как декартовы координаты точки).

Например, пусть D - полукруг радиуса R, расположенный в полуплоскости 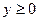. Во вспомогательной плоскости 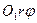ему соответствует прямоугольник 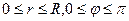(здесь точке (0,0) плоскости OXY соответствует отрезок на оси в плоскости . Это нарушение взаимной однозначности происходит на границе области , при этом формулы преобразования сохраняются).

Если D - весь круг радиуса R, то ему соответствует прямоугольник

R

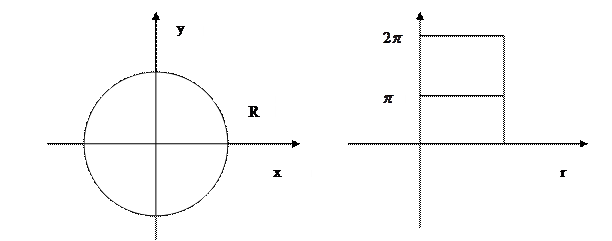
Формулу для элемента площади в полярных координатах можно получить из геометрических соображений. Построим в плоскости OXY координатные линии для полярной системы координат: r=const, 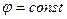. Они разбивают плоскость на криволинейные четырехугольники, ограниченные дугами концентрических окружностей и их радиусами.

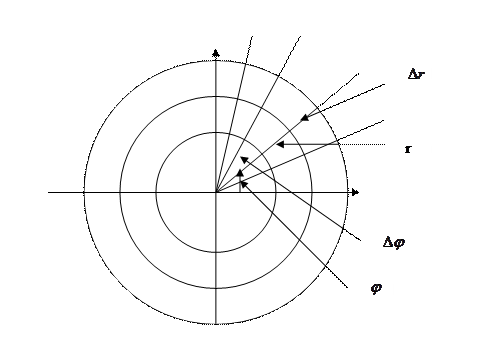
Рассмотрим выделенный четырехугольник.

Его площадь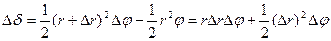

Второе слагаемое – бесконечно малая величина более высокого порядка, чем первое слагаемое. Отбрасывая его получим приближенное равенство 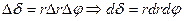, а это приводит к формуле (***).

Замечание Чтобы привести двойной интеграл в полярных координатах к повторному, обычно нет необходимости строить область 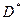, во вспомогательной плоскости 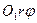, а можно просто руководствоваться следующими правилами:

1. Пусть полюс содержится внутри области интегрирования D, заключенной между лучами 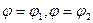и линии 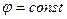встречают ее границу не более чем в двух точках.

Возможны такие области

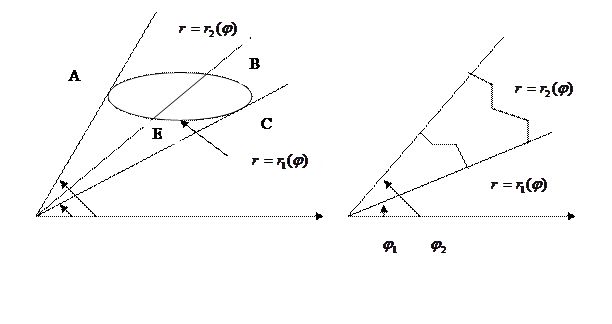
Полярными уравнениями кривых AEC и ABC пусть будут . Обе функции непрерывны в замкнутом интервале 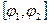. Интегрируя сначала по r в пределах его изменения при постоянном , то есть от 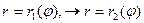, а затем по 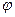от 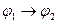получим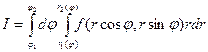

Интегрирование в обратном порядке, то есть сначала по 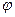, а затем по r обычно не встречается.

Если линия ACE (левый рисунок) стягивается в точку 0, то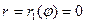

В частном случае, когда областью интегрирования служит часть кругового кольца 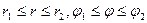пределы интегрирования постоянны по обеим переменным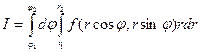

2. Пусть полюс содержится внутри области интегрирования. Полярный радиус пересекает границу в одной точке. Интегрируя сначала по r, затем по 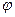, получаем 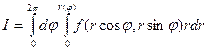, где 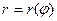- полярное уравнение границы области.

В частности, когда 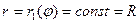, то есть, когда область интегрирования есть круг с центром в полюсе, получаем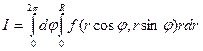

Примеры

1. Расставить пределы интегрирования в полярных координатах, если D – круг .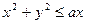

Решение. Переходя к полярным координатам, получим уравнение окружности в виде 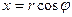. Тогда 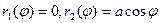. Пределы изменения по 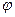от 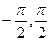. Получаем следующий интеграл .

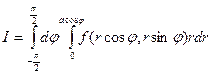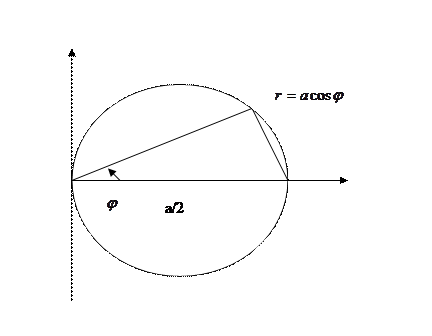
2. Вычислить объем общей части шара радиуса а и кругового цилиндра радиуса а/2 при условии, что центр шара лежит на боковой поверхности цилиндра.

Решение

Система координат расположена следующим образом: ось OZ лежит на боковой поверхности цилиндра, ось ОХ совпадает с диаметром цилиндра и радиусом шара. В силу симметрии измеряемого тела относительно плоскостей OXY и OXZ, можно вычислить четвертую часть объема, заключенного в первом октанте. Получаем

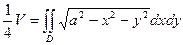, где D – полукруг, являющийся половиной основания цилиндра. Удобно преобразовать двойной интеграл к полярным координатам. Полярное уравнение полуокружности, ограничивающей область D - 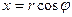(см. предыдущий пример). Сначала интегрируем по r, затем по .