Множество комплексных чисел.

Обозначается K.

ib

z=a+ib

arg z

a

Положим, что число – это радиус-вектор.

Тогда R – множество радиус-векторов числовой оси.

K – множество радиус-векторов плоскости, содержащей числовую ось.

z – радиус-вектор. z∈K.

|z| - длина радиус-вектора.

α = arg z – аргумент (угол между направлением оси действительных чисел и направлением радиус-вектора.

a+ib – форма представления комплексного числа, где a – действительная часть комплексного числа, b – коэффициент при мнимой части, i – мнимая единица, i²=-1.

|z| = √a² +b²

arg z = arctg

cos α =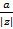

sin α =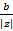

z = |z|(cos α + i sin α) – тригонометрическая форма комплексного числа

zⁿ = (|z|( cos α + i sin α)ⁿ = |z|ⁿ (cos nα + i sin nα)

12. Действия над комплексными числами.

· Сравнение.

a + bi = c +di ⇔ a=c и b=d

· Сложение.

(a + bi) + (c + di) = (a + c) + (b + d)i

· Вычитание.

(a + bi) – (c + di) = (a – c) + (b – d)i

· Умножение.

§ Из книжки:

z – произведение z₁ и z₂

|z| = |z₁| * |z₂|

arg z = arg z₁ + arg z₂

§ Еще откуда-то: (просто раскрыть скобки и, когда появится i², заменить её на -1)

(a + bi)(c + di) = (ac – bd) + (bc + ad)i

· Деление.
1) Составляем дробь.
2) Умножаем числитель и знаменатель на сопряжённое знаменателю выражение.
3) Раскрываем скобки в числителе, в знаменателе – формула.
a+bi/c-di = (a+bi)(c+di)/(c-di)(c+di)

Формула Муавра.

Нужна для возведения компл. числа в степень и извлечения корня n-ной степени. (Нужно сначала представить компл. число в тригонометрической форме).

zⁿ=|z|ⁿ(cos(nα) + i sin(nα)

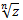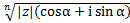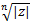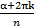= = (cos + i sin )
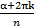Для любого компл. числа есть n корней n-ной степени.
k – меняется от 0 до n-1 в зависимости от номера корня (т.е. если n=2 то, всего 2 корня, а k может быть 0 и 1)

14. Последовательности и их пределы.

Числовую функцию f(n)=a, заданную на множестве натуральных чисел, называют числовой последовательностью. Говорят, что последовательность задана, если каждому натуральному числу n по некоторому закону f поставлено в соответствие число f(n).
Если закон f задан формулой – аналитическое задание последовательности. При нём записывают аналитическое выражение для общего члена a_n.
Способ построения очередного члена последовательности по предыдущим называется рекуррентным.

Существуют убывающие и возрастающие последовательности.

Ограниченная сверху последовательность – существует число M такое, что a_n<M для всех n.

Ограниченная снизу последовательность – существует число M такое, что a_n>M для всех n.

Ограниченная последовательность – последовательность, ограниченная и сверху, и снизу.

Последовательность {x_n} – бесконечно большая, если для любого A>0 (сколь бы большим его ни взяли) существует номер N такой, что для всех членов последовательности с номерами n>N выполняется |x_n|>A.

Последовательность {a_n} – бесконечно малая: для всех n>N выполняется |a_n|< 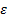( 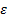– очень малое).

Последовательность {a_n} сходится к числу A, если для любого сколь угодно малого 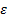>0 можно указать такое n₀( 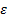)∈N, что для всех n>n₀ выполняется |a_n – A|< .

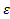Если последовательность имеет пределом точку A, то для всех номеров последовательности, начиная с некоторого n₀, члены последовательности находятся внутри отрезка 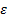(A- ; A+ 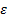), называемого 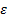-окрестностью числа A.

Почти все числа {a_n} попадают в 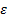-окрестность.

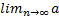_n = A – предел.

Если последовательность не имеет конечного предела или не имеет предела вообще, то ее называют расходящейся.