Дифференциальное уравнение теплопроводности — уравнение Фурье для Декартовых координат.
Дифференциальное уравнение теплопроводности
Связь между величинами, участвующими в передаче теплоты теплопроводностью, устанавливается так называемым дифференциальным уравнением теплопроводности, на основе которого строится математическая теория теплопроводности. В основу вывода дифференциального уравнения теплопроводности положен закон сохранения энергии, сочетаемый с законом Фурье.
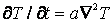 . (2.24)
. (2.24)
Уравнение (2.24) называется дифференциальным уравнением теплопроводности (или дифференциальным уравнением Фурье) для трехмерного нестационарного температурного поля при отсутствии внутренних источников теплоты. Оно является основным при изучении вопросов нагревания и охлаждения тел в процессе передачи теплоты теплопроводностью и устанавливает связь междувременным и пространственным изменениям температуры в любой точке поля. Температуропроводность 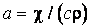 является физическим параметром вещества и имеет единицу м2/c. В нестационарных тепловых процессах a характеризует скорость изменения температуры.
является физическим параметром вещества и имеет единицу м2/c. В нестационарных тепловых процессах a характеризует скорость изменения температуры.
Из уравнения (2.24) следует, что изменение температуры во времени 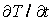 для любой точки тела пропорционально величине a. Поэтому при одинаковых условиях быстрее увеличивается температура у того тела, которое имеет большуютемпературопроводность.
для любой точки тела пропорционально величине a. Поэтому при одинаковых условиях быстрее увеличивается температура у того тела, которое имеет большуютемпературопроводность.
Дифференциальное уравнение теплопроводности с источником теплоты внутри тела имеет вид:
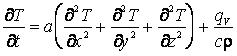 , (2.25) где qV — удельная мощность источника, то есть количество выделяемой теплоты в единице объёма вещества в единицу времени.
, (2.25) где qV — удельная мощность источника, то есть количество выделяемой теплоты в единице объёма вещества в единицу времени.
Это уравнение записано в декартовых координатах. В других координатах оператор Лапласа имеет иной вид, поэтому меняется и вид уравнения. Например, в цилиндрических координатах дифференциальное уравнение теплопроводности с внутренним источником теплоты таково:
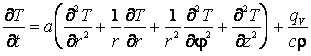 , (2.26)
, (2.26)
где r — радиус-вектор в цилиндрической системе координат;
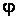 — полярный угол.
— полярный угол.
39. Условия однозначности для процессов теплопроводности.
Так как дифференциальное уравнение теплопроводности получены на основе общих законов физики, то оно описывает явление теплопроводности в самом общем виде. Поэтому можно сказать, что полученное дифференциальное уравнение описывает целый класс явлений теплопроводности.Чтобы из бесчисленного количества выделить конкретный процесс и дать его полный математическое описание, к дифференциального уравнения необходимо добавить математическое описание всех отдельных особенностей процесса, который рассматривается. Эти отдельные особенности, вместе с дифференциальным уравнением дают полный математическое описание конкретного процесса теплопроводности, называется условиями однозначности или краевыми условиями.
Условия однозначности включают:
- Геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс;
- Физические условия, характеризующие физические свойства тела;
- Временные или начальные условия, характеризующие распределение температур в теле, исследуемой в начальный момент времени;
- Граничные условия, характеризующие взаимодействие тела, рассматриваемого с окружающей средой.
Геометрическими условиями задаются форма и линейные размеры тела, в котором протекает процесс.
Физическими условиями задаются физические параметры тела X, с, р и др.. и может быть задан закон распределения внутренних источников теплоты.
