Глава 8. Дифференциальные уравнения

Глава 8. Дифференциальные уравнения

§ 1. Общие сведения о дифференциальных уравнениях

П. 1. Основные понятия

Определение 1.При решении различных задач математики, физики, химии и других наук часто пользуются математическими моделями в виде уравнений связывающих независимую переменную, искомую функцию и ее производные. Такие уравнения называются дифференциальными уравнениями. Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.

Так, решением уравнения является функция – первообразная для функции .

Рассмотрим некоторые общие сведения о дифференциальных уравнениях (ДУ).

Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называют обыкновенным; в противном случае – ДУ в частных производных. Далее будем рассматривать только обыкновенные ДУ.

Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения.

Например, уравнение – обыкновенное ДУ третьего порядка, а уравнение – первого порядка.

Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ – интегральной кривой.

Рассмотрим некоторые задачи, решение которых приводит к дифференциальным уравнениям.

Дифференциальные уравнения первого порядка

П. 1. Основные понятия

ДУ первого порядка в общем случае можно записать в виде 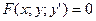(1).

Уравнение связывает независимую переменную x, искомую функцию y и ее производную y’. Если уравнение (1) можно разрешить относительно y’, то его записывают в виде y’ = f(x; y) (2) и называют ДУ первого порядка, разрешенным относительно производной.

Уравнение (2) устанавливает связь (зависимость) между координатами точки (x; y) и угловым коэффициентом y’ касательной к интегральной кривой, проходящей через эту точку. Следовательно, ДУ y’ = f(x; y) дает совокупность направлений (поле направлений) на плоскости Oxy. Таково геометрическоеистолкование ДУ первого порядка.

Кривая, во всех точках которой направление поля одинаково, называется изоклиной. Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить y’ = c, т.е. f(x; y) = c.

ДУ первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме: 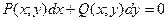(3), где P(x; y) и Q(x; y) – известные функции. Уравнение (3) удобно тем, что переменные x и y в нем равноправны, т.е. любую из них можно рассматривать как функцию другой. Отметим, что от одного вида записи ДУ можно перейти к другому.

Интегрирование ДУ в общем виде приводит к бесконечному множеству решений (отличающихся друг от друга постоянными величинами).

Чтобы решение ДУ приобрело конкретный смысл, его надо подчинить некоторым дополнительным условиям.

Условие, что при x = x₀ функция y должна быть равна заданному числу y₀, т.е. y = y₀ называется начальным условием. Начальное условие записывается в виде y(x₀) = y₀ (4).

Определение 1. Общим решением ДУ первого порядка называется функция y = φ(x; c), содержащая одну произвольную постоянную и удовлетворяющая условиям:

1. Функция φ(x; c) является решением ДУ при каждом фиксированном значении с.

2. Каково вы ни было начальное условие (4), можно найти такое значение постоянной с = с₀, что функция y = φ(x; c₀) удовлетворяет начальному условию.

Определение 2. Частным решением ДУ первого порядка называется любая функция y = φ(x; c₀), полученная из общего решения y = φ(x; c) при конкретном значении постоянной с = с₀.

Если общее решение ДУ найдено в неявном виде, т.е. в идее уравнения Φ (x; y; c) = 0, то такое решение называется общим интегралом ДУ. Уравнение Φ (x; y; c₀) = 0 в этом случае называется частным интегралом уравнения.

С геометрической точки зрения y = φ(x; c) есть семейство интегральных кривых на плоскости Oxy; частное решение y = φ(x; c₀) – одна кривая из этого семейства, проходящая через точку (x₀; y₀).

Определение 3.Задача отыскания решения ДУ первого порядка (3), удовлетворяющего заданному начальному условию (4), называется задачей Коши.

Теорема (существования и единственности решения задачи Коши). Если в уравнении (2) функция f(x; y) и ее частная производная f’_y(x; y) непрерывны в некоторой области D, содержащей точку (x₀; y₀), то существует единственное решение y = φ этого уравнения, удовлетворяющее начальному условию (4).

Геометрический смысл теоремы состоит в том, что при выполнении ее условий существует единственная интегральная кривая ДУ, проходящая через точку (x₀; y₀).

Метод Бернулли.

Решение уравнения (1) ищется в виде произведения двух других функций, т.е. с помощью подстановки y = uv, где u = u(x), v = v(x) – неизвестные функции от x, причем одна из них произвольная (но не равна нулю– действительно любую функцию y(x) можно записать как ). Тогда . Подставляя выражения y и y’ в уравнение (1), получаем: или (2). Подберем функцию v = v(x) так, чтобы выражение в скобках было равно нулю, т.е. решим ДУ . Итак, , т.е. . Интегрируя, получаем . Ввиду свободы выбора функции v(x), можно принять c = 1. Отсюда . Подставляя найденную функцию v в уравнение (2), получаем . Получено уравнение с разделяющимися переменными. Решаем его: , , . Возвращаясь к переменной y, получаем решение исходного ДУ(1).

Уравнение Я. Бернулли

Определение 7.Уравнение вида (1) называется уравнением Бернулли.

Покажем, что его можно привести к линейному.

Если n = 0, то ДУ (1) – линейное, а при n = 1 – с разделяющимися переменными.

В общем случае, разделив уравнение (1) на yⁿ ≠0, получим: (2). Обозначим . Тогда . Отсюда находим . Уравнение (2) принимает вид .

Последнее уравнение является линейным относительно z. Решение его известно. Таким образом, подстановка сводит уравнение (1) к линейному. На практике ДУ (1) удобнее искать методом Бернулли в виде (не сводя его к линейному).

Уравнение Лагранжа

Определение 9. Уравнение вида 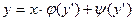(1), где φ и ψ – известные функции от 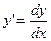, называется уравнением Лагранжа.

Введем вспомогательный параметр, положив y’ = p. Тогда уравнение (1) примет вид 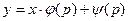(2). Дифференцируя по x, получим: 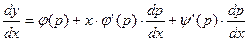, т.е. 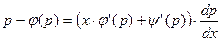или 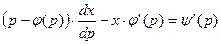(3). Уравнение (3) есть линейное уравнение относительно неизвестной функции x = x(p). Решив его, найдем: x = λ(p; c) (4). Исключая параметр p из уравнений (2) и (4), получаем общий интеграл уравнения (1) в виде y = γ(x; c).

Отметим, что, переходя к уравнению (3), мы делили на 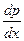. При этом могли быть утеряны решения, для которых 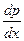=0, т.е. p = p₀ = const. Это значение p₀ является корнем уравнения p – φ(p) = 0.

Решение 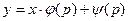является особям решением для уравнения (1).

Уравнение Клеро

Рассмотрим частный случай уравнения Лагранжа при φ(y’) ≡ y’. Уравнение (1) принимает вид 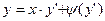(5) и называется уравнением Клеро.

Положив y’ = p, получаем: 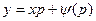(6).

Дифференцируя по x, имеем: 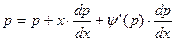, или 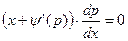. Если 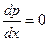, то p = c. Поэтому, с учетом формулы (6) имеем общее решение 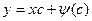(7).

Если 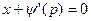, то получаем частное решение уравнения в параметрической форме: 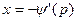, 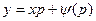. Это решение – особое решение уравнения Клеро: оно не содержится в формуле общего решения уравнения.

П.1. Основные понятия

ДУ порядка выше первого называются ДУ высших порядков. ДУ второго порядка в общем случае записывается в виде (1), или, если это возможно, в виде, разрешенном относительно старшей производной: (2).

Определение 1. Решением ДУ (2) называется функция , которая при подстановке в уравнение обращает его в тождество.

Определение 2. Общим решением ДУ (2) называется функция , где c₁ и c₂ – не зависящие от x произвольные постоянные, удовлетворяющая условиям:

1) φ(x; c₁; c₂) является решением ДУ для каждого фиксированного значения c₁ и c₂.

2) Каковы бы ни были начальные условия y(x₀) = y₀, y’(x₀) = y’₀ (3) существуют единственные значения постоянных и такие, что функция является решением уравнения (2) и удовлетворяет начальным условиям (3).

Определение 3.Всякое решение уравнения (2), получающееся из общего решения при конкретных значениях постоянных и , называется частным решением.

Решения ДУ (2), записанные в виде называются общим и частным интегралом соответственно.

График всякого решения ДУ второго порядка называется интегральной кривой. Общее решение ДУ (2) представляет собой множество интегральных кривых; частное решение – одна интегральная кривая этого множества, проходящая через точку (x₀; y₀) и имеющая в ней касательную с заданным угловым коэффициентом .

Переписав ДУ (1) в виде , видим, что ДУ второго порядка устанавливает связь между координатами точки (x; y) интегральной кривой, угловым коэффициентом k = y’ касательной к ней и кривизной в точке (x; y). В этом состоит геометрическое истолкование ДУ второго порядка.

Как и в случае уравнения первого порядка, задача нахождения решения ДУ (2), удовлетворяющего заданным начальным условиям (3), называется задачей Коши.

Теорема 1 (существования и единственности задачи Коши). Если в уравнении (2) функция и ее частные производные f’_y и f’_y’ непрерывны в некоторой области D изменения переменных x, y, y’, то для всякой точки (x₀; y₀; y’₀) D существует единственное решение уравнения (2), удовлетворяющее начальным условиям (3).

Аналогичные понятия и определения имеют место для ДУ n-го порядка, которое в общем виде записывается как или (4), если его можно разрешить относительно старшей производной.

Начальные условия для ДУ (4) имеют вид (5).

Общее решение ДУ n-го порядка является функцией вида , содержащей n произвольных, независящих от x, постоянных.

Решение ДУ (4), получающееся из общего решения при конкретных значениях постоянных , называется частным решением.

Задача Коши для ДУ n-го порядка: найти решение ДУ (4), удовлетворяющее начальным условиям (5).

Проинтегрировать (решить) ДУ n-го порядка означает следующее: найти его общее или частное решение (интеграл) в зависимости от того, заданы начальные условия или нет.

Задача нахождения ДУ n-го порядка сложнее, чем первого. Поэтому рассмотрим лишь отдельные виды ДУ высших порядков.

Основные понятия

Многие задачи математики, механики, электротехники и других технических наук приводят к линейным дифференциальным уравнениям.

Определение 4. Уравнение вида (1), где – заданные функции, называется линейным ДУ n-го порядка.

Оно содержит искомую функцию y и все ее производные лишь в первой степени. Функции называются коэффициентами уравнения (1), а функция g(x) – его свободным членом.

Определение 5.Если свободный член g(x) ≡ 0, то уравнение (1) называется линейным однородным уравнением, если g(x) ≠ 0, то уравнение (1) называется неоднородным.

Разделив уравнение (1) на b₀(x) ≠ 0 и обозначив , запишем уравнение (1) в виде приведенного: (2).

Далее будем рассматривать линейные ДУ вида (2) и считать, что коэффициенты и свободный член уравнения (2) являются непрерывными функциями (на некотором интервале (a; b)). При этих условиях справедлива теорема существования и единственности решения ДУ.

П. 1. Основные понятия

Для решения многих задач математики, физики, техники (задач динамики криволинейного движения; задач электротехники для нескольких электрических цепей; определения состава системы, в которой протекают несколько последовательных химических реакций I порядка; отыскания векторных линий поля и других) нередко требуется несколько функций. Нахождение этих функций может привести к нескольким ДУ, образующим систему.

Определение 1. Системой ДУ называется совокупность ДУ, каждое из которых содержит независимую переменную, искомые функции и их производные.

Общий вид системы ДУ первого порядка, содержащей n искомых функций y₁, y₂, …, y_n, следующий: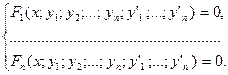

Определение 2.Система ДУ первого порядка, разрешенных относительно производной, т.е. система вида

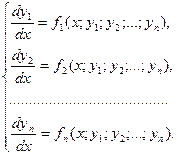(1) называется нормальной системой ДУ. При этом предполагается, что число уравнений равно числу искомых функций.

Замечание. Во многих случаях системы уравнений и уравнения высших порядков можно привести к нормальной системе вида (1).

Определение 3. Решением системы(1) называется совокупность из n функций y₁, y₂, …, y_n, удовлетворяющих каждому из уравнений этой системы.

Начальные условия для системы (1) имеют вид 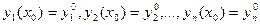(2).

Задача Коши для системы (1) ставится следующим образом: найти решение системы (1), удовлетворяющее начальным условиям (2).

Условия существования и единственности решения задачи Коши описывает теорема, приводимая здесь без доказательства.

Теорема Коши. Если в системе (1) все функции 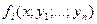непрерывны вместе со всеми своими производными по y_i в некоторой области D ((n + 1)-мерного пространства), то в каждой точке 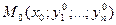этой области существует, и притом единственное, решение y₁ = φ₁(x), …, y_n = φ_n(x) системы, удовлетворяющее начальным условиям (2).

Меняя в области D точку M₀ (т.е. начальные условия), получим бесчисленное множество решений, которое можно записать в виде решения, зависящего от n произвольных постоянных: ,..., .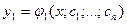

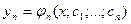Это решение является общим, если по заданным начальным условиям (2) можно однозначно определить постоянные c₁, c₂, …, c_n из системы уравнений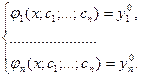

Решение, получающееся из общего при конкретных значениях постоянных c₁, c₂, …, c_n, называется частным решением системы (1).

Глава 8. Дифференциальные уравнения

§ 1. Общие сведения о дифференциальных уравнениях

П. 1. Основные понятия

Определение 1.При решении различных задач математики, физики, химии и других наук часто пользуются математическими моделями в виде уравнений связывающих независимую переменную, искомую функцию и ее производные. Такие уравнения называются дифференциальными уравнениями. Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.

Так, решением уравнения является функция – первообразная для функции .

Рассмотрим некоторые общие сведения о дифференциальных уравнениях (ДУ).

Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называют обыкновенным; в противном случае – ДУ в частных производных. Далее будем рассматривать только обыкновенные ДУ.

Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения.

Например, уравнение – обыкновенное ДУ третьего порядка, а уравнение – первого порядка.

Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ – интегральной кривой.

Рассмотрим некоторые задачи, решение которых приводит к дифференциальным уравнениям.