Системы уравнений четырехполюсника
Рассмотрим пассивный четырехполюсник, обозначив пары его зажимов 1-1’ и 2-2’ (рис.9.2).
Напряжение на зажимах 1-1’ обозначим U1, а на зажимах 2-2’ – U2. Токи, относящиеся к зажимам 1-1’ обозначим I1, а к зажимам 2-2’ – I2.
 |
Пусть направления токов соответствуют I1 и I2; такое направление токов называют прямой передачей. Если направления токов противоположны I1’ и I2’, то это обратная передача.
Соотношения между токами и напряжениями на входе и выходе четырехполюсника в зависимости от направлений токов описываются шестью формами уравнений.
Форма 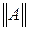 используется при прямой передаче (прямом включении четырехполюсника) и выражает зависимость напряжения и тока на входе четырехполюсника от напряжения и тока на выходе (рис. 9.3).
используется при прямой передаче (прямом включении четырехполюсника) и выражает зависимость напряжения и тока на входе четырехполюсника от напряжения и тока на выходе (рис. 9.3).
 |
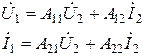 .
. Форма 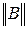 позволяет выразить напряжение и ток на выходе четырехполюсника через напряжение и ток на входе и используется при обратной передаче (рис. 9.4)
позволяет выразить напряжение и ток на выходе четырехполюсника через напряжение и ток на входе и используется при обратной передаче (рис. 9.4)
 |
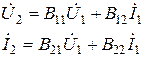 .
. Часто при использовании этих двух форм вместо коэффициентов А11, А12, А21, А22  и В11, В12, В21, В22 используют коэффициенты A, B, C, D. В этом случае уравнения в
и В11, В12, В21, В22 используют коэффициенты A, B, C, D. В этом случае уравнения в 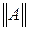 и
и 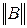 формах примут следующий вид:
формах примут следующий вид:
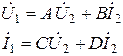 и
и 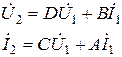 .
.
Параметры A,B,C,D называются коэффициентами или постоянными четырехполюсника. Они зависят от конфигурации схемы четырехполюсника, величин входящих в него сопротивлений и от частоты. Коэффициент В имеет размерность сопротивления, коэффициент С – проводимости, коэффициенты A и D безразмерны.
Если четырехполюсник обратимый, то для него определитель системы уравнений равен 1, то есть
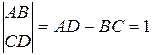 .
.
Для симметричного четырехполюсника A = D.
Мы рассмотрели два варианта направления токов. В радиотехнике и электронике часто используется третий вариант передачи, при котором входной и выходной токи направлены в сторону четырехполюсника (рис. 9.5).
 |
Для такого направления токов используют четыре различных формы уравнений.
 форма позволяет выразить токи на входе и выходе четырехполюсника через напряжения на входе и выходе:
форма позволяет выразить токи на входе и выходе четырехполюсника через напряжения на входе и выходе:
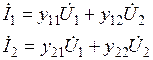 .
.
Все коэффициенты у имеют размерность проводимостей.
 форма позволяет выразить напряжения на входе и выходе четырехполюсника через входной и выходной токи:
форма позволяет выразить напряжения на входе и выходе четырехполюсника через входной и выходной токи:
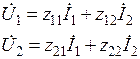 .
.
Все коэффициенты имеют размерность сопротивлений.
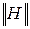 форма устанавливает зависимость напряжения на входе и тока на выходе от входного тока и выходного напряжения:
форма устанавливает зависимость напряжения на входе и тока на выходе от входного тока и выходного напряжения:
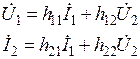 .
.
Здесь h11 имеет размерность сопротивления; h22 – размерность проводимости; h12 и h21 – безразмерные величины.
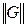 форма устанавливает связь между током на входе и напряжением на выходе с напряжением на входе и током на выходе:
форма устанавливает связь между током на входе и напряжением на выходе с напряжением на входе и током на выходе:
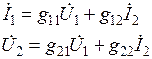 .
.
Коэффициент g11 имеет размерность проводимости; g22 – сопротивления; коэффициенты g12 и g21 безразмерны.
Коэффициенты всех форм уравнений взаимосвязаны, и путем несложных преобразований можно перейти от коэффициентов одной формы к коэффициенам другой. Формулы перехода от одних коэффициентов к другим приводятся в справочной литературе.
