Экспериментальной определение взаимной индуктивности
И однополярных зажимов катушек
Для того чтобы экспериментально определить взаимную индуктивность, необходимо провести два опыта.
1. Соединяем катушки согласно. Подаем на вход цепи напряжение U и измеряем ток при согласном включении Iсогл.
По известным значениям напряжения и тока определяем zсогл:
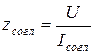 .
.
2. Соединяем катушки встречно. Подаем на вход цепи то же самое напряжение U и определяем ток при встречном включении Iвстр.
Находим сопротивление при встречном включении:
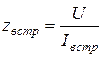 .
.
Воспользуемся выражениями для сопротивлений при согласном и встречном включениях
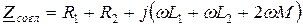 ;
;
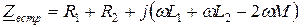 .
.
Найдем разность сопротивлений при согласном и встречном включении:
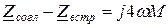 .
.
Отсюда 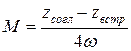 .
.
Если у индуктивно связанных катушек не обозначены начала и концы обмоток, то их можно определить опытным путем.
Для этого у одной катушки условно полагаем один зажим началом, другой – концом. Зажимы второй катушки обозначим, допустим, а и b.
Соединяем эти катушки последовательно, подключая вторую катушку произвольно, как, например, на рис. 8.10.
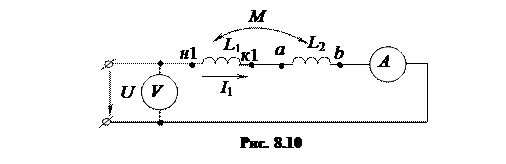
Подаем на вход цепи напряжение U и измеряем ток I1.
Меняем местами зажимы второй катушки (рис. 8.11) и при том же напряжении U измеряем ток I2.
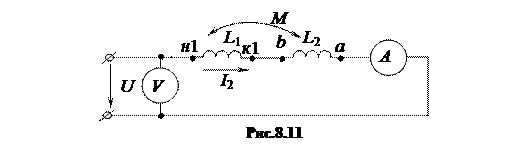
Сравниваем измеренные токи. Так как при согласном включении сопротивление больше, чем при встречном, то при одинаковом напряжении ток согласного включения будет меньше, чем встречного.
Если I1 > I2, то в первом случае было встречное включение, значит, зажим а является концом катушки, b – началом.
Если I1 < I2, то в первом случае было согласное включение и зажим а является началом катушки, b – концом.
Параллельное соединение индуктивно связанных катушек
Рассмотрим особенности цепей с индуктивно связанными катушками, соединенными параллельно. Для простоты расчетов будем полагать, что катушки идеальные, то есть не обладают активным сопротивлением.
Согласное включение
Схема замещения параллельно соединенных катушек при согласном включении показана на рис. 8.12.
Для независимых контуров схемы можно записать следующие уравнения:
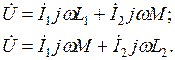
Из этих выражений определим токи İ1 и İ2:
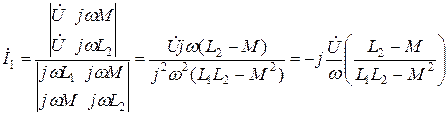
Аналогично можно определить второй ток:
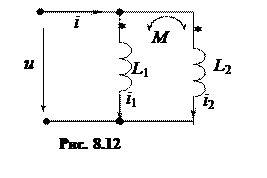
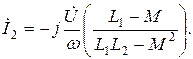
Всегда произведение индуктивностей больше, чем квадрат взаимной индуктивности L1L2 > M2, cледовательно, разность L1L2 – M2 > 0. Подберем коэффициент k таким образом, чтобы выполнялось равенство k2L1L2 = M2, тогда величина этого коэффициента определится выражением
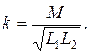
Коэффициент k называется коэффициентом связи катушек. Всегда k < 1.
Определим общий ток в цепи, считая, что L1 > M, L2 > M:
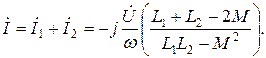
Из этого выражения находим
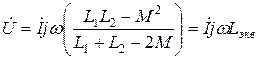 ,
,
где Lэкв – эквивалентная индуктивность цепи:
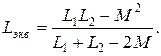
Рассмотрим частный случай.
Подберем катушки таким образом, чтобы L2 < M < L1. В этом случае выражения для токов примут вид:
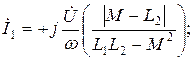
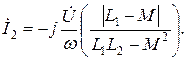
Ток İ1 будет опережать напряжение 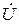 на π/2, то есть в ветви с током İ1 наблюдается емкостный эффект. При этом ток İ1 имеет направление, обратное току İ2 и выражение для общего тока İ примет следующий вид:
на π/2, то есть в ветви с током İ1 наблюдается емкостный эффект. При этом ток İ1 имеет направление, обратное току İ2 и выражение для общего тока İ примет следующий вид:
İ = -İ1 + İ2 или İ2 = İ + İ1.
С энергетической точки зрения данный процесс объясняется следующим образом.
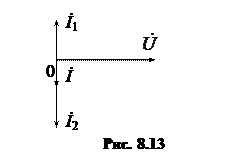 В катушку L2энергия поступает двумя путями: электрическим путем непосредственно из сети; магнитным путем через взаимную индуктивность М от катушки L1, которая является, как и сеть, генератором по отношению к катушке L2.
В катушку L2энергия поступает двумя путями: электрическим путем непосредственно из сети; магнитным путем через взаимную индуктивность М от катушки L1, которая является, как и сеть, генератором по отношению к катушке L2. 
Емкостный эффект наблюдается только внутри схемы, ее некоторой части. Общий же ток İ никогда не будет емкостным, так как в целом цепь имеет индуктивный характер и всегда эквивалентная индуктивность положительна Lэкв > 0.
Векторная диаграмма токов представлена на рис. 8.13.
Встречное включение
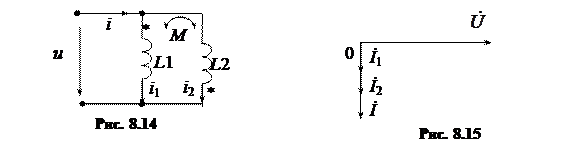 |
Схема параллельного соединения катушек при встречном включении показана на рис. 8.14.
По аналогии с предыдущим при встречном параллельном включении катушек выражения для токов будут иметь следующий вид:
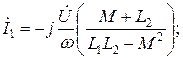
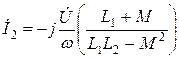 ;
;
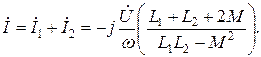
То есть в выражениях для токов изменяется только знак взаимной индуктивности.
Все токи всегда отстают от напряжения. Емкостный эффект при встречном параллельном включении катушек отсутствует.
Векторная диаграмма для этого случая показана на рис. 8.15.
Воздушный трансформатор
Свойства магнитосвязанных контуров используются в специальных устройствах, предназначенных для преобразования величин тока и напряжения. Такие устройства называются трансформаторами.
Простейший трансформатор состоит из двух электрически несоединенных и неподвижных друг относительно друга катушек, называемых обмотками трансформатора. Эти катушки связаны между собой путем взаимной индукции.
Если обмотки трансформатора намотаны на ферромагнитный сердечник, то такой трансформатор будет обладать нелинейными свойствами. Трансформатор без сердечника является линейным. Магнитная связь в таком трансформаторе осуществляется только через воздух, поэтому трансформатор называется воздушным.
Вследствие линейности воздушного трансформатора его можно рассчитывать, используя законы и правила линейных электрических цепей, и описывать происходящие в нем процессы линейными уравнениями
Схема замещения воздушного трансформатора представлена на рис. 8.16.
 |
Обмотка R1,L1, к которой приложено преобразуемое напряжение, называется первичной. Обмотка с параметрами R2,L2 называется вторичной и к ней присоединён приёмник Zн. Включение обмоток согласно правилу Ленца встречное.
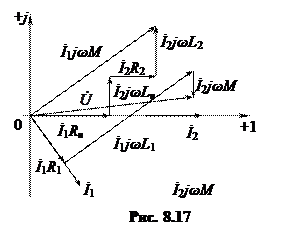 Запишем уравнения по второму закону Кирхгофа для входного и выходного контуров трансформатора:
Запишем уравнения по второму закону Кирхгофа для входного и выходного контуров трансформатора:
İ1R1+ j ωL1İ1–jωMİ2 = 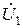 ,
,
İ2R2 + jωL2İ2 –jωMİ1 + 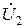 = 0.
= 0.
Построим векторную диаграмму, считая нагрузку активно-индуктивной Zн = Rн + jXн. Построение начинаем с тока İ2, совмещая последний с действительной осью +1. Диаграмму строим в соответствии с уравнениями трансформатора, последовательно изображая на комплексной плоскости векторы
İ2→İ2Rн→İ2jωLн→İ2R2→İ2jωL2→İ1jωM→İ1→İ1R1→İ1jωL1→İ2jωM→ 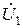 .
.
Векторная диаграмма представлена на рис. 8.17.
