Тема: Кривые второго порядка

Вершина параболы 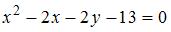имеет координаты …

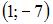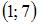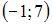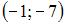Решение:
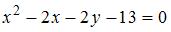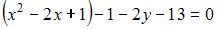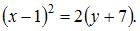Выделим в уравнении полный квадрат: или Тогда вершина параболы имеет координаты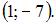

61. Тема: Кривые второго порядка
Центр окружности 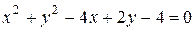имеет координаты …

Решение:
Выделим в уравнении 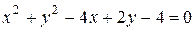полные квадраты: 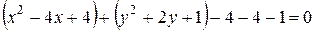или 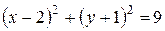. Тогда центр окружности имеет координаты .

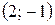Тема: Кривые второго порядка

Точк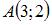и и 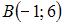являются концами одного из диаметров окружности. Тогда уравнение окружности имеет вид …

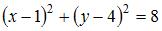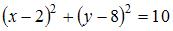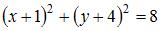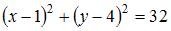Решение:
Окружность радиуса R с центром в точке 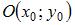задается на плоскости уравнением 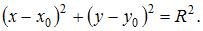Центр окружности имеет координаты середины отрезка AB: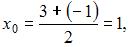 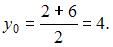Радиус окружности равен 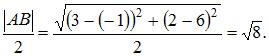Тогда уравнение окружности примет вид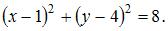

Тема: Кривые второго порядка

Эксцентриситет гиперболы 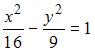равен …

			1,25
			0,8
			0,6
			6,25

Решение:
Эксцентриситет гиперболы 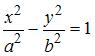вычисляется по формул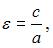е где 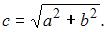Тогда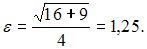

Тема: Кривые второго порядка

Фокусы эллипса 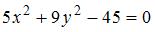имеют координаты …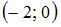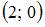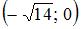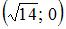

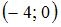			и
			и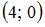
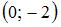			и
			и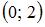

Решение:
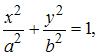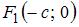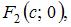Фокусы эллипса, заданного каноническим уравнением имеют координаты и где 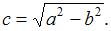Приведем уравнение эллипса 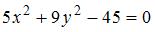к каноническому виду: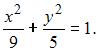
Тогда 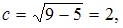то есть фокусы эллипса имеют координаты 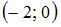и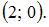

Тема: Кривые второго порядка

Фокусы эллипса лежат на оси абсцисс симметрично относительно начала координат, а длины полуосей равны соответственно 7 и 2. Тогда каноническое уравнение эллипса имеет вид …

Решение:
Каноническое уравнение эллипса: 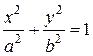. Так как 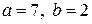, то каноническое уравнение эллипса имеет вид 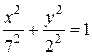или .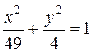

Тема: Кривые второго порядка

Парабола, вершина которой находится в начале координат, симметрична относительно оси Ox и проходит через точку 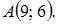Тогда уравнение параболы имеет вид …

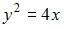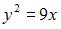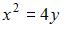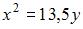Решение:
Каноническое уравнение параболы, проходящей через начало координат и симметричной относительно оси Ox имеет вид: 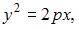где p – параметр параболы. Координаты точки 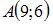удовлетворяют уравнению параболы, то есть 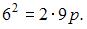Отсюда 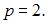Тогда уравнение параболы примет вид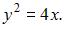

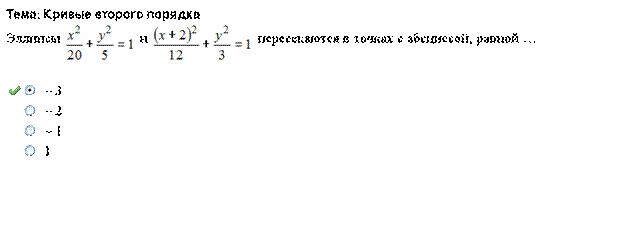
Асимптоты гиперболы 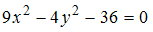задаются уравнениями …

Выберите один из 4 вариантов ответа:

1)

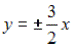
2)

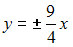
3)

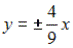
4)

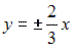
Верный ответ (1 б.): 1;

Решение:
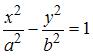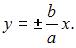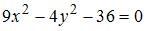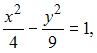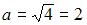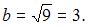Асимптоты гиперболы задаются уравнениями вида Разделив обе части уравнения на 36, получим каноническое уравнение гиперболы то есть и Тогда уравнения асимптот примут вид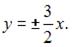

Тема: Прямая на плоскости

1. Уравнение прямой, проходящей через точку 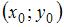с угловым коэффициентом 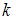, имеет вид: .

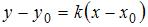2. Прямая, проходящая через две данные точк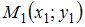и и 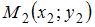, задается уравнением вида: .

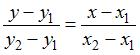Тема: Прямая на плоскости
Прямая линия проходит через точк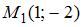и и 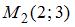. Тогда она пересекает ось 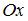в точке …

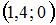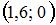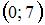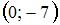Решение:
Прямая, проходящая через две данные точк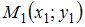и и 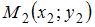, задается уравнением вида: 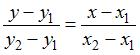. Тогда 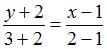, или 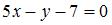. Точка, лежащая на оси 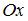, имеет координаты 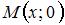. Тогда 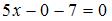и 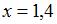.