Определение абсолютного ускорения точки.
| Теорема сложения ускорений (метод полюса) | Графическое нахождение 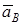 из векторного уравнения из векторного уравнения | Аналитическое нахождение 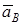 из векторного уравнения из векторного уравнения |
Абсолютное ускорение 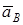 любой точки B тела равно векторной сумме ускорения любой точки B тела равно векторной сумме ускорения 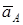 полюса A и ускорения полюса A и ускорения 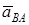 точки B в относительном движении точки вокруг полюса A: точки B в относительном движении точки вокруг полюса A: 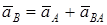 , или , или 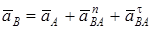 . (1) Вектор . (1) Вектор 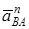 (нормальное ускорение точки B в движении вокруг полюса A) направлен от точки B к полюсу A. Модуль (нормальное ускорение точки B в движении вокруг полюса A) направлен от точки B к полюсу A. Модуль 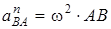 . Вектор . Вектор  (касательное ускорение точки B в движении вокруг полюса A) (касательное ускорение точки B в движении вокруг полюса A) 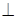 AB. Модуль AB. Модуль 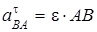 . . 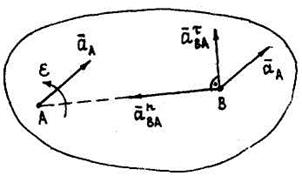 | Находим (если это возможно) векторы, содержащиеся в правой части (1). Выбираем масштаб и в соответствии с уравнением (1) строим векторный многоугольник. Вектор, проведенный из начала первого в конец последнего вектора, дает абсолютное ускорение 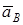 точки. точки.  | Выбираем оси координат и проектируем уравнение (1) на эти оси: 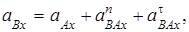 (2) (2) 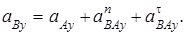 (3) Решая (2), (3) и учитывая, что точка B, кроме звена AB, принадлежит еще ползуну или кривошипу, находим (3) Решая (2), (3) и учитывая, что точка B, кроме звена AB, принадлежит еще ползуну или кривошипу, находим 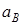 и и 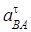 . Тогда . Тогда 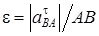 . . |
Пример К4. Механизм (рис. К4a) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами О1 и О2 шарнирами.
Дано: 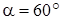 ,
, 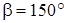 ,
, 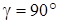 ,
, 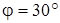 ,
, 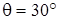 ,AD=DB,
,AD=DB, 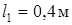 ,
, 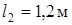 ,
, 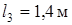 ,
, 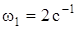 ,
, 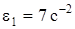 (направления
(направления 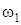 и
и 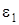 – против хода часовой стрелки).
– против хода часовой стрелки).
Определить:VB, VE, w2, aB, e3.
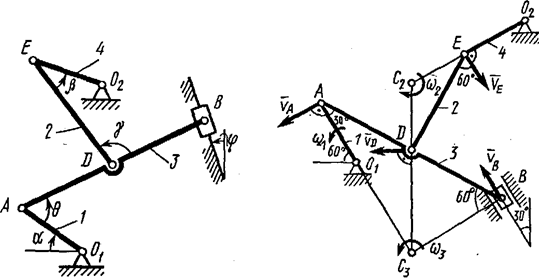
Рис. K4a Рис. K4б
Решение. 1. Строим положение механизма в соответствии с заданными углами и длинами стержней (рис. К4б; на этом рисунке в процессе решения задачи изображаем все векторы скоростей).
2. Определяем VB. Точка B принадлежит стержню 3, совершающему плоскопараллельное движение. Чтобы найти 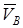 , нужно знать направление
, нужно знать направление  и скорость другой точки звена 3. Такой точкой является точка A, принадлежащая еще звену 1 (звено вращается, см. задачу К2).
и скорость другой точки звена 3. Такой точкой является точка A, принадлежащая еще звену 1 (звено вращается, см. задачу К2).
VA = w1l1 = 0,8 м/c;  . (1)
. (1)
Направление 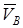 найдем, учитывая, что точка B принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная
найдем, учитывая, что точка B принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная 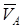 и направление
и направление 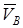 , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня 3) на прямую, соединяющую эти точки (прямая AB). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня 3) на прямую, соединяющую эти точки (прямая AB). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 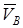 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
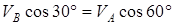 и VB = 0,46 м/c. (2)
и VB = 0,46 м/c. (2)
3. Определяем 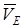 . Точка Е принадлежит стержню 2, совершающему плоскопараллельное движение. Следовательно, по аналогии с предыдущим, чтобы определить
. Точка Е принадлежит стержню 2, совершающему плоскопараллельное движение. Следовательно, по аналогии с предыдущим, чтобы определить 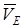 , надо сначала найти скорость точки D, принадлежащей одновременно стержню 3. Для этого, зная
, надо сначала найти скорость точки D, принадлежащей одновременно стержню 3. Для этого, зная 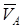 и
и 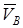 , строим мгновенный центр скоростей (МЦС) стержня АВ; это точка C3, лежащая на пересечении перпендикуляров к
, строим мгновенный центр скоростей (МЦС) стержня АВ; это точка C3, лежащая на пересечении перпендикуляров к 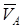 и
и 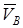 , восставленных из точек A и B. По направлению вектора
, восставленных из точек A и B. По направлению вектора 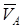 определяем направление мгновенного поворота стержня 3 вокруг МЦС C3. Вектор
определяем направление мгновенного поворота стержня 3 вокруг МЦС C3. Вектор 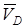 перпендикулярен отрезку C3D, соединяющему точки D и C3, и направлен в сторону мгновенного поворота тела. Величину VD найдем из пропорции
перпендикулярен отрезку C3D, соединяющему точки D и C3, и направлен в сторону мгновенного поворота тела. Величину VD найдем из пропорции
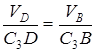 . (3)
. (3)
Чтобы вычислить C3D и С3B, заметим, что DAC3B – прямоугольный, так как острые углы в нем равны 30° и 60°, и что 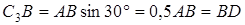 . Тогда DBC3D является равносторонним и C3B = С3D. В результате равенство (3) дает
. Тогда DBC3D является равносторонним и C3B = С3D. В результате равенство (3) дает
VD = VB = 0,46 м/c; 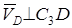 . (4)
. (4)
Так как точка Е принадлежит одновременно стержню 4, вращающемуся вокруг O2, то 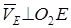 . В точках Е и D построим перпендикуляры к скоростям
. В точках Е и D построим перпендикуляры к скоростям 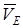 и
и 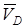 , получим точку С2 – МЦС стержня 2. По направлению вектора
, получим точку С2 – МЦС стержня 2. По направлению вектора 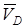 определяем направление мгновенного поворота стержня 2 вокруг центра С2. Вектор
определяем направление мгновенного поворота стержня 2 вокруг центра С2. Вектор 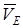 направлен в сторону поворота этого стержня. Из рис. К4б видно, что
направлен в сторону поворота этого стержня. Из рис. К4б видно, что 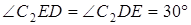 , откуда С2E=C2D. Составив теперь пропорцию, найдем, что
, откуда С2E=C2D. Составив теперь пропорцию, найдем, что
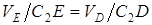 , VE = VD = 0,46 м/c. (5)
, VE = VD = 0,46 м/c. (5)
4. Определяем w2. Так как МЦС стержня 2 известен (точка С2) и 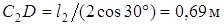 , то
, то
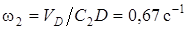 . (6)
. (6)
5. Определяем 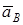 (рис. К4в, на котором изображаем все векторы ускорений). Точка B принадлежит стержню 3. Чтобы найти
(рис. К4в, на котором изображаем все векторы ускорений). Точка B принадлежит стержню 3. Чтобы найти 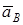 , надо знать траекторию точки B и ускорение какой-нибудь другой точки стержня 3. Такой точкой является точка A, принадлежащая еще звену 1. Следовательно,
, надо знать траекторию точки B и ускорение какой-нибудь другой точки стержня 3. Такой точкой является точка A, принадлежащая еще звену 1. Следовательно, 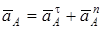 , где численно
, где численно
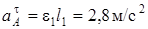 ;
; 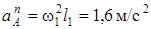 . (7)
. (7)
Вектор 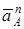 направлен вдоль AO1, а направлен вдоль AO1, а 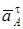 – перпендикулярно AO1; изображаем эти векторы на чертеже (см. рис. К4в). Так как точка В одновременно принадлежит ползуну, то вектор – перпендикулярно AO1; изображаем эти векторы на чертеже (см. рис. К4в). Так как точка В одновременно принадлежит ползуну, то вектор 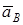 параллелен направляющим ползуна. Изображаем вектор параллелен направляющим ползуна. Изображаем вектор 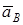 на чертеже, полагая, что он направлен в ту же сторону, что и на чертеже, полагая, что он направлен в ту же сторону, что и 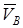 . Для определения . Для определения 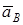 воспользуемся равенством (A – полюс): воспользуемся равенством (A – полюс): 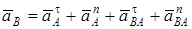 . (8) Изображаем на чертеже в точке B векторы: . (8) Изображаем на чертеже в точке B векторы: 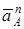 , , 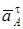 (переносное ускоре-ние точки B), (переносное ускоре-ние точки B), 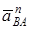 (вдоль ВА от В к А) (вдоль ВА от В к А) | 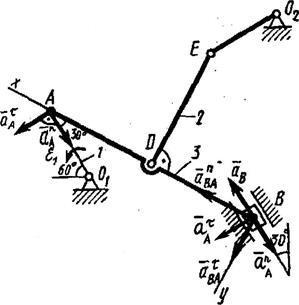 Рис. K4в Рис. K4в |
и 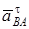 (в любую сторону перпендикулярно ВА); численно
(в любую сторону перпендикулярно ВА); численно 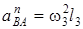 . Найдя w3 с помощью построенного МЦС C3 стержня 3, получим
. Найдя w3 с помощью построенного МЦС C3 стержня 3, получим
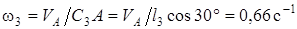 и
и 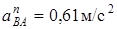 . (9)
. (9)
Таким образом, у величин, входящих в равенство (8), неизвестны только числовые значения aB и 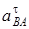 ; их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси.
; их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси.
Чтобы определить aB, спроектируем обе части равенства (8) на направление ВА (ось х), перпендикулярное неизвестному вектору 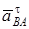 . Тогда получим
. Тогда получим
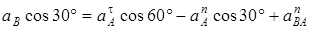 . (10)
. (10)
Подставив в равенство (10) числовые значения всех величин из (7) и (9), найдем, что
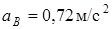 . (11)
. (11)
Так как aB>0, то вектор 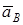 направлен, как показано на рис. К4в.
направлен, как показано на рис. К4в.
6. Определяем e3. Чтобы найти e3, сначала определим 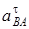 . Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим
. Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим
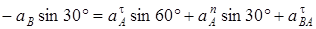 . (12)
. (12)
Подставив в равенство (12) числовые значения всех величин из (11) и (7), найдем, что 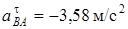 . Знак указывает, что направление
. Знак указывает, что направление 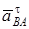 противоположно направлению, показанному на рис. К4в.
противоположно направлению, показанному на рис. К4в.
Из равенства 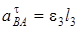 получим
получим 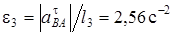 .
.
Ответ:VB =0,46 м/c; VE =0,46 м/c; w2= 0,67 c-1; 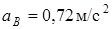 ; e3= 2,56 c-2.
; e3= 2,56 c-2.
Примечание. Если точкаВ, ускорение которой определяется, движется не прямолинейно (например, как на рис. К4.0-К4.4, где В принадлежит вращающемуся звену 4 и движется по окружности радиуса O2B), то направление 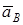 заранее неизвестно. В этом случае
заранее неизвестно. В этом случае 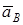 также следует представить двумя составляющими (
также следует представить двумя составляющими ( 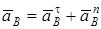 ) и исходное уравнение (8) примет вид
) и исходное уравнение (8) примет вид
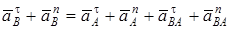 . (13)
. (13)
При этом вектор 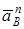 (см., например, рис. К4.0) будет направлен вдоль BO2, а вектор
(см., например, рис. К4.0) будет направлен вдоль BO2, а вектор 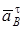 – перпендикулярно BO2 в любую сторону. Числовые значения
– перпендикулярно BO2 в любую сторону. Числовые значения 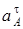 ,
, 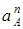 и
и 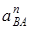 определяются так же, как в рассмотренном примере (в частности, по условиям задачи может быть
определяются так же, как в рассмотренном примере (в частности, по условиям задачи может быть 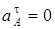 или
или 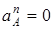 , если точка А движется прямолинейно).
, если точка А движется прямолинейно).
Значение 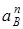 также вычисляется по формуле
также вычисляется по формуле 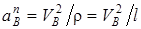 , где l – радиус окружности O2B, а VB определяется так же, как скорость любой другой точки механизма.
, где l – радиус окружности O2B, а VB определяется так же, как скорость любой другой точки механизма.
После этого в равенстве (13) остаются неизвестными только значения 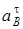 и
и 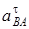 и они, как и в рассмотренном примере, находятся проектированием обеих частей равенства (13) на две оси.
и они, как и в рассмотренном примере, находятся проектированием обеих частей равенства (13) на две оси.
Найдя 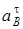 , можем вычислить искомое ускорение
, можем вычислить искомое ускорение 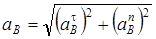 . Величина
. Величина 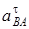 служит для нахождения eAB (как в рассмотренном примере).
служит для нахождения eAB (как в рассмотренном примере).
Вопросы для самоконтроля по кинематике
1. Векторный способ задания движения точки. Определение скорости при векторном способе задания движения точки.
2. Векторный способ задания движения точки. Определение ускорения точки.
3. Координатный способ задания движения точки. Определение траектории и скорости точки (величины и направления).
4. Координатный способ задания движения точки. Определение ускорения точки (величины и направления).
5. Естественный способ задания движения точки. Определение скорости точки.
6. Естественный способ задания движения точки. Касательное, нормальное, полное ускорения (физический смысл, величина, направление).
7. Поступательное движение твердого тела (определение). Теорема о траекториях, скоростях и ускорениях точек твердого тела. Задание движения тела.
8. Вращение твердого тела вокруг неподвижной оси (определение). Уравнение вращательного движения твердого тела вокруг неподвижной оси. Угловая скорость и угловое ускорение тела. Определение характера вращения тела.
9. Скорость и ускорение точки твердого тела, вращающегося вокруг неподвижной оси.
10.Угловая скорость тела как вектор.
11.Составное движение точки. Переносное, относительное, абсолютное движения точки (определения).
12.Составное движение точки. Переносная, относительная, абсолютная скорости точки (определения). Теорема сложения скоростей.
13.Составное движение точки. Переносное, относительное, абсолютное ускорения точки (определения). Теорема сложения ускорений в общем случае (теорема Кориолиса).
14.Определение величины и направления ускорения Кориолиса. Случаи равенства нулю ускорения Кориолиса.
15.Плоскопараллельное (плоское) движение тела (определение). Уравнения движения тела. Разложение движения на простые. Независимость угловых параметров от выбора полюса.
16.Определение абсолютной скорости точки тела методом полюса при плоском движении тела. Теорема о проекциях скоростей точек тела на прямую, проходящую через эти точки.
17.Мгновенный центр скоростей тела, совершающего плоское движение (определение). Нахождение мгновенного центра скоростей тела.
18.Мгновенный центр скоростей тела; определение абсолютной скорости любой точки тела; определение угловой скорости тела при плоском движении тела.
19.Частные случаи нахождения мгновенного центра скоростей тела при плоском движении тела.
20.Определение абсолютного ускорения точки тела методом полюса при плоском движении тела.
ДИНАМИКА
Динамика изучает движение материальных точек и механических систем с учетом сил, которые влияют на это движение.
