Линейные неоднородные уравнения второго порядка

Определение.Линейным неоднородным уравнением второго порядка называется уравнение вида

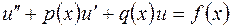. (2.14)

Решение уравнения (2.14) будем рассматривать на промежутке I непрерывности функций .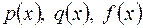

Уравнение 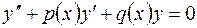(2.10) называется однородным уравнением, соответствующим уравнению (2.14).

Пусть 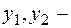два линейно независимых решения (2.10), 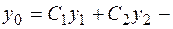общее решение (2.10), 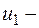частное решение ОДУ (2.14).

Свойство.Общее решение линейного неоднородного уравнения второго порядка равно сумме общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного уравнения.

Таким образом, формула общего решения уравнения (2.14) имеет вид

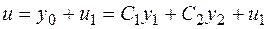. (2.14а)

Заметим, что это свойство годится для линейных неоднородных уравнений любого порядка.

Рассматривается уравнение вида

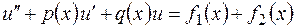. (2.15)

Лемма.(Принцип суперпозиции)

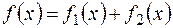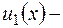Если правая часть неоднородного уравнения (2.15) есть сумма двух функций и частное решение уравнения 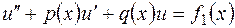, а 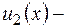частное решение уравнения 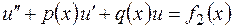,то сумма 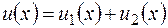есть некоторое частное решение уравнения (2.15).

Если известно общее решение 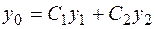соответствующего уравнению (2.14) однородного уравнения (2.10), то для определения частного решения 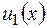уравнения (2.14) можно воспользоваться методом Лагранжа вариации произвольных постоянных.

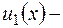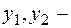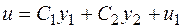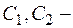Рассмотрим уравнение (2.14). Пусть какое-либо решение уравнения (2.14), а линейно независимые решения соответствующего однородного уравнения (2.10), тогда формула , где произвольные постоянные, дает общее решение уравнения (2.14).

При этом если 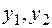известны, то решение уравнения (2.14) может быть получено по формуле:

,

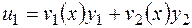где 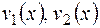определяются из системы уравнений первой степени

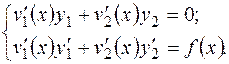(2.16)

Система (2.16) имеет единственное решение 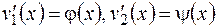, так как ее определитель – это определитель Вронского 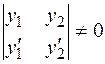. Таким образом,

.

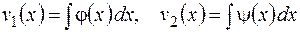Пример.Проверив, что функции 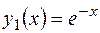, 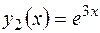образуют фундаментальную систему решений уравнения 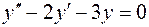, найти общее решение уравнения .

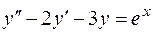Решение.Общее решение соответствующего однородного уравнения записывается в виде 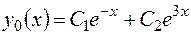. Ищем частное решение уравнения 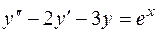по формуле 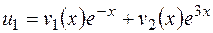. Для определения 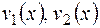составим систему вида (2.16)

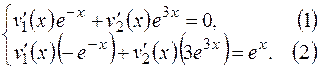
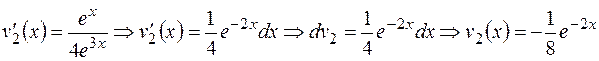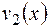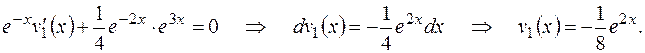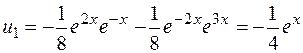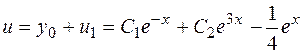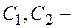Сложив уравнения (1) и (2), получим . Подставив найденное в (1), будем иметь Итак, . Общее решение уравнения имеет вид , где произвольные постоянные.

2.3.4. Примеры для самостоятельного решения

1. Исследовать на линейную зависимость следующие системы функций:

а) 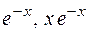; б) .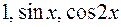

2. Проверив, что функция 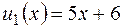является частным решением уравнения 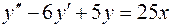, а функция 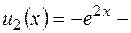частным решением уравнения 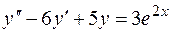, найти общее решение уравнения .

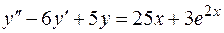3. Проверив, что функци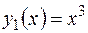и и 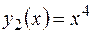образуют фундаментальную систему решений уравнения 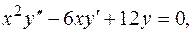найти общее решение уравнения .

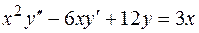Линейные однородные уравнения с постоянными

Коэффициентами

Общий вид линейного дифференциального уравнения порядка 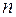с постоянными коэффициентами есть

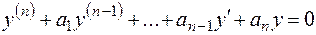, (2.17)

где 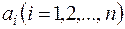- действительные постоянные.

Определение.Уравнение

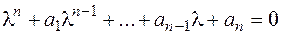, (2.18)

полученное заменой производных 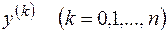искомой функции степенями 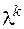, называется характеристическим уравнением для уравнения (2.17).

Каждому действительному корню 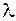уравнения (2.18) кратности 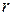соответствуют 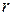линейно независимых решений уравнения (2.17)

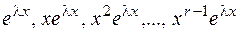, (2.19)

а каждой паре комплексных корней 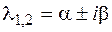кратности 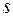соответствуют 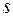пар линейно независимых решений:

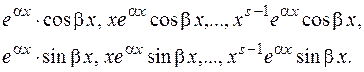(2.20)

Запишем общее решение для случая 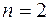. Рассмотрим уравнение

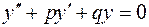, (2.21)

где 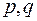- действительные числа.

Характеристическое уравнение для (2.21) имеет вид

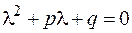. (2.22)

Если квадратное уравнение (2.22) имеет два различных действительных корня 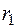и 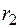, то согласно (2.19) имеем два линейно независимых решения уравнения (2.21)

.

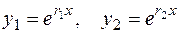Общее решение имеет вид

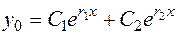, (2.23)

где 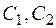- произвольные постоянные.

Если квадратное уравнение (2.22) имеет комплексные корни 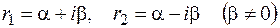, тогда согласно (2.20) имеем два линейно независимых решения уравнения (2.21)

.

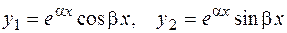Общее решение имеет вид

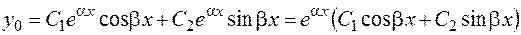. (2.24)

Если квадратное уравнение (2.22) имеет два равных действительных корня 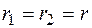, то согласно (2.19) имеем два линейно независимых решения уравнения (2.21)

.

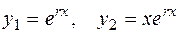Общее решение уравнения имеет вид

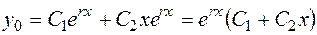. (2.25)

Примеры. Найти общее решение уравнений:

1. ;

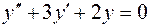2. ;

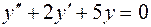3. .

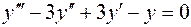Решения.

1. Рассмотрим 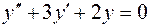, его характеристическое урав-нение 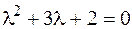имеет корни 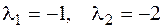. Запишем фундаментальную систему решений 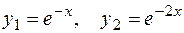. Следовательно, общее решение имеет вид .

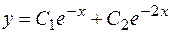2. Для уравнения 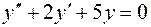характеристическое уравне-ние имеет вид 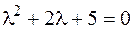, его корни 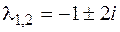. Следовательно, функции 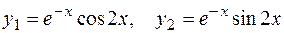составляют фундаментальную систему решений, а общее решение имеет вид .

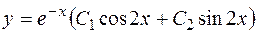3. Уравнение 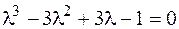является характеристичес-ким для 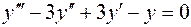, его решением является 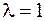кратности 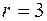. Поэтому фундаментальная система решений имеет вид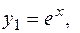 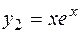, 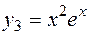. Следовательно, общее решение исходного уравнения имеет вид:

.

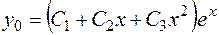2.3.6. Примеры для самостоятельного решения

Найти общие решения дифференциальных уравнений.

1. 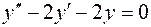,	4. ,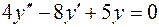
2. 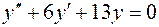,	5. ,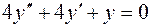
3. 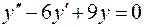,	6. 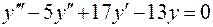.