Расчет статически неопределимой рамы методом перемещений

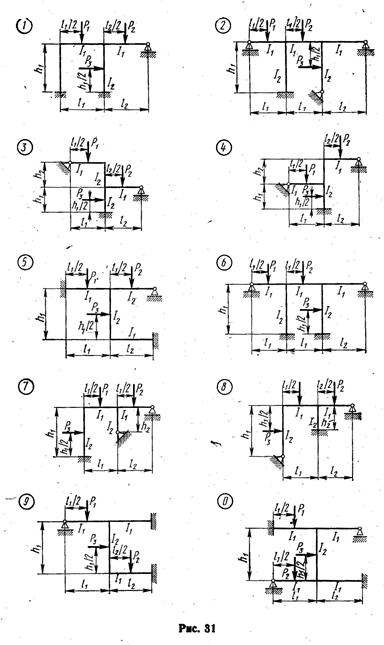
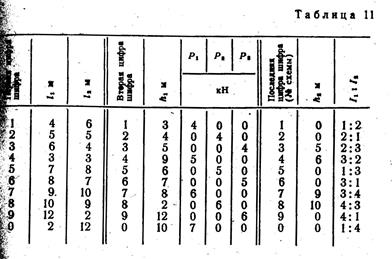
Задание. Для заданной статически неопределимой рамы (рис. 31) с выбранными по шифру из табл. 11 размерами и нагрузкойтребуется построить эпюры изгибающих моментов, поперечных и продольных сил.

Методические указании

Решению задачи должно предшествовать изучение темы 10. При выборе основной системы метода перемещений необходимо учитывать, что линейные связи должны быть поставлены не только по направлению возможных линейных перемещений, но и для устранения мгновенной изменяемости системы, образованной после постановки шарниров во все узлы (включая опорные).

При построении единичных и грузовых эпюр моментов используются таблицы реакций, имеющиеся в учебниках.

Прежде чем приступать к подсчету коэффициентов канонических уравнений, необходимо значения ординат на всех единичных эпюрах выразить через какую-либо одну жесткость (El1 или El2). Удобно также перейти к погонным жесткостям стержней (i=EI:l). При определении коэффициентов следует внимательно следить за ихзнаками, а также использовать теорему о взаимности реакций. Решением системы канонических уравнений необходимо прове­рить.

После определения значений неизвестных рекомендуется постро­ить эпюры моментов ( 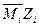). Суммирование этих эпюр между собой и с грузовой эпюрой дает окончательную эпюру моментов. Суммирование рекомендуется производить по характерным точкам и в пояснениях обязательно приводить все расчеты.

Эпюры поперечных и продольных сил строятся по эпюре моментов так же, как и в задаче 7.

Проверку полученных эпюр надо проводить как статическую (равновесие узлов и рамы в целом), так и кинематическую. Для последней проверки необходимо выбрать основную систему метода сил и построить хотя бы одну единичную эпюру, которую следует «умножить» на окончательную эпюру моментов по правилу Верещагина.

Расчет плоской рамы на устойчивость

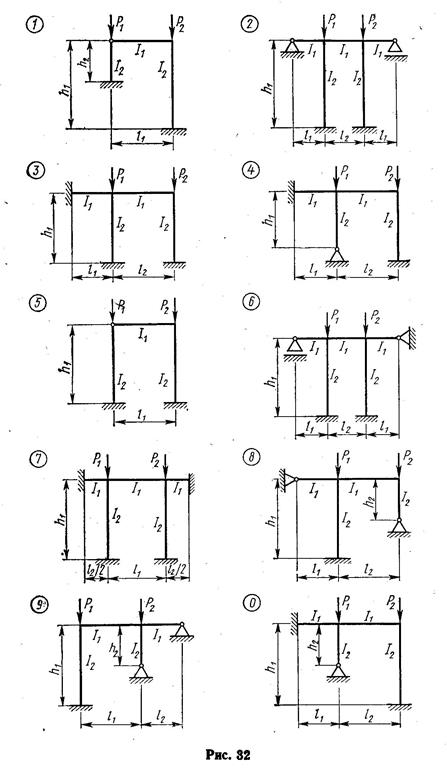
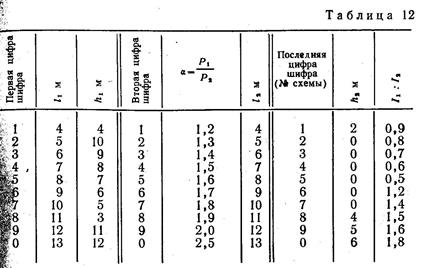
Задание.Для статически неопределимой рамы (рис. 32) с вы­данными по шифру из табл. 12 размерами и нагрузкой требуется определить значения критических сил, используя метод переме­щений.

Методические указания

Решению задачи должно предшествовать изучение тем 18—23.

Все предлагаемые рамы целесообразно решать методом переме­щений. Так как внешние нагрузки действуют вдоль стоек, то грузовых эпюр в основной системе не будет и свободные члены канони­рских уравнений обратятся в нуль.

Построение единичных эпюр для сжатых силами стоек следует проводить по специальным таблицам, а для ригелей — по обычным таблицам метода перемещений. Специальные таблицы, необходимые функции и их значения для метода перемещений можно найти в пособии А. Ф. Смирнова «Таблицы функций для расчета стержневых систем на устойчивость и колебания», табл. 2 (изд. МИИТ, 1965). Такие же таблицы можно найти и в источниках [13], [15], [16], 17].

Коэффициенты канонических уравнений будут включать в себя некоторые функции ( 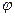_n(vi) и ( 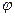_m(vk) от параметров

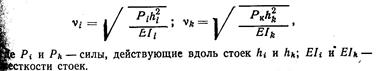
По заданию силы Pi и Рk. связаны между собой соотношением поэтому и параметры Vi и Vk окажутся связанными соотношением:

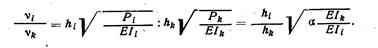
Для нахождения Р_кр составляется уравнение устойчивости

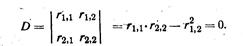
Это уравнение решается относительно v подбором в такой по­следовательности: а) задаются значением vk; б) по вычисленному соотношению определяется vi; в) по таблицам находятся значения необходимых коэффициентов (функций 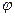n(vi), 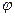_m(vk)..); г) най­денные значения функций подставляются в уравнение устойчивости.

Если данные значения функций не удовлетворяют уравнению устойчивости, то задаются другим значением vkи все вычисления повторяются. Эта операция продолжается до тех пор, пока приня­тые значения не будут удовлетворять уравнению устойчивости. Тогда по формулам

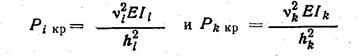
определяются значения критических сил.