Выбор модели и ее исследование

При планировании и реализации экспериментов вид поверхности отклика и описывающей ее функции, как правило, неизвестен. Поэтому реальная функция отклика аппроксимируется алгебраическим полиномом, полученным при разложении неизвестной функции отклика в ряд Тейлора в окрестности любой точки из области определения этой функции в факторном пространстве. Тогда:

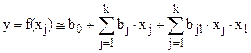, j ¹ l ,(6.24)

где b – коэффициенты; x – факторы.

По результатам экспериментальных исследований коэффициенты регрессионной модели определяются методом наименьших квадратов – регрессионным анализом. Модель всегда линейна относительно коэффициентов (не переменных факторов).

При однофакторных экспериментах модель может быть интерпретирована геометрически в виде кривой на плоскости; при двух факторах – это поверхность в пространстве; при трех и более факторах модель может быть представлена только отдельными ее сечениями.

Оценка коэффициентов модели должна быть состоятельной, несмещенной, эффективной и достаточной. Рассмотрим это подробнее.

Оценка состоятельна, если при увеличении объема выборки она приближается к истинной величине; не смещена, если ее математическое ожидание равно оцениваемому коэффициенту; эффективна, т.е. имеет минимальную дисперсию, и достаточна, если включает максимум информации о коэффициенте.

При постановке оптимизационных задач для движения по поверхности отклика к экстремуму необходимое направление может быть выбрано по линейной модели. В этом случае экстремум достигается пошаговым приближением экспериментов к зоне оптимума.

Если зона экстремума априорно известна, и необходимо выяснить, например, допустимый разброс переменных факторов, то используют метод перевала. При этом всю зону факторного пространства дробят на два блока: до и после экстремума. В каждом блоке ставят отдельный факторный эксперимент и получают две линейные модели.

Надежное предсказание поведения исследуемого объекта при помощи модели возможно только при ее адекватности. Модель адекватна, если ее погрешность не превышает погрешности экспериментов, на основании которых она получена.

Следует отметить, что интерполяционные модели удобнее выражать через натуральные значения факторов, а оптимизационные – через кодовые. Исследование полученных моделей также удобнее выполнять в кодовых переменных.

Рассмотрим процедуру канонического анализа математической модели в виде полинома второго порядка. Задача сводится к преобразованию квадратичного полинома к выражению канонического вида

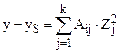, (3. 11)

где y – текущее значение параметра оптимизации; y_S – значение в новых координатах; A_ij – коэффициенты уравнения регрессии канонического вида при квадратичных членах; Z_j – новые оси координат (смещенные в новый центр и повернутые относительно старых осей).

Геометрическая интерпретация канонического преобразования уравнения поверхности отклика представлена на рис. 3.6.

Следует отметить, что при числе факторов k ³ 3 канонические преобразования усложняются, и в этих случаях целесообразно использовать методы матричной алгебры.

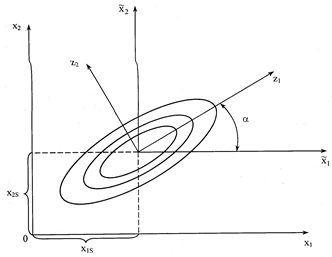Рис. 3.6. Схема канонических преобразований

Поиск оптимума

Исследователями Кифером и Вольфовичем (США) был предложен градиентный метод оптимизации, предназначенный для шагового движении к экстремуму поверхности отклика в задачах оптимизации.

Градиент функции представляет собой вектор, показывающий наискорейшее изменение функции, величина и направление которого определяются по формуле

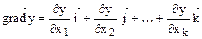, (3. 12)

где y – выход эксперимента; x_k – переменные факторы; 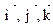– единичные векторы по соответствующим координатам.

Наиболее просто значение производной может быть оценено как отношение приращения функции к приращению отдельных факторов при реализации двух экспериментов, поставленных в окрестностях исходной точки факторного пространства: пробного и рабочего опытов, например, в направлении фактора x₁. Тогда

.

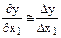Ставя последовательно несколько опытов вокруг пробной точки, определяют составляющие градиента по осям факторного пространства, т.е. направление движения к оптимуму. Кроме того, задаются величиной рабочего шага при этом движении.

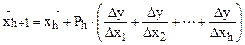, (3.13)

где P – параметр рабочего шага; h – номер шага.

Геометрическая интерпретация движения к оптимуму методом градиента представлена на рис. 3.7.

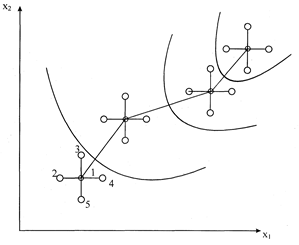Рис.3.7. Схема движения к оптимуму методом градиента (цифры на точках номера опытов)

Из целого ряда градиентных методов наиболее широкое применение получил метод “крутого восхождения”, предложенный Боксом и Уилсоном в 1951 году. Этот метод определяет стратегию последовательного пошагового проведения экспериментов, при котором весь цикл исследований разбивается на отдельные этапы. Причем на каждом последующем этапе используются результаты предыдущего.

Согласно теореме Тейлора о разложении аналитической функции в ряд, частные производные функции по факторам равны по величине и знаку соответствующим коэффициентам линейного уравнения регрессии.

Следовательно,

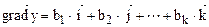( 3. 14)

и 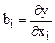. ( 3. 15)

Рассмотрим формализованную процедуру крутого восхождения с численным приме-ром.

В начале необходимо иметь линейную модель, построенную по результатам эксперимента, и знать интервалы варьирования и нулевой уровень факторов.

Дано: адекватная линейная модель в кодовых переменных:

h = 41 + 10x₁ + 6x₂ – 5x₃ – 4x₄ .

Известно, что x₄ является качественным фактором (например, конструкцией узла) и наилучшие результаты дает конструкция с кодовым значением “–1”. При крутом восхождении это значение качественного фактора фиксируется и модель приобретает вид

h = 45 + 10x₁ + 6x₂ – 3x₃ .

Если оба уровня качественного фактора дают близкие результаты, то крутое восхож-дение повторяется на двух уровнях. Интервалы варьирования факторов в натуральных переменных:

Dx₁ = ±0,15; Dx₂ = ±100; Dx₃ = ±50;

нулевой уровень факторов:

x_0,1 = 0,4; x_0,2 = 840; x_0,3 = 60.

1. Выбор базового фактора.

В качестве базового рекомендуется выбирать фактор с наибольшей абсолютной величиной коэффициента линейной модели или фактор с наибольшим интервалом варьирования.

Пример.

Выбираем в качестве базового фактор x₂, так как

|b₁| > |b₂| > |b₃| и Dx₂ > Dx₃ > Dx₁.

2. Выбор шага базисного фактора.

Величины шагов движения по факторным осям должны быть больше ошибки, с которой фиксируется фактор. Малый шаг увеличивает количество опытов, а слишком большой – может привести к проскоку экстремума.

Обычно шаг P_j выбирают в долях m интервала варьирования фактора:

P_j = m×Dx_j, ( 3. 16)

где 0 < m < 1.

Пример.

Р_б = Р₂ = 0,2×100 = 20.

3. Расчет шагов для остальных факторов выполняем по формуле

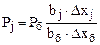, ( 3. 17)

где индекс “б” относится к базовому фактору.

Пример.

; .

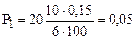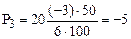При необходимости шаги можно для удобства счета округлять.

4. Выбор начала движения по градиенту.

За начало движения по градиенту функции отклика можно брать любую точку поверхности отклика. Обычно используют центр эксперимента (основной или нулевой уровень каждого фактора). Но если есть предположение о наличии экстремума в некоторой точке, то эту точку нужно брать в вилку.

Пример: в качестве начала движения выбираем основной уровень.

5. Расчет величин факторов для первого шага:

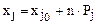, ( 3.18 )

где n – порядковый номер шага.

Пример.

x₁ = 0,4 + 1×0,05 = 0,45; x₂ = 840 + 1×20 = 860; x₃ = 60 + 1×(–5) = 55.

6. Перевод натуральных значений факторов для первого шага движения в кодовые.

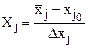, ( 3. 19)

где 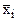– натуральное значение фактора.

Пример.

; ; .

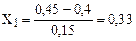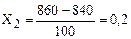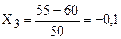7. Расчет выхода в первом мысленном опыте.

Пример.

y₉ = 45 + 10×0,33 + 6×0,2 – 3×(–0,1) = 49,2

8. Повторить этапы 5, 6, 7. Результаты сведены в табл. 3.1.

Таблица 3.1

Реализация реальных и мысленных экспериментов

Номер опыта	Факторы	Выход	Примечание
натуральные	кодовые
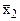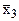			X1	X2	X3
	0,55			+1	+1	+1		ДФЭ 24–1 для построения линейной модели
	0,25			–1	+1	+1
	0,55			+1	–1	+1
	0,25			–1	–1	+1
	0,55			+1	+1	–1
	0,25			–1	+1	–1
	0,55			+1	–1	–1
	0,25			–1	–1	–1
	0,45			0,33	0,2	–0,1	49,2	Мысленные опыты
	0,50			0,67	0,4	–0,2	53,5
	0,55				0,6	–0,3	62,71	Реальный опыт
	0,60			1,33	0,8	–0,4	64,3	Мысленные опыты
	0,65			1,67		–0,5	69,2
	0,70				1,2	–0,6	75,17	Реальные опыты
	0,75			2,33	1,4	–0,7	69,21

После каждых одного-трех мысленных опытов следует ставить один реальный с тем же шагом для проверки. Обнаружив оптимум, необходимо поставить один или два (с двух сторон от экстремума) реальных опыта для подтверждения наличия оптимума. В процессе движения по градиенту экстремум может быть как внутри интервалов варьирования факторов, так и вне их, т.е. допускается некоторая экстраполяция экспериментальной области.

Если один из факторов при движении по градиенту достиг своих физических пределов и дальше изменяться не может, то необходимо, фиксировав его на этом предельном уровне, двигаться, меняя оставшиеся факторы.

Крутое восхождение прекращают, если найден оптимум или если ограничения по факторам делают движение по градиенту нефизичным (нереальным).

Следует иметь в виду, что, сокращая общее число опытов для достижения экстремума, метод крутого восхождения не позволяет обнаружить экстремум одними мысленными опытами (уравнение регрессии линейно); он указывает лишь на кратчайший путь к оптимуму.