Весовая нагрузка рамы тележки

Вертикальные силы веса, действующие на раму тележки, составляют

- собственный вес рамы;

- вес тормозного оборудования;

- вес подрессоренной части тягового двигателя;

- передачи и системы первичного подвешивания;

- части веса кузова, приходящиеся на тележку.

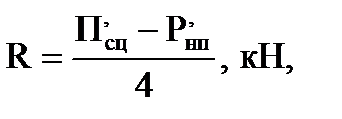Величина реакций рессорных подвесок определяем в кН из условия

где Р′_нп - вес неподрессоренных частей, отнесенных к одной кп , кН

4 - четыре точкикрепления;

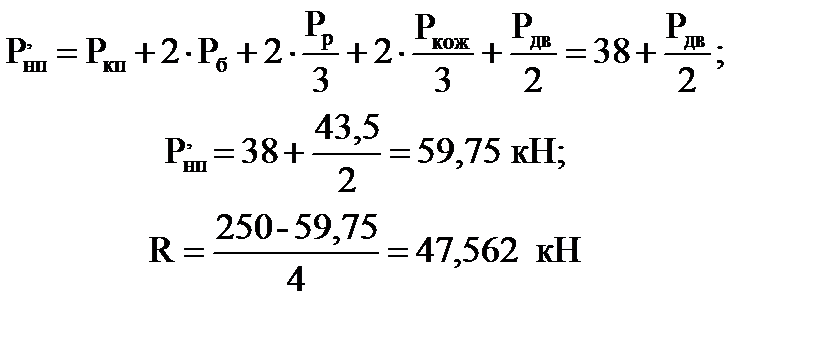
Нагрузка от веса кузова, приходящаяся на одну тележку

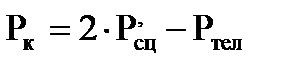
где Р_тел - вес одной тележки электровоза кН

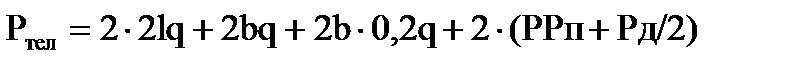
где

q – интен- сивность равномерно распределенной нагрузки .

Сосредоточенная нагрузка от веса кузова электровоза

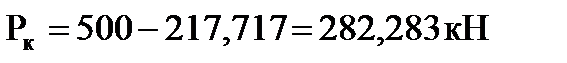
Напряжение в опасном сечении рамы тележки от весовойнагрузки

Рассчитаем изгибающий момент в заделке и построим эпюру

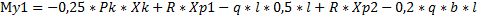
My1= - 0,25*282,283*0,59+47,562*0,875 – 4,4632*2,405*0,5*2,405+47,562*2,275 – 0,2*4,4632*1,1*2,405=92,915кН*м

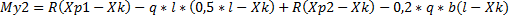
My2= 47,562(0,875 – 0,59) – 4,4632*2,405(0,5*2,405 – 0,59) + 47,562(2,275 – 0,59) -0,2*4,4632*1,1(2,405 - 0,59) =85,34 кН*м

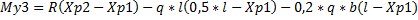
My3=47,562(2,275 – 0,875) – 4,4632*2,405(0,5*2,405 – 0,875) – 0,2*4,4632*1,1(2,405 – 0,875) = 61,569кН*м

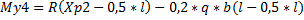
My4 =47,562( 2,275 – 0,5*2,405) – 0,2*4,4632*1,1(2,405 – 0,5*2,405) = 49,83 кН*м

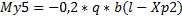
My5 = -0,2 *4,4632*1,1(2,405 – 2,275) = -0,127 кН*м

Определим напряжение для точки 1:

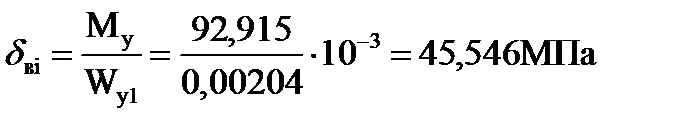
так как 1 H/mm² = 1 МПа.

Рисунок4. Расчетная схема и эпюра изгибающих моментов

Допустимая скорость движения локомотива в кривой

Для определения допустимой скорости движения в кривой решим систему уравнений равновесия сил, действующих на тележку (рисунок 5)

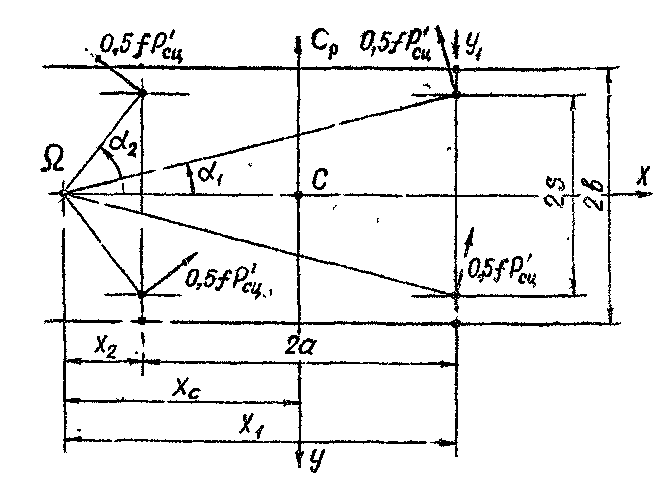
Рисунок 5. Схема сил, действующихна тележку при движении в кривой

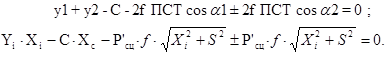
где Yi - направляющее усилие первой по ходу колесной пары, кН;

С - значение непогашенной центробежной силы для

массы электровоза, приходящейся на тележку, кН ;

f - коэффициент трения между колесом и рельсом.

t ∙ Р'сц ∙Cos(αi) – проекция силы трения на ось Y .

Величина допустимой скорости движения в кривой без возвышения:

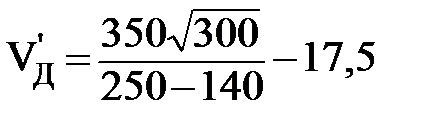=37,61 км/ч.

Скорость движения в кривой без возвышения наружного рельса:

;

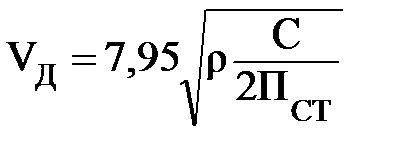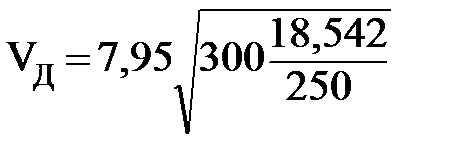=37,5 км/ч.

Определим центробежную силу:

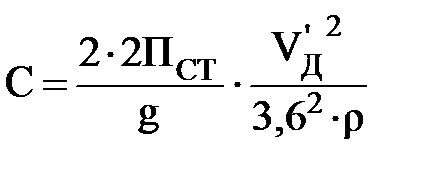, кН;

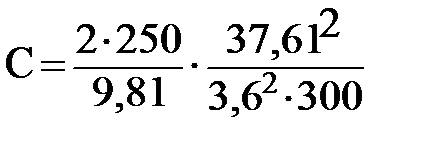=18,542 км/ч.

С возвышением наружного рельса:

;

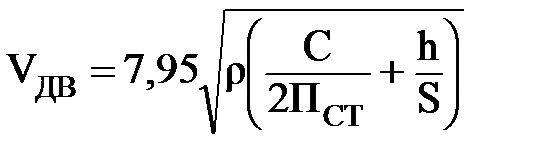где h - возвышение наружного рельса в кривой, м;

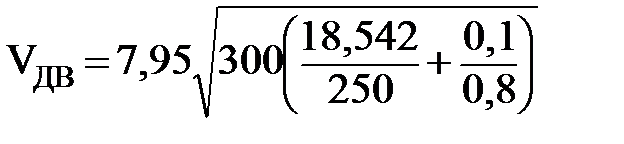=61,452км/ч.

Зададимся диапазоном возможных значений х_с от х_min= 1 м до х_max = х_снп 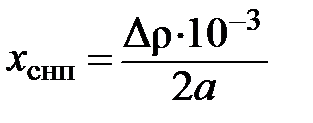(м):

, м,

где ρ – заданный радиус кривой, м;

∆ - суммарный зазор для колесной пары в кривой радиуса=300, мм.

∆=24 мм,

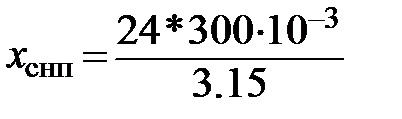=2,285 м.

Значит, 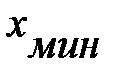= 1 м,а 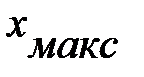= 2,285 м.

Силы, действующие на раму тележки, при движении

Электровоза в кривой

Полную систему сил, действующих на раму тележки, при движении в кривой можно рассмотреть как состоящую из двух независимых систем.

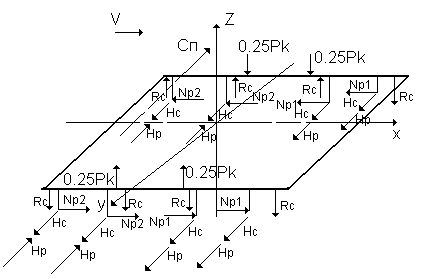
Рисунок 6 - Схема действия сил на раму тележки при движении в кривой

Величина центробежной силы подрессоренных масс С_П в кН, отнесенной к одной тележке определяем для допустимой скорости V_Д для кривой без возвышения наружного рельса по формуле

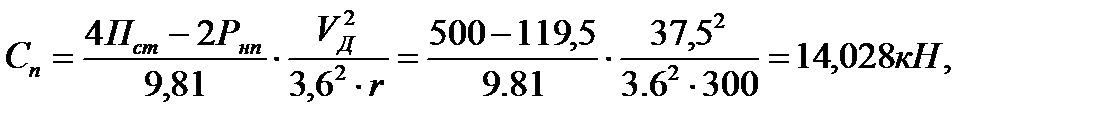
где r - радиус кривой.

Перераспределение вертикальных реакций:

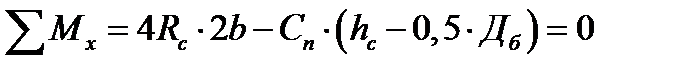
h_c= 2,2 м

где h_c - высота центра тяжести подрессоренных масс, относительно УГР;

b - половина ширины рамы тележки;

Д_б= 1,25м - расчетный диаметр колес по кругу катания.

Из этого уравнения определяем перегрузку R_c

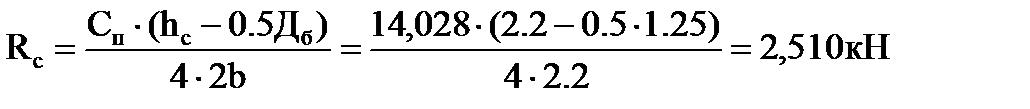
Горизонтальные реакции, приложенные к буксовым кронштейнам, принимаем равными между собой и определяем

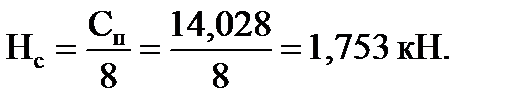
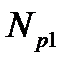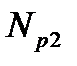Принудительный поворот тележки без качения колес приводит к проскальзыванию бандажей. Со стороны колесной пары на боковины рамы действуют силы и , определяемые как

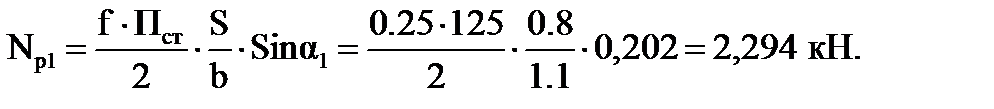
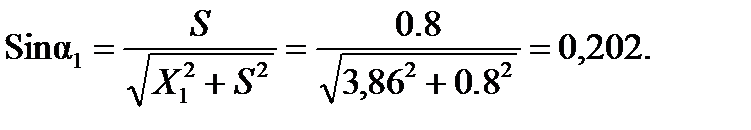
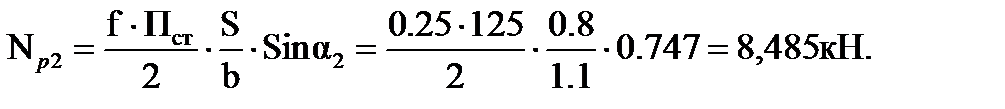
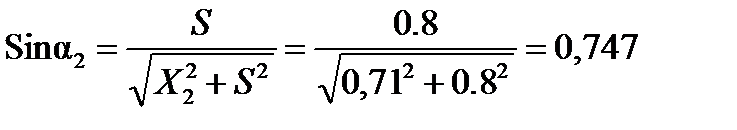
При допустимой скорости движения в кривой V_д = 37,5 км/ч,

x₁ = 3,86 м; x₂ = 0,71 м; S= 0,8 м; f= 0,25.

Продольные усилия стремятся повернуть раму тележки в горизонтальной плоскости, этому препятствуют буксы, закрепленные на шейках осей колесных пар. В результате появляются поперечные горизонтальные реакции H_p, приложенные к буксовым направляющим. Величина H_p рассчитывается из условия равновесия от действия этих сил и выражается уравнением

;

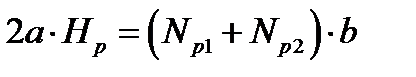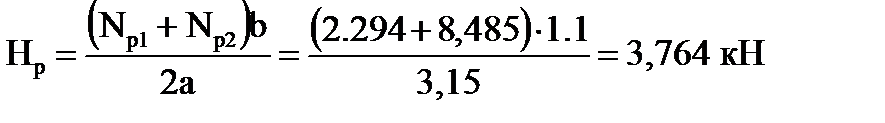
7. Напряжения в опасном сечении при движении локомотива

В кривой

Система сил R_c, H_c, N_p, H_p, создает в заделке консоли два изгибающих момента: момент М_х действующий в вертикальной плоскости, и момент M_z действующий в горизонтальной плоскости (рисунок 7).

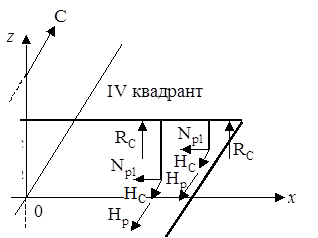
Рисунок 7 – Схема сил, действующих на раму тележки при движении в кривой.

Составим уравнения для определения изгибающих моментов в опасном сечении рамы в вертикальной плоскости xoy.

M_y1 =Rc*Xp1+Rc*Xp2 – Np1*Zn1 – Np1*Zn2 = 2,51*0,875+2,51*2,275 – 2,294*0,475–2,294*0,275=6,187кН*м

M_y2 = - Rc*Xp1+Rc*Xp2 – Np1*Zn1 – Np1*Zn2= - 2,51*0,875+2,51*2,275 – 2,294*0,475 – 2,294*0,275 = 1,795кН*м

M_y3 = -R_c*Xп1+Rc*Xp2 – Np1*Zn1- Np1*Zn2 = -2,51*1,1+2,51*2,275 – 2,294*0,475 – 2,294*0,275= 1,23кН*м

M_y4 = Rc(Xp2 – Xn2) = 2,51(2,275 – 2,05) = 0,564кН*м

M_у5 = 0

M_z1 = (Нс+Нр)*(Хп1+Хп2) = (1,753+3,764)*(1,1+2,05) = 17,378кН*м

Мz2= (Нс+Нр)*(Хп1-Хп2) = (1,753+3,764)*(1,1 – 2,05) = -5,241кН*м

Мz3= (Нс+Нр)*Хп2 = 11,309кН*м

Мz4= (Нс+Нр)*Xп1= 6,068кН*м

Mz5=0

Определим напряжение изгиба относительно осиy:

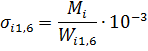
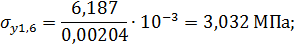
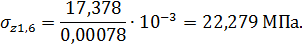
Суммарное напряжение изгиба в расчетных точках 1 и 6

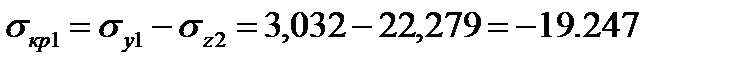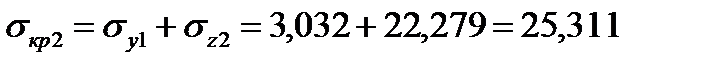МПа.

МПа.

На основании полученных данных заполним таблицу 4.

Таблица 4 – Напряжение в расчетных точках 1и 6

Точки сечения
Напряжение от изгиба относительно оси у , МПа	3,032	3,032
Напряжение от изгиба относительно оси z, МПа	22,279	-22,279
Суммарные напряжения, МПа	25,311	-19,247

Изобразим эпюры изгибающих моментов (рисунок 7)

Рисунок 7 – Расчетная схема и эпюра изгибающих моментов