Лекция 9 плоские задачи теории фильтрации об установившемся притоке к скважине

При разработке нефтяных и газовых месторождений возникает два вида задач:

1. Задаётся дебит скважин и требуется определить необходимое для этого дебита забойное давление и давление в любой точке пласта. В данном случае величина дебита определяется значением предельной для имеющихся коллекторов депрессией, при которой ещё не наступает их разрушение, или прочностными характеристиками скважинного оборудования.

2. Задаётся забойное давление и требуется определить дебит, что часто встречается в практике разработки. Величина забойного давления определяется условиями эксплуатации. Например, давление должно быть больше давления насыщения для предотвращения дегазации нефти в пласте или больше давления, при котором выпадает конденсат в пласте, при разработке газоконденсатных месторождений. Если возможен вынос песка из пласта на забой скважины, то скорость в скважине должна быть достаточной для его выноса на поверхность.

Рисунок 9.1 – Зависимость суммарного дебита от числа скважин

При эксплуатации группы скважин в одинаковых условиях, т. е. с одинаковым забойным давлением, дебит всего месторождения растёт медленнее увеличения числа скважин (рисунок 9.1).

Для решения поставленных задач решим задачу плоской интерференции (взаимодействия) скважин. Предположим, что пласт – неограниченный, горизонтальный, имеет постоянную мощность и непроницаемые подошву и кровлю. Он вскрыт совершенными скважинами и заполнен однородной жидкостью или газом. Движение жидкости – установившееся, подчиняется закону Дарси и является плоским. Плоское движение означает, что течение происходит в плоскостях, параллельных между собой и картина движения во всех плоскостях идентична. В связи с этим разбирается течение в одной из этих плоскостей – в основной плоскости течения.

Решение задач будем строить на принципе суперпозиции (наложения) потоков, который заключается в следующем. При совместном действии в пласте нескольких стоков (эксплуатационных скважин) или источников (нагнетательных скважин) потенциальная функция, определяемая каждым стоком (источником), вычисляется по формуле для единственного стока (источника).

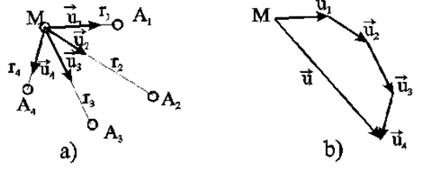
Рисунок 9.2 – Схема скоростей фильтрации в точке М при работе источников и стоков на неограниченной плоскости (а) и результирующий вектор скорости фильтрации в точке М (b)

Потенциальная функция, обусловленная всеми стоками (источниками), вычисляется алгебраическим сложением этих независимых друг от друга значений потенциальной функции. Суммарная скорость фильтрации определяется как векторная сумма скоростей фильтрации, вызванная работой каждой скважины (рисунок 9.2b).

Пусть в неограниченном пласте действует n стоков с положительным массовым дебитом G и источников с отрицательным дебитом (рисунок. 9.2a). Поток вблизи каждой скважины в этом случае плоскорадиален и потенциал запишется :

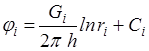, (9.1)

где i – номер скважины; r_i– расстояние между некоторой точкой пласта и центром скважины под номером i.

Пользуясь методом суперпозиции, определим потенциал сложного потока:

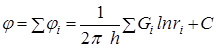, (9.2)

где .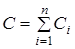

Формула (9.2) основная в решении задач интерференции скважин.

Зависимость (9.2) физически означает, что фильтрационные потоки от работы каждого источника-стока накладываются друг на друга.

Если жидкость несжимаема, то вместо массовых дебитов можно использовать объёмные дебиты Q в зависимости (9.2).

Для определения уравнений эквипотенциальных поверхностей (изобар) следует иметь в виду, что во всех точках этих кривых значение потенциала (давления) должно оставаться неизменным. Таким образом, приравнивая (9.2) к некоторой постоянной, получим:

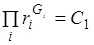, (9.3)

где П – знак произведения; С₁– постоянная.

Если дебиты всех скважин равны по величине, то:

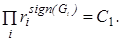(9.4)

Линии тока образуют семейство кривых, ортогональных изобарам.

Метод суперпозиции можно использовать не только в бесконечных пластах, но и в пластах, имеющих вблизи скважин контур питания или непроницаемую границу. В этом случае для выполнения условий на границах вводятся фиктивные стоки или источники за пределами пласта. Фиктивные скважины в совокупности с реальными обеспечивают необходимые условия на границах и задача сводится к рассмотрению одновременной работы реальных и фиктивных скважин в неограниченном пласте. Данный метод называется методом отображения источников и стоков.