Связь плоской задачи теории фильтрации с теорией функций комплексного переменного

При исследовании плоского фильтрационного потока, подчиняющегося закону Дарси, можно использовать теорию функций комплексного переменного. Совместим плоскость комплексного переменного z= x +iy с основной плоскостью течения.

Для каждого плоского фильтрационного потока можно найти характеристическую функцию течения, или комплексный потенциал F(z), который является функцией комплексного переменного z. В функции F(z) можно отделить действительную часть от мнимой:

F(z)= Ф(х,у) + iψ(x,y), (5.50)

где Ф(х,у) - потенциал скорости; ψ(x,y) - функция тока. Эти функции связаны между собой уравнениями Коши -Римана:

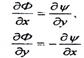(5.51)

и подчиняются уравнению Лапласа:

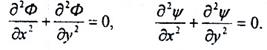(5.52)

Уравнение Ф(х,у)=c определяет собой семейство эквипотенциалей,

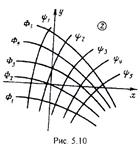
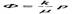совпадающих с изобарами, так как , а ψ(x,y) = с – семейство

линий тока. Эквипотенциали и линии тока взаимно ортогональны (рис.5.10).

Проекции скорости фильтрации на координатные оси находятся по формулам:

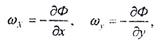(5.53)

а модуль скорости фильтрации

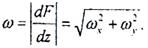(5.54)

Время движения частицы жидкости вдоль линии тока s можно определить по формуле

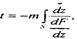(5.55)

где z = x-iy - сопряженное с z комплексное переменное.

Если какой-либо сложный плоский фильтрационный поток можно

представить как результат наложения нескольких простейших потоков, то характеристическая функция сложного потока равна по принципу суперпозиции алгебраической сумме характеристических функций простейших потоков.

Задача 15

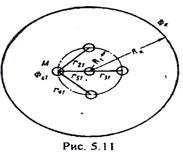Определить дебит батареи из четырех скважин, расположенных вдали от контура питания, и одной скважины, находящейся в центре (рис.5.11), если известно, что все скважины находятся в одинаковых условиях; радиус батареи R1=200 м, расстояние до контура питания Rk⁼10 км, радиус скважины r_с=0,1 м, толщина пласта h=10 м, потенциал на контуре питания Ф_к=40 см²/с, потенциал на скважинах Ф_с=30 см²/с.

Решение.Будем исходить из формулы для потенциала при работе группы скважин:

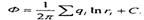(5.56)

Учитывая, что скважины расположены вдали от контура питания, в точке, помещенной на контуре питания, получим

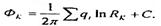(5.57)

Помещая точку М на забой первой скважины и учитывая, что q1=q2=q3=q4

будем иметь

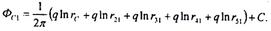(5.58)

Вычитая из (5.57) и заменяя (см. рис.5.11)

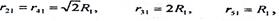
получим

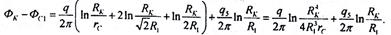(5.59)

Помещая точку М на забой центральной скважины, определим Ф_С5:

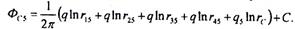(5.60)

Вычитая из (5.57) (5.60) и учитывая, что

^r15 ^=r 25 ^=r 35^{= r} 45 ⁼R1

получим

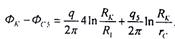
Подставив в (5.59) и (5.60) исходные данные:

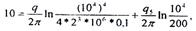
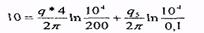
и решив полученную систему уравнений относительно q и q , найдем:

q = 2,2Scм²/c, q₅==l,95cм²/c, Q = qh = 2,28*10³ см³/с = 197 м³/сут,

Q₅ = qbh= 1,95*10³см³/с = 168 м³/сут., найдем:

Задача 1 6

Круговой нефтяной пласт радиусом R_K=15 км, толщиной h=8 м эксплуатируется пятью скважинами радиусом r_с=7,5 см, из которых четыре расположены в вершинах квадрата со стороной d=150 м, а пятая - в центре (см. рис.5. 11). Контурное давление р_к=10,78 МПа, скважины работают с одинаковым забойным давлением рс= 8,82 МПа.

Коэффициент проницаемости пласта k=0,6 мкм2, динамический коэффициент

вязкости нефти μ=1,1 мПа*с.

Определить дебиты скважин и отношение дебитов

Задача 1 7

Найти значения потенциалов на скважинах, расположенных симметрично на расстоянии 2 σ =300 м относительно центра кругового контура питания радиуса

R_K ⁼5 км, если известно, что дебит одной составляет 200 т/сут, а другой - 300 т/сут, потенциал на контуре питания Фк=50 см²/с, радиус скважины rc⁼0, 1 м, толщина пласта h= 1 0 м, плотность нефти ρ=850 кг/ м³.

Указание.Считать, что контур питания одинаково удален от каждой из интерферирующих скважин.

Задача 18

Определить, при каком постоянном забойном давлении работала скв. 1 с радиусом rс=0,1 м в круговом пласте радиуса R_K =10 км, если при введении скв. 2 с таким же радиусом, расположенной на расстоянии 2σ = 150 м от первой и работающей с забойным давлением рс2=6,82 МПа, скв. 1 была полностью заглушена. Давление на контуре питания рк= 9,8 МПа.

Решение.Считая скважины достаточно удаленными от контура питания и применяя принцип суперпозиции, запишем выражение для потенциала результирующего течения в произвольной точке М (рис.5. 12).

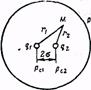
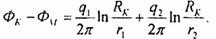
Помещая точку М на контур первой скважины,

получим

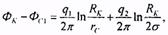
помещая ее на контур второй скважины, найдем

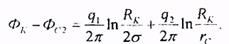
Так как скв. 1 полностью заглушена, то ее дебит q1=0 и уравнения приобретают вид

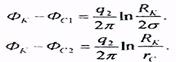
отсюда, исключая дебит q₂, определим потенциал Фc1:

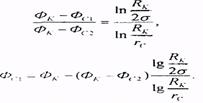
Переходя от потенциалов к давлениям, окончательно найдем

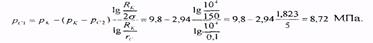
Задача 19

Определить дебиты скважин двух круговых батарей с радиусами

R1=1000м, R2=600м расположенных концентрично в круговом пласте с радиусом контура питания R_K=3500 м. Скважины радиусом r_г=10 см эксплуатируются при постоянных забойных давлениях рc1⁼9,8 МПа, Рсз=9,31 МПа, давление на контуре питания Рк⁼ 12,25 МПа, толщина пласта h= 10 м, коэффициент проницаемости пласта к=0,2 мкм²,динамический коэффициент вязкости нефти μ= 5 мПа*с. Число скважин в батареях m1=10, m2=6.

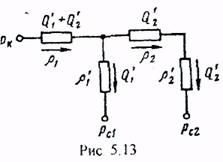
Решение.Используя метод Ю.П. Борисова, составим схему эквивалентных фильтрационных сопротивлений (рис.5.13).

Определим внешние и внутренние фильтрационные сопротивления:

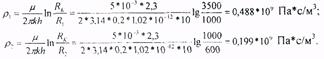
Для определения внутренних фильтрационных сопротивлений найдем половины расстояний между скважинами первой и второй батарей:

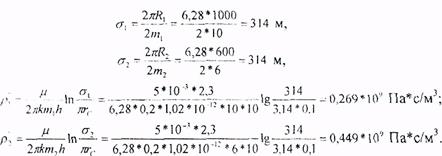
Используя законы Ома и Кирхгофа, напишем уравнение для участка цепи между контуром питания и забоем скважины первой батареи:

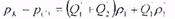
и аналогично между контуром питания и забоем скважины второй батареи:

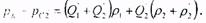
В полученнуюсистему уравнений подставим данные:

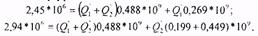
решая уравнения относительно Q1и Q2, найдем:

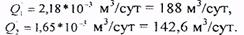
Учитывая, что Q1и Q2- суммарные дебиты первой и второй батарей, найдем дебиты одной скважины:

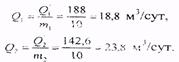
Задача 20

Определить дебиты скважин, расположенных тремя кольцевыми батареями. Давление на контуре питания рк=16,7 МПа, забойные давления на всех эксплуатационных скважинах одинаковы и равны рс1=рс2=рс3= 11,8 МПа. Радиусы батарей R₁=4000 м, R₂=3500 м, R₃=3000 м. Радиус скважин rc=0,1м, радиус контура области питания R_к=20 км. Расстояние между скважинами в батареях 2σ1=2σ2=2σ3=400 м, толщина пласта h=10 м, коэффициент проницаемости к=1 мкм², динамический коэффициент вязкости нефти μ=3 мПа*с.

Указание. Задачу решать методом эквивалентных фильтрационных сопротивлений Ю.П. Борисова.

Задача 21

Определить забойные давления скважин, расположенных в круговом пласте радиуса R_K =10 км двумя концентричными кольцевыми батареями с радиусами R1=2000 м., R2=1200 м. Число скважин к батареях m1=30,m2=16;

дебит одной скважины первой батареи Q₁=80 м³/сут, второй - Q₂~70 м³/сут; радиус скважины r_с=10 см, толщина пласта h=15 м, коэффициент проницаемости пласта k=0,8 мкм², динамический коэффициент вязкости жидкости μ=8 мПа*с, давление на контуре питания пласта р_к=14,7 МПа.

Задача 22

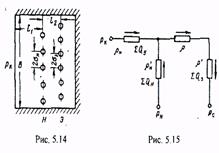
В полосообразной залежи имеется один ряд эксплуатационных и один ряд нагнетательных скважин, расположенный между контуром питания и эксплуатационными скважинами (рис.5.14).

Определить необходимое количество

жидкости 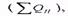, давление нагнетания р_н и утечку жидкости за контур питания 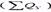(или количество поступающей жидкости от контура питания), чтобы суммарный дебит эксплуатационных скважин составлял ∑Q=1000 м³/сут. Ширина залежи равна В=5000 м, толщина пласта h=10 м, расстояние от контура питания до ряда нагнетательных скважин L1=1500 м, расстояние между рядами скважин L₂=600 м, расстояние между нагнетательными скважинами 2σп=300м, между эксплуатационными скважинами 2σэ=400 м; все скважины гидродинамически несовершенны, приведенный радиус составляет r_c ⁼0,1 см, давление на контуре питания рк= 11,76 МПа, давление па забое эксплуатационных скважин р_с=7,84 МПа, коэффициент проницаемости пласта k=0,5 мкм², динамический коэффициент вязкости нефти μ=4мПа*с.

Решение. Составим схему фильтрационных сопротивлений, отвечающую нашей задаче (рис.5.15), и найдем фильтрационные сопротивления, проводя расчет для суммарных дебитов рядов.

Внешние сопротивления равны:

- между контуром питания и нагнетательным рядом

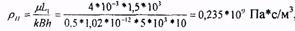
- между рядами скважин

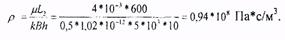
Для определения внутренних сопротивлений найдем число эксплуатационных (mэ) и нагнетательных (mн) скважин:

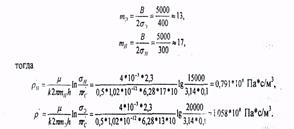
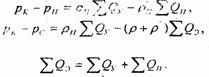Согласно законам Кирхгофа, считая, что жидкость поступает в пласт от контура, составим уравнения:

кроме того ,

Из второго уравнения находим

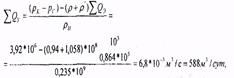
из третьего - закачиваемый дебит

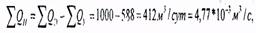
а из первого - давление нагнетания р_н

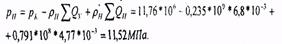
Так как ∑Qy, > 0 , то в действительности имеет место приток жидкости в пласт, а не утечка за контур питания.

Задача 23

Используя данные предыдущей задачи, определить давление нагнетания рн, количество нагнетаемой жидкости ∑Q и величину утечки за контур питания ∑Qy, если поменять местами ряды эксплуатационных и нагнетательных скважин (т.е. рассмотреть случай заводнения со стороны непроницаемой границы) и принять давление на контуре питания рк=9,8 МПа.